Как построить угол 30 градусов по клеточкам: Как отмерить угол 30 градусов на фанере без специальных инструментов?

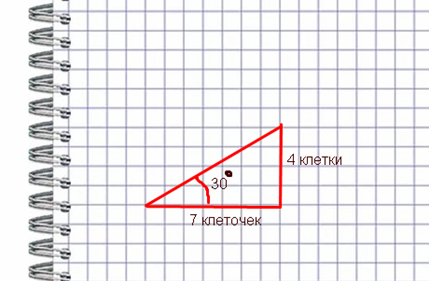
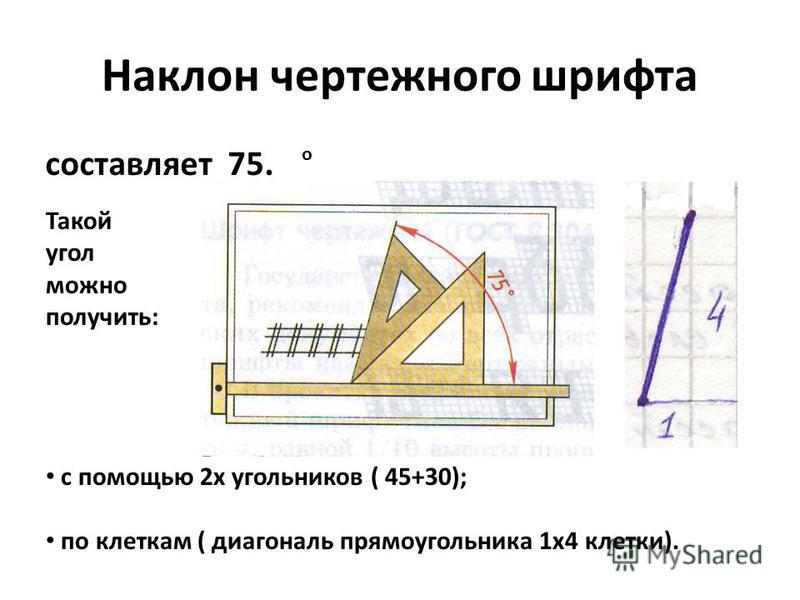
30 градусов по клеткам

Главная » Статьи » 30 градусов по клеткам

угол 30 градусов по клеточкам — Как построить угол в 30 градусов, без транспортира? — 22 ответа



В разделе Домашние задания на вопрос Как построить угол в 30 градусов, без транспортира? заданный автором разбросать лучший ответ это в воображаемом прямоугольнике с длиной 2 клетки и высотой 1 клетка провести диагональ.угол с большей стороной 30 градусов.

Ответ от Недосол[гуру]Вспомни про синусОтвет от Невроз[гуру]на тетради в клетку, от точки в сторону 5 клеток и 3 клетки вверхОтвет от VVVV[гуру]Оношение 3:5 К примеру три клеточки по вертикали пять по горизонтали… 🙂Ответ от Їахлык Невмерущий[гуру]Египетский треугольник = прямоугольный, стороны его равны 3,4, 5 частей. против меньшей стороны лежит угол в 30 гр. Следовательно сначала выбираем единицу = 1 части. Строим отрезки равные 3,4 и 5 частям. Соединием концы отрезков при помощи откладыванея циркулем от концов одной из сторонн получаем треугольник и угол в 30 градусов. Ответ от Daragoy igoriosha[гуру]Надо начертить (нарисовать) прямоугольный треугольник с катетами 3 и 5.Тогда, как известно, гипотенуза будет равна 6, т. к.3? + 5? = 6? (по теореме Пифагора)Острый угол будет = 30°так как его sin = отношению противолежащего катета к гипотенузе

sin 30° = 3 / 6 = 1 / 2

Ответ от Ёергей Веденских[новичек]я не понимаю гипотниузы всякие… я только в 5 классе

=(

Ответ от Алина савчишина[новичек]Как начертить угол 120 градусовОтвет от Annabella[активный]Блин, люди, что Вы советуете! Это же неправильно! Какие 1 и 2 клетки? Гипотенуза в этом случае равна корню из пяти! Ну как может корень из пяти быть равен 1?

Или тот же египетский треугольник со катетами 3 и 5? Гипотенуза в этом случае равна корню из 34, который тоже никак не равен 3!

Ответ от Иван Блинов[новичек]Меня в детстве учили тоже что 1 и 2 клетки. НЕ СЛУШАЙТЕ ИХ, Я СЕЙЧАС ЧУТЬ РАЗРЫВ МОЗГА НЕ ПОЛУЧИЛ КОГДА ОСОЗНАЛ, ЧТО ЭТО НЕПРАВДА. 1 И 2 КЛЕТКИ ЭТО ЛОЖЬ, ПРО 5 И 3 ТОЖЕ ОБМАН. ЭТИ ПРИБЛИЖЕНИЯ ДЛЯ МОЛОДОГО МОЗГА — ИГРУШКА ДЬЯВОЛА, ЕЖЖИ. Спасибо, я все

22oa.ru

Угол 30 градусов

Ключом к подобным «клетчатым» построениям углов является волшебное число 11. Если по клеткам нарисовать прямоугольный треугольник с одним катетом, равным 11 клеток, то выбор другого катета будет для этого треугольника давать следующие острые углы:

• 1 клетка — 5° и 85°
• 2 клетки — 10° и 80°
• 3 клетки — 15° и 75°
• 4 клетки — 20° и 70°
• 5 клеток — 25° и 65°

Запомнить нетрудно: каждая клетка добавляет по пять градусов, и так до пяти клеток. Погрешность составит около половины градуса для катетов 5 и 11 клеток, в остальных случаях она значительно меньше.

Ещё полезно помнить, что прямоугольный треугольник с катетами 8 и 11 клеток имеет острый угол 36° (с очень хорошей точностью). Это позволяет строить правильные пятиугольники и десятиугольники.

Волшебные свойства числа 11 на этом не заканчиваются. Выпишем последовательно натуральные числа: 3,4,5,6,7,8. Будем выбирать из них «крайние» пары: 3 и 8, 4 и 7, 5 и 6. Как видно, в сумме они все дают опять-таки 11. Если брать эти пары в качестве катетов, то получающиеся прямоугольные треугольники будут иметь следующие углы:

• 3 и 8 клеток — 20° и 70° (менее точно, чем для катетов 4 и 11 клеток)
• 4 и 7 клеток — 30° и 60°
• 5 и 6 — 40° и 50°

Ошибка составит около половины градуса для катетов 3 и 8 клеток, а в двух других случаях будет значительно меньше.

Отсюда следует способ построения по клеткам равностороннего треугольника: если взять горизонтальный или вертикальный отрезок 8 клеток и от его середины отступить в перпендикулярном направлении на 7 клеток, то получившийся равнобедренный треугольник будет практически равносторонним.

отмерить угол без транспортира

Ошибка очень мала: для стандартной 5-мм клетки основание будет равно 4 сантиметра, а боковая сторона отличается от этой величины всего на 0. 3 миллиметра. Это меньше, чем толщина карандашной линии.

Неплохо помнить ещё две пары катетов, дающих следующие острые углы:

• 2 и 9 клеток — 12° и 78°
• 1 и 10 клеток — 6° и 84°

Как видно, в сумме они составляют опять-таки 11. Наибольшая погрешность снова около половины градуса (у пары 2 и 9 клеток).

Эта клетчатая тригонометрия позволяет без проблем строить любые углы с шагом 5° без транспортира при неплохой точности.

Как построить угол в 30 градусов, без транспортира?

6. Как построить углы 30, 60, 90, 120, 150 градусов, циркулем?

Измерения и построение углов при проведении различных работ. Золотой египетский треугольник.

Как сложить бумагу для снежинки из 6 лучей (пошаговая инструкция)

Напротив угла в 30 градусов лежит катет равный половине гипотенузы

? АВС — равнодедренный, следовательно высота треугольника является и медианой и бессектриссой. Бессиктрисса ВД делит отрезок АС на 2 конгруэнтных отрезка. Расмотрим ? АВД. ? АВД прямоугольный , так как ВД перпендикулярно АС. Для то го чтобы найти 1 сторону прямоугольного треугольника.

Свойства прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, в которой один угол обязательно прямой. Треугольник с прямым углом имеет ряд свойств.

Основные свойства

Итак, свойства прямоугольного треугольника:

Первое и самое главное, прямой угол, благодаря которому он и получил свое название. Он, как известно, равен 90 градусам. Два остальных угла в сумме должны составлять также это значение. Таким образом, в обозначенной фигуре сумма всех углов должна составлять 180 градусов – это и есть свойства углов прямоугольного треугольника.

Второе, немаловажное свойство — это стороны прямоугольного треугольника: гипотенуза и два катета. Катет прямоугольного треугольника, что находится напротив угла в 30 градусов, равняется половине гипотенузы.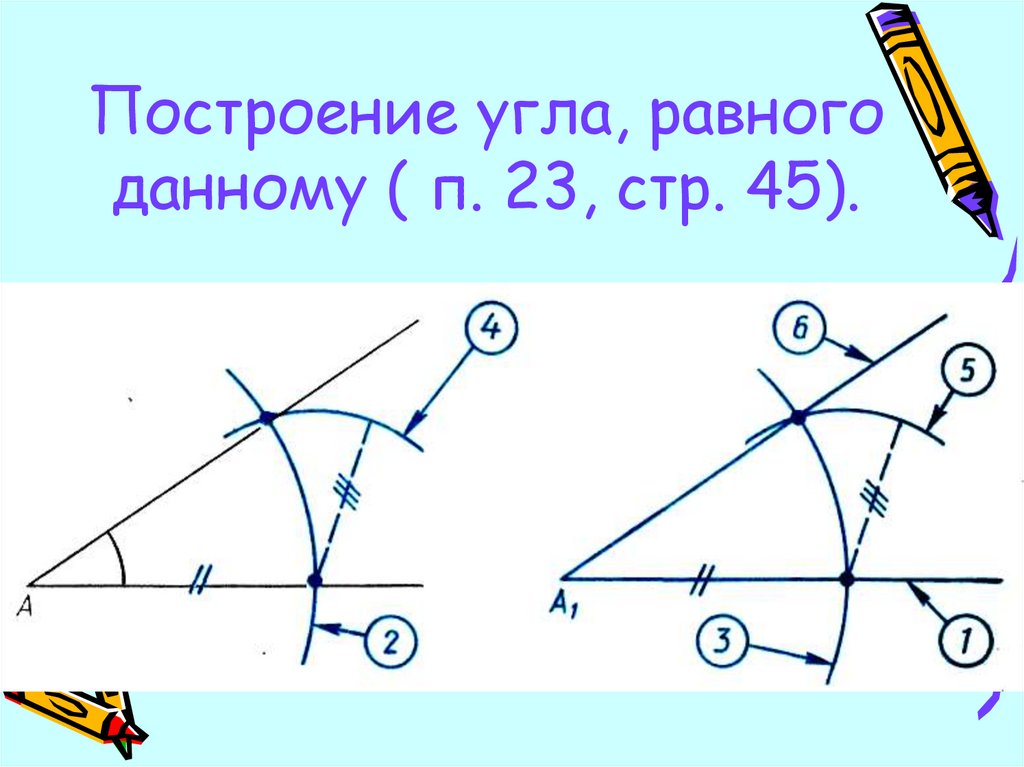

Теорема Пифагора

К свойствам прямоугольного треугольника относиться и теорема Пифагора: квадрат гипотенузы, равен суме квадратов катетов.

C 2 = a 2 + b 2 , где а и b – катеты, а с – гипотенуза.

Площадь прямоугольного треугольника равна половине произведения его катетов: S=1/2ab

Свойства медианы

Так же следует отметить и свойства медианы в прямоугольном треугольнике. Медианы, которые падают на гипотенузу, равны ее половине.

Если в прямоугольном треугольнике провести высоту с вершины, которая равна 90 о к гипотенузе, то треугольник делиться на два одинаковых прямоугольных треугольника. С этого можно сделать вывод, что высота в прямоугольном треугольнике, есть среднее геометрическое двух отрезков гипотенузы. Соответственно, каждый катет – среднее пропорциональное гипотенузы и смежных отрезков. Также нужно знать, что высота, которая опущена на гипотенузу, связана с катетами в соотношении: 1/а 2 + 1/b 2 = 1/f 2 , где а и b – катеты, а f –высота.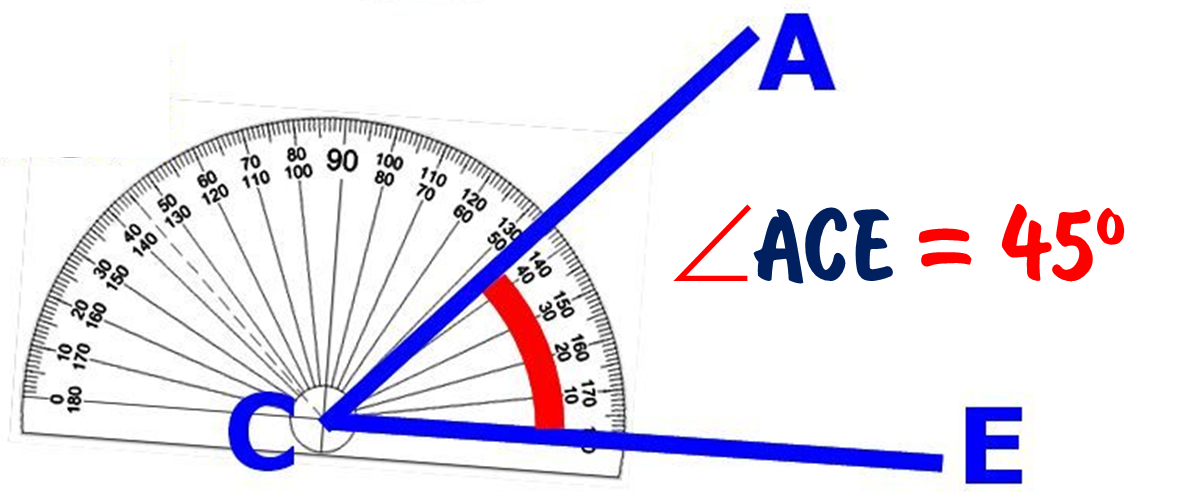

Напротив угла в 30 градусов лежит катет равный половине гипотенузы

Свойства прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, в которой один угол обязательно прямой. Треугольник с прямым углом имеет ряд свойств.

Основные свойства

Итак, свойства прямоугольного треугольника:

Первое и самое главное, прямой угол, благодаря которому он и получил свое название. Он, как известно, равен 90 градусам. Два остальных угла в сумме должны составлять также это значение. Таким образом, в обозначенной фигуре сумма всех углов должна составлять 180 градусов – это и есть свойства углов прямоугольного треугольника.

Второе, немаловажное свойство — это стороны прямоугольного треугольника: гипотенуза и два катета. Катет прямоугольного треугольника, что находится напротив угла в 30 градусов, равняется половине гипотенузы.

Теорема Пифагора

К свойствам прямоугольного треугольника относиться и теорема Пифагора: квадрат гипотенузы, равен суме квадратов катетов.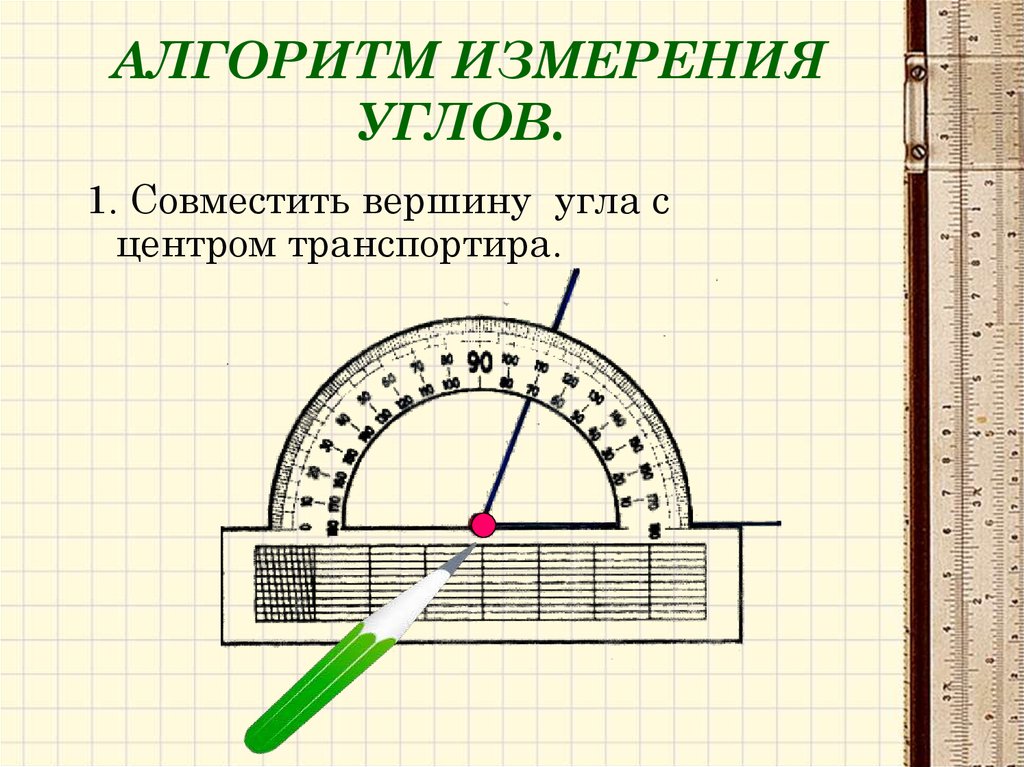

C 2 = a 2 + b 2 , где а и b – катеты, а с – гипотенуза.

Площадь прямоугольного треугольника равна половине произведения его катетов: S=1/2ab

Свойства медианы

Так же следует отметить и свойства медианы в прямоугольном треугольнике. Медианы, которые падают на гипотенузу, равны ее половине.

Если в прямоугольном треугольнике провести высоту с вершины, которая равна 90 о к гипотенузе, то треугольник делиться на два одинаковых прямоугольных треугольника. С этого можно сделать вывод, что высота в прямоугольном треугольнике, есть среднее геометрическое двух отрезков гипотенузы. Соответственно, каждый катет – среднее пропорциональное гипотенузы и смежных отрезков. Также нужно знать, что высота, которая опущена на гипотенузу, связана с катетами в соотношении: 1/а 2 + 1/b 2 = 1/f 2 , где а и b – катеты, а f –высота.

Напротив угла в 30 градусов лежит катет равный половине гипотенузы

Катет, лежащий против угла 30 градусов

Катет, лежащий против угла 30 градусов, равен половине гипотенузы.

Проведем из вершины прямого угла медиану CF.

Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.

Следовательно, у него углы при основании равны:

Так как сумма углов треугольника равна 180º, то в треугольнике BFC

Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.

Значит, все его стороны равны и

Что и требовалось доказать.

Так как сумма острых углов прямоугольного треугольника равна 90º, то

Построим треугольник ADC, равный треугольнику ABC.

В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).

Следовательно, в треугольнике ABD все углы равны:

Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.

shtyknozh.ru

Построение острых углов на клетчатой бумаге

Геометрия – часть математики, изучающая пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре. Происхождение термина «геометрия» с греческого означает «землемерие» [гео– «земля» и метрео – «измеряю»].

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Углы измеряются в градусах и радианах. Угол, образованный продолжением сторон данного угла, называется вертикальным к данному. Угол, образованный одной из сторон данного угла и продолжением другой стороны, называется смежным с ним. Приспособление для построения углов на чертежах, называется транспортир.

Значение геометрии в развитии математике

Применение евклидовой геометрии представляет самое обычное явление всюду, где определяются площади, объемы и т. п. Геометрия изучает пространственную непрерывность. Общая роль геометрии в математике состоит также в том, что с нею связано идущее от пространственных представлений точное синтетическое мышление, часто позволяющее охватить в целом то, что достигается анализом и выкладками лишь через длинную цепь шагов. Геометрия характеризуется не только своим предметом, но и методом, идущим от наглядных представлений и оказывающимся плодотворным в решении многих проблем других областей математики. Геометрия имела решающее значение в возникновении и развитии анализа. Интегрирование происходит от нахождения площадей и объемов. Графическое представление функций сыграло важную роль в выработке понятий анализа и сохраняет свое значение. Геометрия оказывает влияние на алгебру, и даже на арифметику – теорию чисел, поэтому роль геометрии в развитии математике очень велика.

Цель работы: найти способ построения углов без транспортира.

Гипотеза: Любой острый угол можно построить без транспортира по узлам клетки.

Задачи:

• рассмотреть углы и найти их связь с узлами клеток.

Построим с помощью транспортира углы от 10° до 80° со стороной, идущей по горизонтальной линии сетки.

Отметим у каждого угла ближайший узел сетки, через который прошла другая сторона каждого угла.

Определим «путь» из вершины угла в отмеченную точку и занесем данные в таблицу:

Величина угла Клеток → Клеток ↑

10° 6 1

20° 8 3

30° 7 4

40° 6 5

50° 5 6

60° 4 7

70° 3 8

80° 1 6

Если сравнить данные таблицы для углов 10° и 80°, 20° и 70°, 30° и 60°, 40° и 50°, то можно заметить, что количество клеток вправо и количество клеток вверх меняются местами.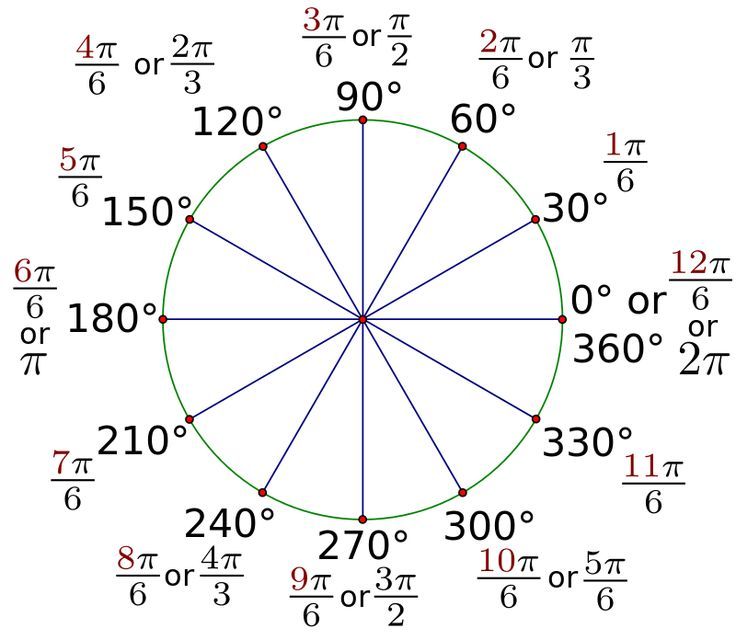

Используя данные таблицы, можно приближенно построить любой острый угол без транспортира.

Заключение

Таким образом, обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур. В 7 классе мы начинаем изучать геометрию и, полученными результатами, можно будет пользоваться при изучении курса планиметрии для построения схематических чертежей, точнее соответствующих условию задач.

Также, выполняя презентацию работы, я совершенствовала свои навыки работы на компьютере.

www.hintfox.com

Как построить угол в 30 градусов, без транспортира?

Как построить угол в 30 градусов, без транспортира?

на тетради в клетку, от точки в сторону 5 клеток и 3 клетки вверх

Оношение 3:5 К примеру три клеточки по вертикали пять по горизонтали.. . 🙂

Египетский треугольник = прямоугольный, стороны его равны 3,4, 5 частей. против меньшей стороны лежит угол в 30 гр. Следовательно сначала выбираем единицу = 1 части.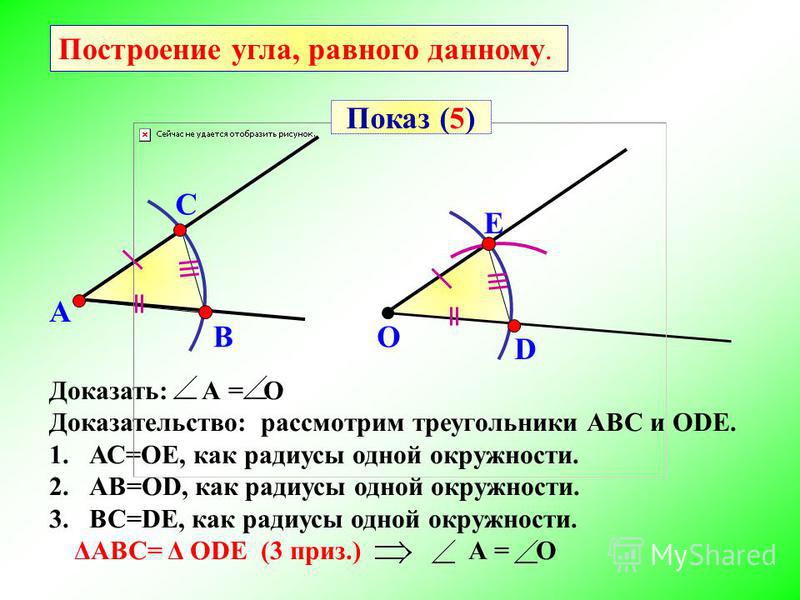 Строим отрезки равные 3,4 и 5 частям. Соединием концы отрезков при помощи откладыванея циркулем от концов одной из сторонн получаем треугольник и угол в 30 градусов.

Надо начертить (нарисовать) прямоугольный треугольник с катетами 3 и 5. Тогда, как известно, гипотенуза будет равна 6, т. к. 3² + 5² = 6² (по теореме Пифагора) Острый угол будет = 30° так как его sin = отношению противолежащего катета к гипотенузе sin 30° = 3 / 6 = 1 / 2

я не понимаю гипотниузы всякие… я только в 5 классе =(

Как начертить угол 120 градусов

Блин, люди, что Вы советуете! Это же неправильно! Какие 1 и 2 клетки? Гипотенуза в этом случае равна корню из пяти! Ну как может корень из пяти быть равен 1? Или тот же египетский треугольник со катетами 3 и 5? Гипотенуза в этом случае равна корню из 34, который тоже никак не равен 3!

Меня в детстве учили тоже что 1 и 2 клетки. НЕ СЛУШАЙТЕ ИХ, Я СЕЙЧАС ЧУТЬ РАЗРЫВ МОЗГА НЕ ПОЛУЧИЛ КОГДА ОСОЗНАЛ, ЧТО ЭТО НЕПРАВДА. 1 И 2 КЛЕТКИ ЭТО ЛОЖЬ, ПРО 5 И 3 ТОЖЕ ОБМАН. ЭТИ ПРИБЛИЖЕНИЯ ДЛЯ МОЛОДОГО МОЗГА — ИГРУШКА ДЬЯВОЛА, ЕЖЖИ. Спасибо, я все

Войдите, чтобы написать ответ

education.ques.ru

---

Смотрите также

• Крыша этапы строительства
• Как розу посадить в горшок
• Какое должно быть давление в системе отопления закрытого типа
• Как собирать сайдинг
• Перемычки в щитке для соединения автоматов какое сечение
• Поршневой компрессор устройство и принцип работы
• Как декор комнаты
• Что делать перед поклейкой обоев со стенами
• Если смешать коричневый и белый какой цвет получится
• Фурнитура на пластиковые окна
• Укрывной материал на зиму для растений как выбрать

 

Синус(sin), косинус(cos), тангенс(tg), котангенс(ctg) — как найти, отношение, формулы

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол

— больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ).

Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin	sincos
cos	1+tg	cos = sin
tg	1+ctg	sin = cos
ctg		tg = ctg

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на получаем то есть
   Мы получили основное тригонометрическое тождество.
4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

	0
sin	0
cos					0
tg	0				−
ctg	−				0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и и равными острыми углами А и

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому

Из этих равенств следует, что т. е. sin А = sin

Аналогично, т. е. cos А = cos и т. е. tg A = tg

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку , sin A = cos B = 0,1.

Задача 2. В треугольнике угол равен , , .

Найдите .

Решение:

Отсюда

Найдем AC по теореме Пифагора.

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A

Катет, прилежащий к – это катет АС, следовательно, cos⁡ А

Длину катета АС найдем по теореме Пифагора:

Тогда

cos⁡ А

tg A

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A

По теореме Пифагора получим

Ответ: 0,5.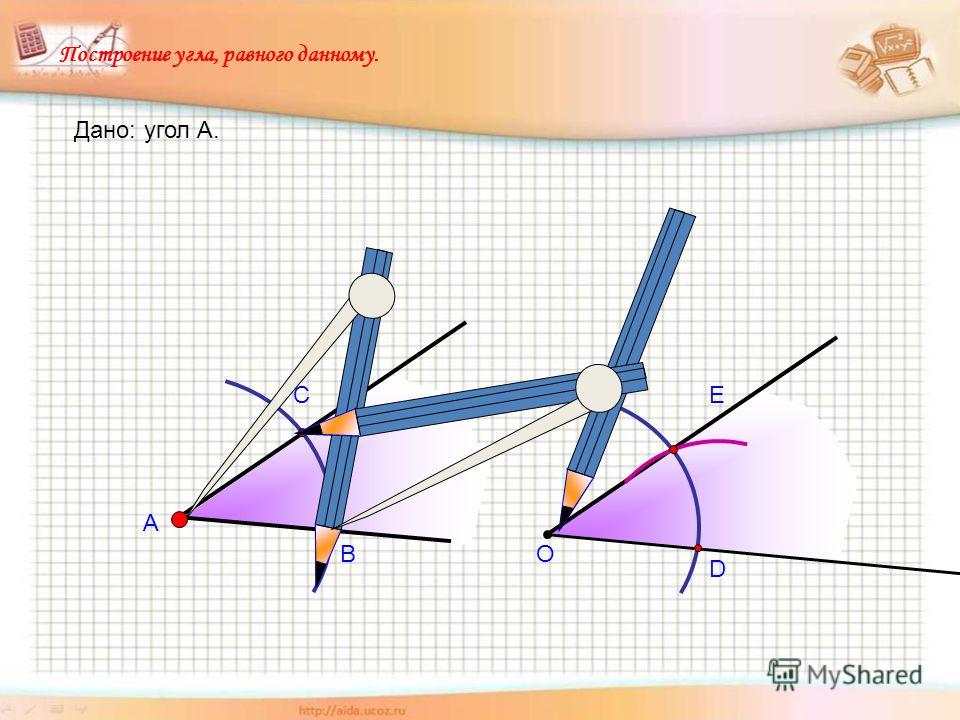

Задача 5. В треугольнике АВС угол С равен tg A = Найдите AB.

Решение:

AC = b = 4, tg A

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = Найдите AH.

Решение:

AВ = с = 13, tg A = тогда b = 5a.

По теореме Пифагора ABC:

тогда

(по двум углам), следовательно откуда

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A =

Найдите AH.

Решение:

Так как sin A = тогда c = АВ = 18.

sin A = = cos⁡ B =

Рассмотрим BHC:

= получим

тогда BH = = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =

Найдите АH.

Решение:

Так как для АВС: A = sin В =

а для ВНС: sin В = = , откуда СН =

По теореме Пифагора найдем ВН:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.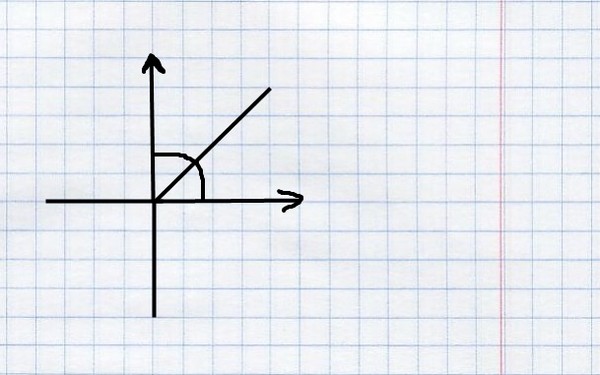 Поэтому для АВС получим:

тогда

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= = =

Рассмотрим BHC :

ВС найдем по теореме Пифагора:

ВС=

тогда а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = = = cos A = = =

тогда tg A = который найдем из BHC:

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A = Найдите АН.

Решение:

По определению tg A=

Для BHC: , значит СН =

Для АHC: tg A= то AH =

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A = Найдите АВ.

Решение:

Так как cos В = = sin A =

Из СВН имеем cos В = = тогда ВС =

В АВС имеем sinA = = тогда AВ =

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

sin В = =

Для АВС: cos A = получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора получим

х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит или

k = тогда АС = ; АВ =

3-й способ.

(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

=

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.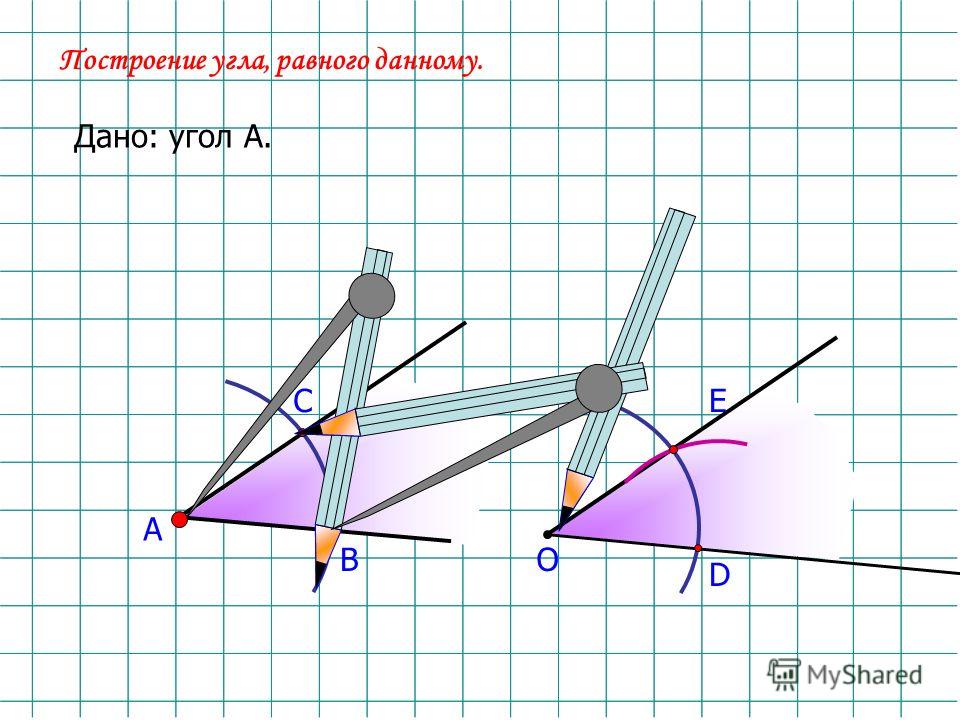

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = =

cos C =

Для АВС: sin А = = cos C =

Для АНВ: sin А = = то = АВ =

Из основного тригонометрического тождества найдем

cos A =

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А =

значит = 14.

Второй катет найдем, используя теорему Пифагора:

Площадь прямоугольного треугольника равна S =

поэтому

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, ),

значит sin

Найдем АС по теореме Пифагора из САВ:

Тогда sin

Ответ: 0,38.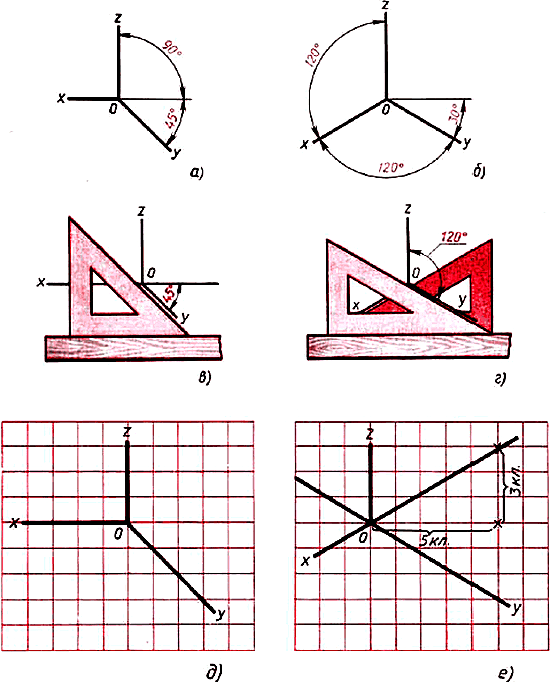

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ =

Поскольку АСН — прямоугольный,

cos A = то есть АС =

По теореме Пифагора тогда

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 sin A = AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора

(14х- 11х)(14х + 11х) = 3 100;

учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством

cos A =

По определению cos A = значит

Так как АС=10 то откуда АВ = = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.

Решение:

Пусть ВАО =

Диагонали ромба делят его углы пополам, значит, =

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =

Поэтому tg откуда

Ответ:

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 угол А равен 30 АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла имеем ВС = АВ =

В BHC: то следовательно, ВН = BC =

По теореме Пифагора найдем НС:

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 CH — высота, АВ = 2, Найдите АH.

Решение:

Из АВС найдем ВС = АВ = 1 (по свойству катета, лежащего против угла 30),

то

Из ВСН: то следовательно,

ВН = ВС =

АН = АВ — НВ = 2 — = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

 

Благодарим за то, что пользуйтесь нашими публикациями.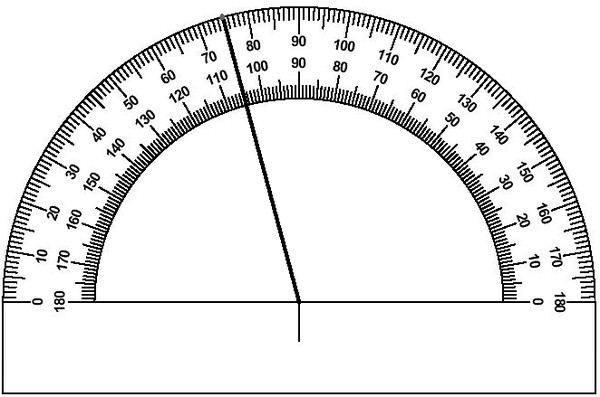 Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 25.12.2022

Угол 30 градусов – Этапы построения, Как измерить?, Примеры

LearnPracticeDownload

Угол 30 градусов является острым углом. Угол образуется, когда две линии встречаются или пересекаются в одной точке. Острый угол – это угол, градусная мера которого меньше 90 градусов. Разделив пополам угол в 60 градусов, мы получим два угла по 30 градусов каждый. Давайте узнаем об угле 30 градусов, этапах построения и некоторых реальных примерах 30 градусов.

1.	Что такое угол 30 градусов?
2.	Построение угла 30 градусов с помощью транспортира
3.	Построение угла 30 градусов с помощью компаса
4.	Углы 30 градусов в реальной жизни
5.	Часто задаваемые вопросы об угле 30 градусов

Что такое угол 30 градусов?

Угол образуется, когда два луча встречаются в одной точке. На данном рисунке точкой пересечения луча ОА и луча ОВ является точка О, которая называется вершиной.

Если угол, образованный двумя лучами, равен 30 градусам, то такой угол называется 30-градусным. Угол, образованный лучами OA и OB, записывается как ∠AOB или ∠BOA.

∠AOB=∠BOA=30°.

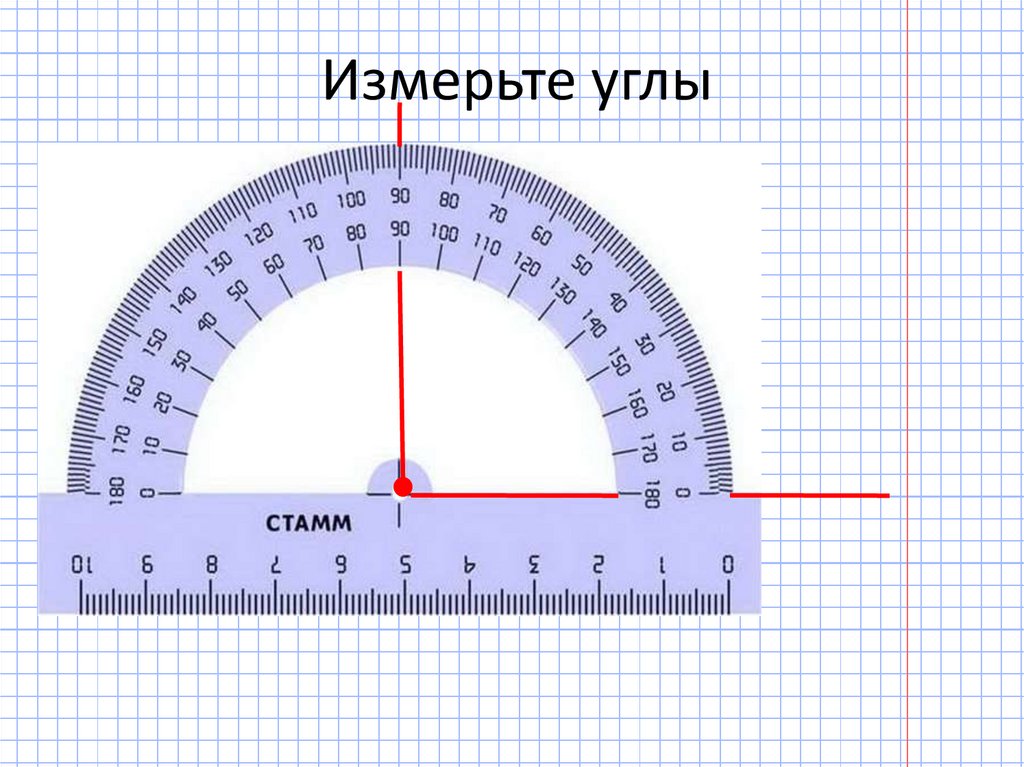
Построение угла 30 градусов с помощью транспортира

В этом разделе мы рассмотрим, как построить угол в 30 градусов с помощью транспортира. Выполните указанные шаги:

Шаг 1: Нарисуйте отрезок OA.

Шаг 2: Поместите центральный конец транспортира в точку O так, чтобы транспортир точно совпадал с линией AO.

Шаг 3: Начните с ‘A’ на транспортире по часовой стрелке и остановитесь на 30. Отметьте его как точку ‘D’. Если точка «А» лежит правее «О», то начните измерение против часовой стрелки и остановитесь на 30.

Шаг 4: Соедините точку «D» с «O». ∠AOD=30° — требуемый угол в 30 градусов.

Построение 30 градусов с помощью компаса

Угол в 30 градусов также можно построить с помощью компаса. Теперь давайте посмотрим, как построить угол в 30 градусов с помощью циркуля, линейки и карандаша. Следуйте инструкциям ниже:

• Нарисуйте луч AB. С центром А и подходящим радиусом на компасе начертите полуокружность так, чтобы она касалась отрезка АВ в точке С.
• С точкой C в центре и без изменения радиуса нарисуйте дугу, пересекающую дугу полукруга в точке D.
• С центрами C и D нарисуйте две пересекающиеся дуги и обозначьте их как E.
• Соедините точки A и E. Здесь ∠EAB = 30°.

Ниже показано построение угла 30° с помощью компаса.

30-градусные углы в реальной жизни

Угол в 30 градусов можно увидеть во многих окружающих нас объектах. Стрелки аналоговых часов в 1:00 образуют угол 30 градусов.

Пицца, разрезанная на 12 кусков, иногда образует угол в 30 градусов. Иногда ножницы, которыми мы режем бумагу и ткань, образуют угол в 30 градусов. Вы когда-нибудь катались на велосипеде с друзьями и замечали, что дороги расходятся под некоторыми углами. Эти углы могут быть углами в 30 градусов.

Think Tank

Проверьте несколько интересных вопросов об угле 30 градусов.

Сколько 30-градусных углов в

а) Прямой угол
b) Полный угол

Важные примечания

Вот несколько важных примечаний об угле 30 градусов.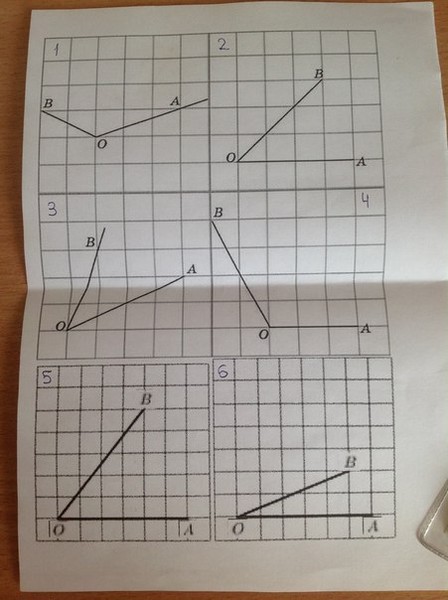

• Еще одной единицей измерения углов является радиан.
• π радиан = 180°.
• 30° в радианах равно π/6.
• Угол 30 градусов является острым углом.

Темы, связанные с углом 30 градусов

Ознакомьтесь с некоторыми интересными статьями, связанными с углом 30 градусов.

• Уголки
• Острый угол
• Тупой угол
• Типы углов
• Геометрия

 

Примеры углов 30 градусов

1. Пример 1: В △ABC используйте транспортир для измерения ∠CAB.

   Решение:

   Поместите базовую линию транспортира вдоль линии AB и центр транспортира в вершине A. Обратите внимание на показания транспортира, которые перекрываются с линией AC. Получается угол 30 градусов.

   Следовательно, ∠CAB=30°.

2. Пример 2: Мэтью заказал себе домой большую пиццу. Через некоторое время к нему домой пришли несколько его друзей. Мэтью позвонил в пиццерию и попросил их нарезать пиццу так, чтобы он получил 25% пиццы, а каждый из его друзей получил кусок под углом 30 градусов. Если каждый друг получил по кусочку, сколько друзей пришло к Мэтью?

   Решение:

   Пицца круглая; следовательно, центральный угол пиццы равен 360°.

   Мэтью съедает 25% пиццы.

   = 25% от 360°
   =(25/100)×360º
   =(1/4) × 360º = 90º
   Мэтью ест кусок, угол которого равен 90°.

   Оставшаяся пицца будет поровну распределена между его друзьями.

   360° — 90° = 270°

   Теперь друзья Мэтью будут есть пиццу 270°. Каждый кусочек пиццы имеет угол 30 градусов. Следовательно, общее количество друзей, пришедших в дом Мэтью, равно 9.0003

   Общий угол остатка пиццы/Угол каждого ломтика
   = 270/30
   = 9
   Поэтому в дом Мэтью пришли 9 друзей.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по углу 30 градусов

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле 30 градусов

Какой тип угла составляет угол 30 градусов?

Угол в 30 градусов является острым, поскольку он меньше 90 градусов.

Как нарисовать угол 30 градусов с помощью транспортира?

Чтобы нарисовать угол в 30 градусов с помощью транспортира, выполните следующие действия:

• Шаг 1: Нарисуйте отрезок OA.
• Шаг 2: Поместите центральный наконечник транспортира в точку A так, чтобы транспортир точно совпадал с линией AO.
• Шаг 3: Начните с 0 на транспортире по часовой стрелке и остановитесь на 30. Отметьте точку D.
• Шаг 4: Соедините точку D с точкой A. Требуемый угол ∠DAO=30°.

Сколько углов в 30 градусов нужно, чтобы сделать полный оборот?

Полный оборот составляет 360°. Поскольку 30 × 12 = 360, следовательно, в полном обороте двенадцать углов по 30 градусов.

Сколько 30-градусных углов в треугольнике 30-60-90?

Треугольник 30-60-90 — это треугольник, в котором один из углов равен 30 градусам. Два других угла равны 60 и 90 градусов каждый. Итак, в треугольнике 30-60-90 есть только один угол в 30 градусов.

Сколько 30-градусных углов содержится в прямом и полном углах?

Прямой угол, равный 180°, содержит шесть 30° углов. Это вычисляется путем деления 180° на 30°. Аналогично, в полном угле двенадцать углы 30°. Это рассчитывается путем деления 360° на 30°.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочие листы под углом 30 градусов

Рабочие листы по математике и
наглядная программа

Как наклонить и повернуть текст в Microsoft Excel

В Microsoft Excel вы можете поворачивать текст, наклонять его или отображать вертикально . Вот как можно изменить ориентацию текста на листе.

Будь то внешний вид или пространство, вы можете легко поворачивать текст в Excel. У вас есть простые способы наклонить его, заставить его отображаться вертикально или повернуть его вверх или вниз. И если у вас есть точная настройка, которую вы хотите использовать, вы можете настроить текст, используя точное количество градусов.

Здесь мы покажем вам, как использовать эти настройки для отображения текста в Microsoft Excel в соответствии с вашими предпочтениями.

Как повернуть текст под углом в Excel

Использование угла для текста может быть визуально приятным, особенно для заголовков столбцов и строк. Вы можете быстро повернуть текст на угол против или по часовой стрелке.

1. Выберите ячейки, содержащие текст, который вы хотите наклонить. Это может быть столбец, строка, ячейка или диапазон ячеек.
2. Перейти к 9Вкладка 0051 Home и нажмите кнопку Orientation в разделе ленты «Выравнивание».
3. Выберите один из двух верхних вариантов для Угол против часовой стрелки или Угол по часовой стрелке .

Затем вы увидите, что ваш лист немедленно обновляется с новым выровненным текстом. На скриншоте ниже мы повернули заголовки столбцов по часовой стрелке.

Как отобразить текст вертикально в Excel

Отображение текста вертикально может быть не часто используемой ориентацией, но может быть полезно в определенных обстоятельствах. Это может быть полезно, если вы используете заголовки строк, которые охватывают несколько строк. При желании вы можете объединить ячейки, а затем применить выравнивание; мы покажем вам, как сделать и то, и другое.

Объединить ячейки

1. Выберите ячейки, которые вы хотите объединить.
2. Перейдите на вкладку Главная и нажмите кнопку Объединить в разделе ленты «Выравнивание».
3. Выберите Объединить и центрировать или Объединить ячейки по своему усмотрению.

Текст в группе ячеек теперь находится в одной ячейке.

Применить выравнивание

1. Выберите ячейки, содержащие текст, который вы хотите отобразить вертикально.
2. Перейдите на вкладку Главная и нажмите кнопку Ориентация .
3. Выберите Вертикальный текст .

Ваша объединенная ячейка будет отображать текст или символы вертикально. Это помещает символы друг под другом и может быть прочитано сверху вниз.

Как повернуть текст вверх или вниз в Excel

Возможно, вам нравится вертикальное выравнивание, но вы не хотите, чтобы символы отображались сверху вниз. Вы можете повернуть текст вверх или вниз, чтобы читать сбоку. Это также полезно, если вы используете объединенные ячейки. Поэтому следуйте инструкциям выше, если вы хотите сначала объединить свои ячейки. Затем выполните следующие действия, чтобы применить выравнивание.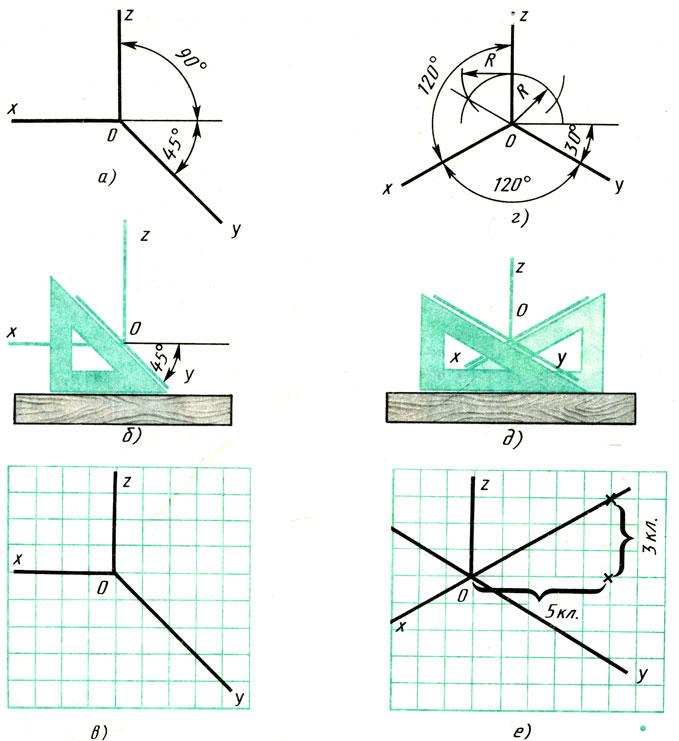

1. Выберите ячейки, содержащие текст, который вы хотите повернуть.
2. Перейдите на вкладку Главная и нажмите кнопку Ориентация .
3. Выберите Повернуть текст вверх или Повернуть текст вниз по своему усмотрению.

И, как и в случае с другими настройками выравнивания, вы увидите, что ваши ячейки обновляются с новым макетом.

Как повернуть текст, используя точные градусы в Excel

Когда вы применяете любую из вышеперечисленных ориентаций к тексту, вы также можете использовать точное количество градусов. Это может помочь вам получить правильный угол или интервал для текста. Вы также можете использовать следующую функцию с самого начала, а не выполнять предыдущие шаги, если хотите.

В этом примере мы собираемся настроить текст там, где мы применили ориентацию «Выровнять по часовой стрелке». Мы хотим немного уменьшить угол.

1. Выберите ячейки, содержащие текст, который вы хотите настроить.