Вес мальчиков по годам таблица: сколько должны весить мальчики и девочки по годам

средний вес 12-летнего ребенка

AlleBilderShoppingNewsMapsVideosBücher

suchoptionen

Средний вес 12-летнего ребенка составляет 89 фунтов для мальчиков и 92 фунта для девочек. Однако, помимо биологического пола, на вес человека в этом возрасте влияют многие другие факторы, в том числе рост, состав тела, начало полового созревания, факторы окружающей среды и основные проблемы со здоровьем.

_{24 сентября 2020 г.}

Каков средний вес 12-летнего ребенка? — Медицинские новости сегодня

www.medicalnewstoday.com › статьи › каков средний вес 1…

Hervorgehobene Snippets

Ähnliche Fragen

Какой нормальный вес для 12-летнего ребенка?

Что такое лишний вес для 12-летнего ребенка?

Каков средний вес 12-летнего ребенка? — Healthline

www.healthline.com › Темы о здоровье › Фитнес

13.06.2019 · CDC также сообщает, что вес 12-летней девочки обычно составляет от 68 до 135 фунтов, а вес 50-го процентиля для . ..

Девочка · Факторы · Здоровое питание · Резюме

Каков средний вес 12-летних мальчиков и девочек? — Hoodmwr

www.hoodmwr.com › … › Вес и рост

18.06.2022 · У детей с ожирением ИМТ равен или намного выше 95-го процентиля, в то время как у подростков с избыточным весом обычно ИМТ составляет от 85 до 95 процентиль …

Каков средний вес 12-летнего ребенка? — Quora

www.quora.com › Какой-средний-вес-для-12-летнего

По данным Google, средний вес 12-летней девочки составляет 93 фунта, мальчика — 90 фунтов. Как и в случае любого среднего показателя, здесь играет роль множество факторов. Какой рост у ребенка?

Каков нормальный вес 12-летней девочки с … — Quora

Каков средний вес 12-летнего мальчика ростом 5 футов 3 дюйма? — Quora

Каков средний вес 12-летнего ребенка ростом 4’11-5’0 футов? — Quora

Сколько должен весить 12-летний ребенок? Потому что я чувствую себя толстой. или . ..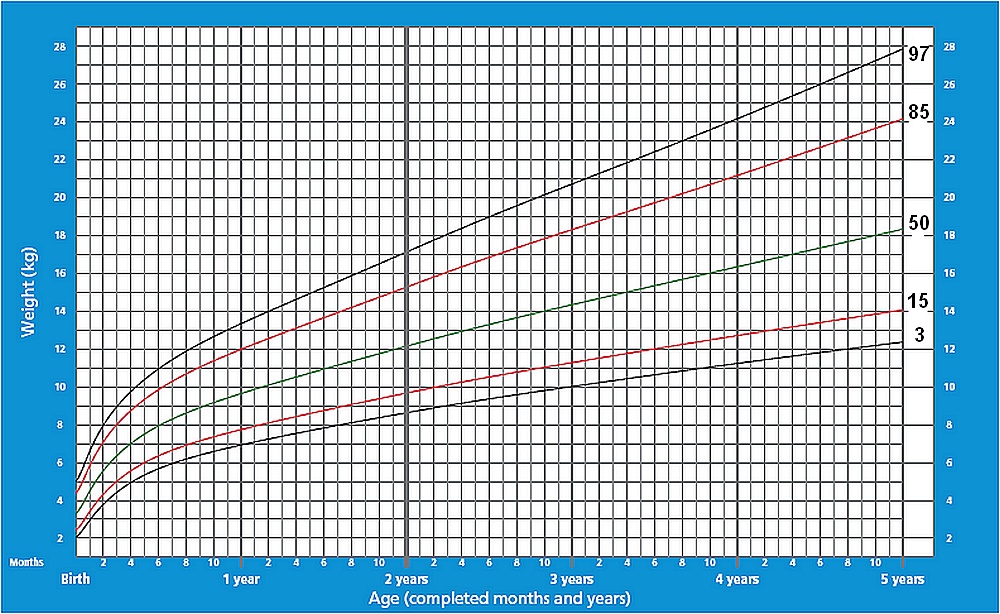

Weitere Ergebnisse von www.quora.com

Таблица среднего роста и веса: от младенцев до подростков

www.disabled-world.com Вес для детей женского пола — от 2 до 12 лет. Десятилетняя девочка будет весить в среднем около 70,5 фунтов (31,9 кг) …

Какой нормальный вес для 12-летнего ребенка? — Fueling Teens

www.fuelingteens.com › нормальный вес для 12 лет

Например, 12-летний мальчик ростом 58 дюймов (4 фута 10 дюймов) будет считаться «нормальным» или здоровым весом от 72 до 100 фунтов (от 33 до 45 кг) …

Что такое Здоровый вес для двенадцатилетних девочек?

healtheating.sfgate.com › … › Планирование питания

Дети с избыточным весом находятся между 85-м и 95-м процентилями, а дети с ожирением имеют ИМТ, равный или превышающий 95-й процентиль. Здоровый вес для …

Средний вес и рост для 12-летнего ребенка — Healthfully

Healthfully.com › the-average-weight-and-health-fo. ..

Средний рост — 50-й процентиль — для 12-летнего -летняя девочка ростом 59 дюймов и средним весом 93 фунта, по данным Центра болезней …

Средний рост и вес — Proxim

www.groupeproxim.ca › статья › здоровье › среднее-h …

Следующая таблица содержит средние значения роста и веса в зависимости от пола и возраста. Средний рост и вес в зависимости от возраста. Мужской женский. Возраст (год) … 

Каков средний вес 12-летнего ребенка? — Здоровье вашего организма

prirucnik.hr › koja-je-prosjecna-tezina-za-12-godisn…

26.06.2020 · Средний вес 12-летней девочки … Девочки в возраст 12 лет чаще всего приходится на диапазон от 68 до 135 кг, при этом 92 кг приходится на возраст 50 …

Ähnlichesuchanfragen

-старый весит

Какой средний вес 13-летнего ребенка в кг

Средний рост 12-летнего ребенка

Сколько должен весить 11-летний ребенок

Средний рост 13-летней девочки

Средний рост 13-летнего ребенка

Калькулятор ИМТ

Раздел 7.

2: Применение нормы Распределение

Задачи

К концу этого урока вы сможете…

1. найти и интерпретировать площадь под кривой нормали
2. найти значение нормальной случайной величины

Для быстрого ознакомления с этим разделом посмотрите этот краткий видеообзор. (Обратите внимание, что это то же самое видео для раздела 7.1, если вы уже смотрели его.)

Поиск площадей с помощью таблицы как найти площадь под кривой. Мы будем учиться двумя разными способами — с помощью таблицы и с помощью технологии.

Поскольку каждая нормально распределенная случайная величина имеет несколько иную форму распределения, единственный способ найти площади с помощью таблицы — это стандартизировать переменную — преобразовать нашу переменную так, чтобы она имела среднее значение 0 и стандартное отклонение 1.

Как мы это делаем? Используйте z-счет!

Z =	х — мк
	о

Как мы отмечали в разделе 7.1, если случайная величина X имеет среднее значение μ и стандартное отклонение σ, то преобразование X с использованием z-показателя создает случайную величину со средним значением 0 и стандартным отклонением 1! Имея это в виду, нам просто нужно научиться находить области под стандартная нормальная кривая , которую затем можно применить к любой нормально распределенной случайной величине.

Поиск площади под стандартной кривой нормали слева

Прежде чем мы рассмотрим несколько примеров, нам нужно сначала увидеть, как работает таблица. Прежде чем мы начнем раздел, вам нужна копия таблицы. Вы можете скачать распечатанную копию этой таблицы или использовать таблицу в конце учебника. Это должно выглядеть примерно так:

Сначала это довольно сложно, но если вы посмотрите на картинку вверху (найдите минутку и проверьте ее), вы увидите, что она указывает на область слева. Это ключ — значения в середине представляют области слева от соответствующего значения z. Чтобы определить, к какому z-значению оно относится, мы смотрим влево, чтобы получить первые две цифры, и выше к столбцам, чтобы получить значение сотых. (Значения Z с большей точностью необходимо округлить до сотых, чтобы использовать эту таблицу.)

Скажем, мы ищем область слева от -2,84. Для этого мы начнем со строки -2,8 и пройдемся, пока не дойдем до столбца 0,04. (См. рисунок.)

Из рисунка видно, что площадь слева от -2,84 равна 0,0023.

Поиск областей с помощью StatCrunch

Щелкните Стат. > Калькуляторы > Обычный Введите среднее значение, стандартное отклонение, x и направление неравенства. Затем нажмите Вычислить. На изображении ниже показано P (Z < 1,23).

Давайте попробуем несколько примеров.

Пример 1

а. Найдите площадь слева от Z = -0,72

[раскрыть ответ]

Площадь слева от -0,72 примерно равна 0,2358 .

б. Найдите площадь слева от Z = 1,90

[указать ответ]

Площадь слева от 1,90 примерно равна 0,9713 .

Нахождение площади под стандартной нормальной кривой вправо

Чтобы найти области справа, нам нужно помнить правило дополнения. Уделите минутку и вернитесь к правилу из Раздела 5.2.

Поскольку мы знаем, что вся площадь равна 1,

(Площадь справа от z ₀ ) = 1 — (Площадь слева от z ₀ )

Пример 2

a. Найдите площадь справа от Z = -0,72

[раскрыть ответ]

площадь справа от -0,72	=	1 — (область слева от -0,72)
	=	1 — 0,2358
	=	0,7642

б. Найдите площадь справа от Z = 2,68

[укажите ответ]

площадь справа 2,68	=	1 — (площадь слева от 2,68)
	=	1 — 0,9963
	=	0,0037

Альтернативная идея заключается в использовании свойства симметрии нормальной кривой. Вместо того, чтобы смотреть вправо от Z=2,68 в примере 2 выше, мы могли бы посмотреть на область слева от -2,68 . Поскольку кривая симметрична, эти области одинаковы.

Нахождение площади под стандартной нормальной кривой между двумя значениями

Чтобы найти площадь между двумя значениями, мы разделяем ее на две части. Предположим, мы хотим найти площадь между Z = -2,43 и Z = 1,81.

Вместо этого мы найдем площадь, оставшуюся от 1,81, а затем вычтем площадь, оставшуюся от -2,43.

Вот так:

Таким образом, площадь между -2,43 и 1,81 = 0,9649 — 0,0075 = 0,9574

Примечание: StatCrunch может рассчитать «между» вероятностями, так что вы не будете необходимо выполнить приведенный выше расчет, если вы используете StatCrunch.

Пример 3

а. Найдите площадь между Z = 0,23 и Z = 1,64. б. Найдите площадь между Z = -3,5 и Z = -3,0.

[раскрыть ответ]

область между -3,5 и -3,0 = 0,0013 — 0,0002 = 0,0011

Поиск площадей под нормальной кривой с помощью таблицы

1. Нарисуйте эскиз нормальной кривой и заштрихуйте нужную область.
2. Рассчитайте соответствующие Z-показатели.
3. Найдите соответствующую площадь под стандартной кривой нормали.

Если вы помните, это именно то, что мы видели на демонстрации в области нормального распределения. Перейдите по ссылке и снова изучите взаимосвязь между площадью под стандартной нормальной кривой и нестандартной нормальной кривой.

Поиск областей под кривой нормали с помощью StatCrunch

Несмотря на то, что здесь нет «стандарта» в заголовке, направления на самом деле точно такие же, как и выше!

Щелкните Стат. > Калькуляторы > Обычный Введите среднее значение, стандартное отклонение, x и направление неравенства. Затем нажмите Вычислить. На изображении ниже показано P (Z < 1,23).

Теперь мы, наконец, добрались до настоящей причины, по которой мы изучаем нормальное распределение. Мы хотим иметь возможность отвечать на вопросы о переменных, которые имеют нормальное распределение. Вопросы типа…

• Какая доля людей являются гениями?
• Является ли систолическое артериальное давление 110 необычным?
• Какой процент лампочек определенной марки излучает от 300 до 400 люмен?
• Каков 90-й процентиль веса годовалых мальчиков?

На все эти вопросы можно ответить, используя нормальное распределение!

Пример 4

Давайте снова рассмотрим распределение IQ, которое мы рассматривали в примере 1 в разделе 7. 1.

В этом примере мы видели, что тесты на коэффициент интеллекта (IQ) человека предназначены для нормального распределения со средним значением 100 и стандартным отклонением 15.

16 января психолог Льюис М. Турман установил ориентир в 140 баллов (в сегодняшних тестах он был увеличен до 136) для «потенциального гения».

Используя эту информацию, какой процент людей является «потенциальными гениями»?

Решение:

1. Нарисуйте набросок кривой нормали и заштрихуйте нужную область.
   
2. Рассчитайте соответствующие Z-показатели.
   

   Z =	Х — мк	=	136 — 100	= 2,4
   	о		15

3. Найдите соответствующую площадь под стандартной кривой нормали.
   P(Z>2,4) = P(Z<-2,4) = 0,0082.

Исходя из этого, получается, что около 0,82% людей могут быть охарактеризованы как «потенциальные гении» по критериям доктора Турмана.

Пример 5

Источник: stock.xchng

В примере 2 в разделе 7.1 нам сказали, что вес годовалых мальчиков распределен приблизительно нормально, со средним значением 22,8 фунта и стандартным отклонением около 2,15. (Источник: About.com)

Если мы случайным образом выберем годовалого мальчика, какова вероятность того, что он будет весить не менее 20 фунтов?

Решение:

Давайте сделаем это с помощью технологий. Начать все же следует с наброска:

Используя StatCrunch, мы получаем следующий результат:

Согласно этим результатам вероятность того, что случайно выбранный годовалый мальчик будет весить более 20 фунтов, составляет около 0,9036.

Почему бы тебе не попробовать парочку?

Пример 6

Фото: A Syed

Предположим, что объем краски в 1-галлонных банках с краской производства Acme Paint Company приблизительно нормально распределен со средним значением 1,04 галлона и стандартным отклонением 0,023 галлона.

Какова вероятность того, что случайно выбранная 1-галлонная банка на самом деле будет содержать по крайней мере 1 галлон краски?

[ раскрыть ответ ]

В этом случае мы хотим P(X ≥ 1). Снова воспользовавшись StatCrunch, получаем следующий результат:

Согласно расчетам, вероятность того, что в случайно выбранной банке окажется больше 1 галлона, составляет примерно 0,9590.

Пример 7

Предположим, что количество света (в люменах), излучаемого определенной маркой лампочек мощностью 40 Вт, нормально распределено со средним значением 450 люмен и стандартным отклонением 20 люмен.

Какой процент ламп излучает от 425 до 475 люмен?

[ раскрыть ответ ]

Чтобы ответить на этот вопрос, нам нужно знать:
P(425 < X < 475)

Чтобы использовать StatCrunch, нам нужно найти вероятность быть меньше 425, а затем вычесть это из вероятности быть меньше 475:

P(X<425) :

P(X<475):

Итак, P(425 < X < 475) = 0,8944 - 0,1056 = 0,7888

Таким образом, процент излучения от 425 до 475 люмен составляет около 79%.

 

Поиск значений

Следующий тип вопросов исходит из другого направления. Вместо того, чтобы давать значения и спрашивать вероятность, мы теперь будем рассматривать задачи, где вероятность известна, а значения нет. Например, такие вопросы:

• Каков 90-й процентиль веса годовалых мальчиков?
• Какой показатель IQ ниже 80% всех показателей IQ?
• Какой вес должен быть у годовалого мальчика, чтобы все, кроме 5% годовалых мальчиков, весили меньше, чем он?

Как и в предыдущих типах задач, мы научимся делать это, используя как таблицу, так и технологию. Убедитесь, что вы знаете оба метода — они оба используются во многих областях науки!

Нахождение Z-показателей с помощью таблицы

Идея здесь в том, что значения в таблице представляют площадь слева, поэтому, если нас попросят найти значение с площадью 0,02 слева, мы ищем 0,02 на внутри таблицы и найдите соответствующий Z-счет.

Поскольку у нас нет площади в точности 0,02, нам нужно немного подумать. У нас есть два варианта: (1) взять ближайшую область или (2) усреднить два значения, если они равноудалены от двух областей.

В данном случае они почти равноудалены, поэтому мы возьмем среднее значение и скажем, что Z-значение, соответствующее этой области, равно среднему значению -2,05 и -2,06, поэтому -2,055 .

Определение Z-показателей с помощью StatCrunch

Щелкните Стат. > Калькуляторы > Обычный Введите среднее значение, стандартное отклонение, направление неравенства и вероятность (оставьте X пустым). Затем нажмите Вычислить. На изображении ниже показана Z-оценка с площадью 0,05 вправо.

Давайте попробуем несколько!

Пример 8

а. Найдите Z-показатель с площадью 0,9.0 влево.

[ раскрыть ответ ]

Используя обычный калькулятор в StatCrunch, мы получаем следующий результат:

Таким образом, Z-показатель с площадью 0,90 слева равен 1,28 . (Обычно мы округляем Z-значения до сотых.)

b. Найдите Z-показатель с площадью 0,10 вправо.

[ раскрыть ответ ]

Фактически это то же значение, что и в примере 7 выше! Площадь 0,10 вправо означает, что она должна иметь площадь 0,90 влево, поэтому ответ снова 1,28 .

в. Найдите такой Z-показатель, что P(Z < z ₀ ) = 0,025.

[ раскрыть ответ ]

Используя StatCrunch, мы получаем следующий результат:

Таким образом, Z-показатель равен -1,96 .

Итак, мы поговорили о том, как найти z-показатель по площади. Если вы помните, в технологических инструкциях не указывалось, что дистрибутив должен быть стандартным нормальным — мы на самом деле находим значения в любое нормальное распределение , которое соответствует заданной области/вероятности с использованием тех же методов.

Пример 9

Снова обратимся к показателям IQ со средним значением 100 и стандартным отклонением 15. Найдите 90-й процентиль для показателей IQ.

Решение:

Во-первых, нам нужно перевести проблему в область или вероятность. В разделе 3.4 мы сказали, что k -й процентиль набора данных делит нижние k % набора данных из верхнего (100- к )%. Таким образом, 90-й процентиль делит нижние 90% от верхних 10%, то есть примерно 90% ниже и около 10% выше.

Используя StatCrunch, мы получаем следующий результат:

Следовательно, 90-й процентиль для показателей IQ составляет около 119.

Пример 10

Фото: A Syed

Предположим, что объем краски в 1-галлонных банках с краской производства Acme Paint Company приблизительно нормально распределен со средним значением 1,04 галлона и стандартным отклонением 0,023 галлона.

Какой объем, по словам компании Acme Paint Company, превышает 95% их банок?

[ раскрыть ответ ]

Это значение всего на 5% меньше указанного. Используя StatCrunch, мы получили следующий результат:

На основании этого расчета компания Acme Paint Company может сказать, что 95% ее банок содержат не менее 1,002 галлона краски.

Пример 11

Снова обратимся к весу годовалых мальчиков. (Вес годовалых мальчиков распределен примерно нормально, в среднем 22,8 фунта и стандартное отклонение около 2,15.)

Какой вес должен быть у годовалого мальчика, чтобы все, кроме 5% годовалых мальчиков, весили меньше, чем он?

[ раскрыть ответ ]

Снова используя StatCrunch, мы находим значение с площадью 0,95 слева:

Таким образом, годовалый мальчик должен весить около 26,3 фунтов. для всех, кроме 5% всех годовалых мальчиков, вес меньше, чем он.

Находка z

_α

Обозначение z _α («z-альфа») представляет собой Z-показатель с площадью α справа.

Концепция z _α широко используется на протяжении оставшейся части курса, поэтому важно один, чтобы быть удобным с. Приложения не будут сразу очевидны, но суть в том, что мы будем искать события маловероятные — а так имеют очень маленькую вероятность в «хвост».

Давайте попробуем несколько примеров.

Пример 12

а. Найти z _0,01

[ раскрыть ответ ]

С помощью StatCrunch получаем следующий результат:

Следовательно, z _0,01 = 2,33

б. Найти z _0,05

[ выявить ответ ]

Используя StatCrunch, мы получаем следующий результат:

Следовательно, z _0,05 = 1,64 (или 1,645)

c.