Высокая вариабельность при ктг что это: КТГ плода при беременности в СПб

Про ктг – кардиотокограмму. акцелерации при ктг норма

Пожаловаться

16 января 2010 21:30

Выложила 3 статьи разных авторов. Извините, если информация внутри каждой из них повторяется.

В настоящее время кардиотокография является, наряду с УЗИ, ведущим методом оценки состояния плода. Различают непрямую (наружную) и прямую (внутреннюю) КТГ. Во время беременности используется только непрямая КТГ. Современная кардитокограмма представляет собой две кривые, совмещенные по времени – одна из них отражает частоту сердечных сокращений плода, другая – маточную активность. Кроме того, современные фетальные мониторы снабжены приспособлением для графической регистрации движений плода.

Получение информации о сердечной деятельности плода осуществляется при помощи специального ультразвукового датчика, принцип работы которого основан на эффекте Доплера. 

Большинство авторов считают, что надежная информация о состоянии плода при использовании этого метода может быть получена только в III триместре беременности, с 32-34 недель.

Именно к этому времени достигает зрелости миокардиальный рефлекс и все другие проявления жизнедеятельности плода, оказывающие влияние на характер его сердечной деятельности, в частности, становление цикла активности и покоя плода. 

Ведущим при оценке состояния плода при использовании КТГ является активный период, поскольку изменения сердечной деятельности в период покоя аналогичны тем, которые наблюдаются при нарушении его состояния. Поэтому запись необходимо продолжать не менее 40 минут, т.к. фаза покоя плода в среднем составляет 15-30, реже до 40 минут.

При анализе кардиотокограмм последовательно анализируют величину базальной частоты сердечных сокращений, амплитуду мгновенных осцилляций, амплитуду медленных акцелераций, наличие и выраженность децелераций, двигательную активность плода.

Базальный ритм

Под базальным ритмом понимают среднюю частоту сердечных сокращений плода, сохраняющуюся неизменной за период, равный 10 мин и более. При этом акцелерации и децелерации не учитываются. При физиологическом состоянии плода частота сердечных сокращений подвержена постоянным небольшим изменениям, что обусловлено реактивностью автономной системы сердца плода.

Вариабельность сердечного ритма 

О вариабельности сердечного ритма судят по наличию мгновенных осцилляций. Они представляют собой отклонения ЧСС от среднего базального уровня. Подсчет осцилляций производится на участках, где нет медленных акцелераций. Подсчет количества осцилляций при визуальной оценке КТГ практически невозможен. Поэтому при анализе КТГ обычно ограничиваются подсчетом амплитуды мгновенных осцилляций. Различают низкие осцилляции (менее 3 сердечных сокращений в минуту), средние (3-6 в мин.) и высокие осцилляции (более 6 сердечных сокращений в минуту). Наличие высоких осцилляций свидетельствует о хорошем состоянии плода, низких – о нарушении его состояния.

Оссиляции

Особое внимание при анализе КТГ обращают на наличие медленных осцилляций. Подсчитывают их количество, амплитуду и продолжительность.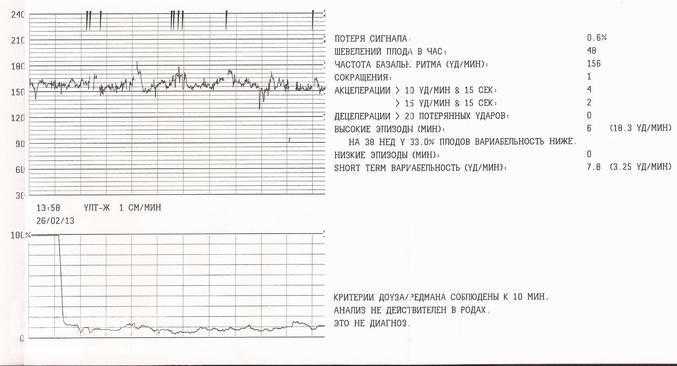

В зависимости от амплитуды медленных акцелераций различают следующие варианты КТГ: немой, или монотонный тип характеризуется низкой амплитудой осцилляций (0-5 уд/мин), слегка ундулирующий или переходный (6-10 уд/мин), ундулирующий или волнообразный (11-25 уд/мин), сальтаторный или скачущий (более 25 уд/мин). Наличие двух первых вариантов ритма обычно свидетельствует о нарушении состояния плода, ундулирующего о хорошем состоянии плода, сальтаторного – об обвитии пуповиной.

Акселерация

Акцелерацией называется увеличение ЧСС плода на 15 и более уд/мин, и продолжительностью более 15 секунд по сравнению с базальным ритмом. Увеличения ЧСС плода, имеющие параметры ниже указанных, трактуются как медленные осцилляции и относятся к показателю вариабельности. По форме акцелерации могут быть разнообразными (вариабельными) или похожими друг на друга (униформными). Появление на КТГ вариабельных спорадических акцелераций является наиболее достоверным признаком удовлетворительного состояния плода и с высокой вероятностью свидетельствует об отсутствии тяжелого ацидоза и гипоксического состояния плода.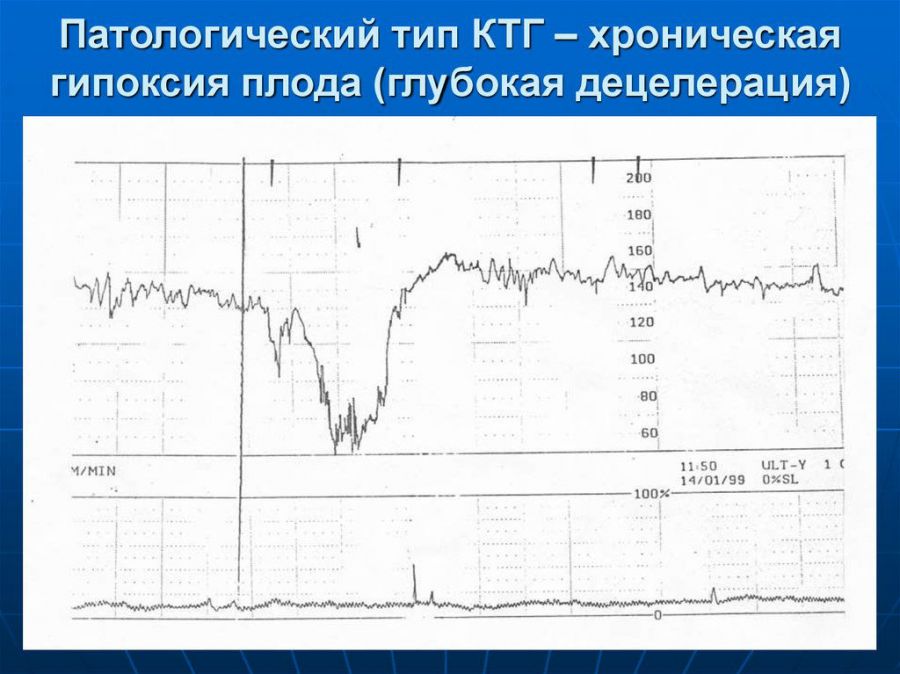

В то же время регистрация униформных периодических акцелераций, как бы повторяющих по форме маточные сокращения, свидетельствует об умеренной гипоксии плода, особенно в сочетании с тахикардией.

Децелерации

Помимо осцилляций и акцелераций, при расшифровке КТГ обращают внимание на децелерации (замедления ЧСС). Под децелерациями понимают эпизоды замедления ЧСС на 15 сердечных сокращений и более и продолжительностью 15 сек. и более. Децелерации обычно возникают в ответ на сокращения матки или движения плода.

Метод кардиотокографии обеспечивает одновременную регистрацию и запись на диаграммную ленту изменений во времени сердечного (кардио-) ритма плода и сократительной (токо-) активности матки.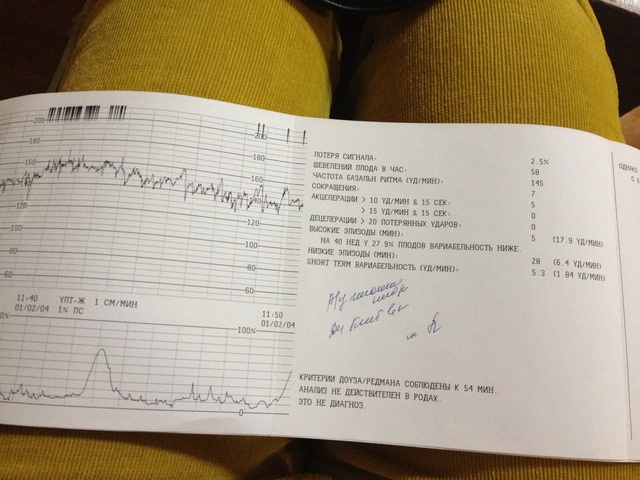

Один из самых первых кардиотокографов – аппаратов для записи КТГ, выпускавшихся американской компанией Хьюлет-Паккард в середине 70-х годов, был основан на акустической (фонокардиографической) регистрации тонов сердца плода. Однако вскоре стало ясно, что этот способ регистрации обладает низкой чувствительностью. В дальнейшем все КТГ-аппараты создавались на принципах допплеровской ультразвуковой локации движений клапанов сердца плода. Электронная система, встроенная в КТГ-аппарат, переводит последовательность допплеровских пиков сердечных сокращений в частоту сердцебиений (количество сердечных сокращений в мин.). Каждое значение длительности кардиоинтервала (периода между сокращениями) регистрируется на диаграммной ленте в виде точки. Поскольку лента движется очень медленно (1 см в мин), то точки эти сливаются и выстраиваются в достаточно неровную линию, показывающую, как в течение времени менялось мгновенное значение частоты сердечных сокращений (ЧСС) плода. Параллельно с записью ЧСС плода на втором канале прибора и при помощи другого датчика ведется регистрация изменений напряжения (тонуса) матки. Сопоставление изменений ЧСС плода с его двигательной активностью (определяемой либо матерью, либо самим аппаратом) и тонусом матки позволяет оценить состояние плода и сделать определенные прогнозы относительно развития данной беременности.

Метод КТГ довольно интенсивно развивался в течение 80-х – начале 90-х годов прошлого века и в настоящее время занял свое определенное место в ряду других методик оценки и диагностики состояния плода. КТГ используют не только для оценки состояния во время беременности, но и во время родов. Последнее направление чаще называют электронным мониторированием плода. В этом сообщении мы основное внимание уделим использованию КТГ во время беременности.

Прежде чем описывать диагностическое значение этого метода, остановимся на физиологии регуляции сердечного ритма плода. Сердце эмбриона человека начинает сокращаться на достаточно раннем этапе развития (в 4 недели) задолго до того, как возникает и начинает работать нервная система будущего человека. Ритм сокращений сердца задает группа клеток, находящихся в стенке правого предсердия и формирующих так называемый синусовый узел.

Электрический сигнал, возникающий в этих клетках, распространяется по специальной проводящей системе и вызывает скоординированное во времени сокращение всех отделов сердца, приводящее к изгнанию крови из желудочков сердца (систоле) и циркуляции крови по сосудистой системе плода.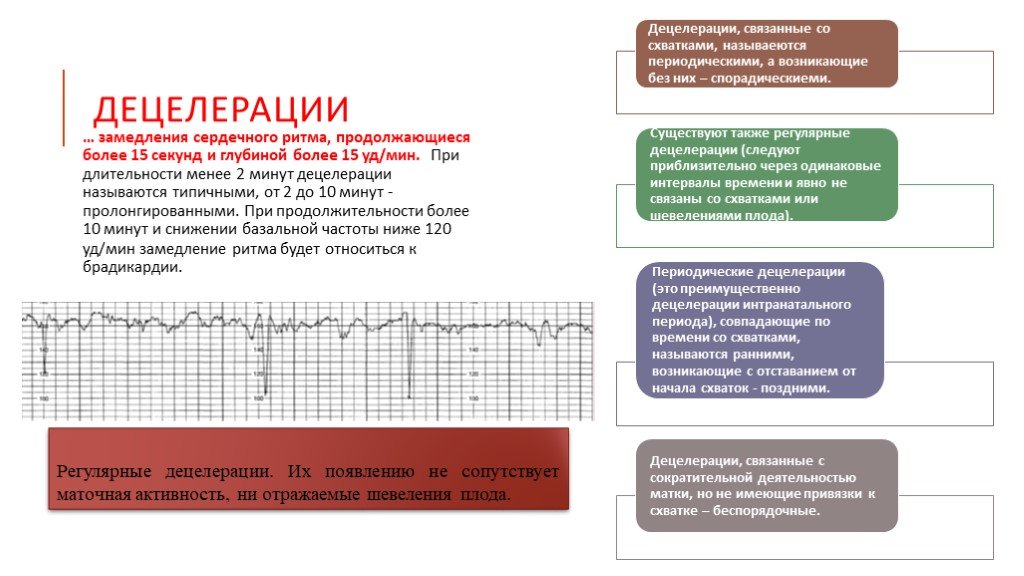

С 4 по 18 неделю внутриутробного развития сердце плода сокращается совершенно автономно и не находится под влиянием его нервной системы. Как известно, нервная система человека (как и всех животных) делится на две основных части – соматическую и вегетативную нервные системы. Соматическая (сома – тело) управляет нашими произвольными движениями. Вегетативная регулирует работу внутренних органов (сердца, легких, желудочно- кишечного тракта). Причем эта регуляция происходит непроизвольно без подключения наших умственных усилий. Ведь такие функции, как переваривание пищи, регуляция артериального давления, выделение желчи происходят как бы сами собой, без произвольных команд нашего сознания. Так же, как и остальные функции внутренних органов, частота сердцебиений находится под контролем нашей вегетативной системы. Если мы выполняем физическую работу – ЧСС увеличивается, если находимся в покое – уменьшается, что отражает запросы нашего организма в доставке кислорода к работающим органам. Увеличение ЧСС происходит под влиянием так называемого симпатического отдела вегетативной нервной системы.

Этот отдел реализует стрессорные реакции организма, готовит его к выполнению работы. Замедление ЧСС происходит под влиянием парасимпатического отдела. Этот отдел обеспечивает регуляцию деятельности органов в состоянии покоя, при переваривании пищи, во сне. Оба отдела находятся в состоянии динамического равновесия и осуществляют тонкую настройку и координацию работы всех органов органи зма для оптимального выполнения функций. Даже в состоянии покоя эти отделы работают и влияют на ритм сердцебиений. Попробуйте посчитать свой пульс в течение минуты. Окажется, что он, например, равен 62 удара в мин. Через три минуты повторите измерение и пульс уже окажется другим (например 72 удара в мин), а через 5 мин. измерение покажет 64 удара в мин. Эта нормальная вариабельность пульса, показывает то, что вегетативная нервная система организма работает и осуществляет небольшие изменения ЧСС в соответствии с температурой окружающей среды, ритмом дыхания и положением тела в пространстве, работой других внутренних органов. И наоборот, отсутствие вариабельности сердечного ритма свидетельствует о неполадках в организме. Так, у больных инфарктом миокарда или тяжелым гриппом вариабельность ЧСС значительно снижается. Все эти, с первого взгляда, заумные рассуждения непосредственным образом связаны с правильной интерпретацией результатов КТГ для оценки состояния плода.

Мы остановились на том, что до 18 недели сердце плода сокращается абсолютно автономно и не находится под влиянием вегетативной нервной системы. Но, начиная с 19 недели, тонкие веточки блуждающего нерва, относящегося к парасимпатической системе, прорастают к сердцу и начинают влиять на его работу. С этого срока ритм сердечных сокращений плода имеет несколько большую вариабельность. Двигательная активность плода в это время проявляется рефлекторными замедлениями сердечного ритма. Эти замедления называются децелерациями. Проникновение веточек симпатических нервов к сердцу плода происходит значительно позже – к 28-29 неделе беременности. С этого момента в ответ на двигательную активность плод начинает отвечать увеличением ЧСС – акцелерациями.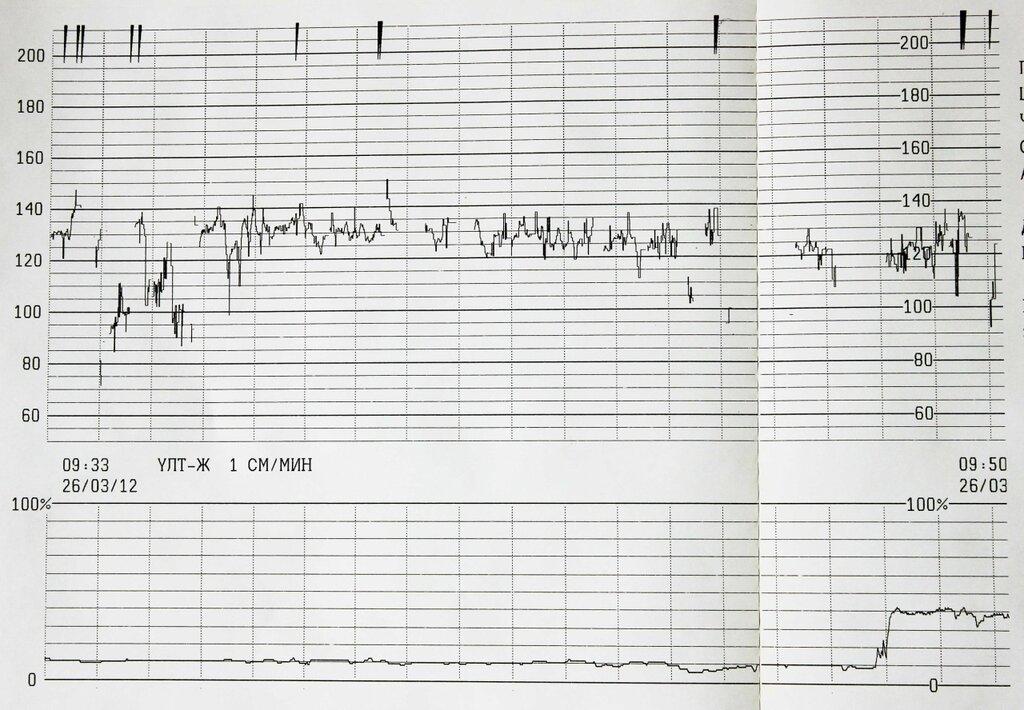 Это не значит, что до 28 недели мы не можем зарегистрировать периодических учащений сердцебиений плода, но они могут быть связаны с выделением биологически активных веществ в организме матери или с непосредственным влиянием условий внутриутробного существования на клетки синусового узла. До 32 недели происходит созревание механизмов нервной регуляции сердечной деятельности плода и уравновешивание влияния обоих отделов вегетативной нервной системы на регуляцию ЧСС плода. Поэтому оценка состояния плода по КТГ до 32 недели беременности не имеет существенного диагностического смысла. Во всяком случае, те диагностические критерии, которые выработаны для оценки КТГ доношенного плода в сроки до 32 недель, не работают.

Остановимся на этих критериях. При оценке КТГ, начиная с 32 недель, врач должен учитывать и оценивать следующие показатели:

1. Среднюю частоту сердцебиений (или базальный ритм).

В норме у плода он должен находиться в интервале 120-160 ударов в минуту.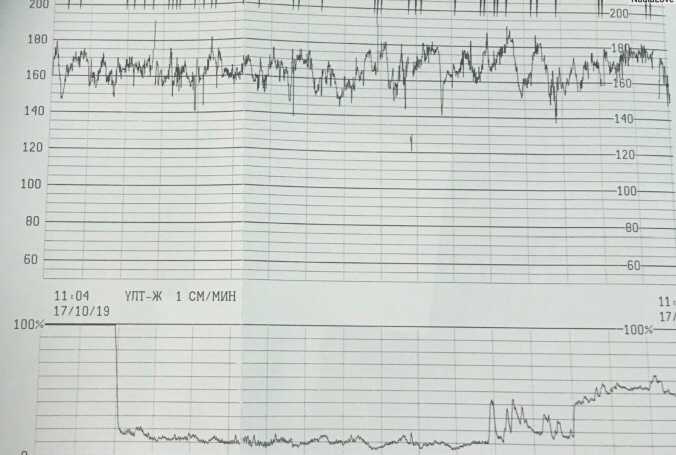
ЧСС выше 160 в мин называют тахикардией, ниже 120 в мин. – брадикардией.

2. Вариабельность сердечного ритма.

При этом выделяют так называемую краткосрочную вариабельность (насколько длительность текущего кардиоинтервала отличается от соседних) и долговременную (это небольшие изменения ЧСС в течение одной минуты). Оба эти вида связаны с регулирующим влиянием вегетативной нервной системы. Наличие вариабельности сердечного ритма является хорошим диагностическим признаком. Снижение вариабельности возможно как в норме (во время периодов сна ребенка), так и при хронической гипоксии. При гипоксии нарушаются тонкие регулирующие связи нервной системы и сердца. В результате сердце переходит на более автономный режим работы (менее связанный с деятельностью вегетативной нервной системы).

3. Наличие акцелераций.

Под акцелерацией понимают отклонение от базального ритма на 15 и более ударов в мин. в течение не менее 15 секунд. Наличие одной или нескольких акцелераций в течение 10 минутного отрезка записи является хорошим диагностическим признаком и свидетельствует о нормальной реактивности нервной системы плода. Хорошим признаком считается, когда после периода двигательной активности (этот период отмечает на записи сама женщина, нажимая кнопку, или специальная функция КТГ аппарата) регистрируется акцелерация.

4. Наличие децелераций.

Под децелерацией понимают периодическое замедление сердечного ритма плода на 15 и более уд. в минуту в течение 15 и более сек. Децелерация считается рефлекторной, когда она возникает после акцелерации или после эпизода двигательной активности. Такие децелерации не рассматриваются как проявление патологии. Несколько иначе обстоит дело со спонтанными глубокими децелерациями, которые могут возникнуть в покое или после маточных сокращений. Оценивают как патологию наличие глубоких децелераций с медленным восстановлением. Их возникновение может быть связано с прямым действием гипоксии на водитель ритма сердца плода.

5. Реакция на двигательную активность, стимуляцию плода или звук.

Для доношенного ребеночка нормальной реакцией на эти раздражители должна быть акцелерация.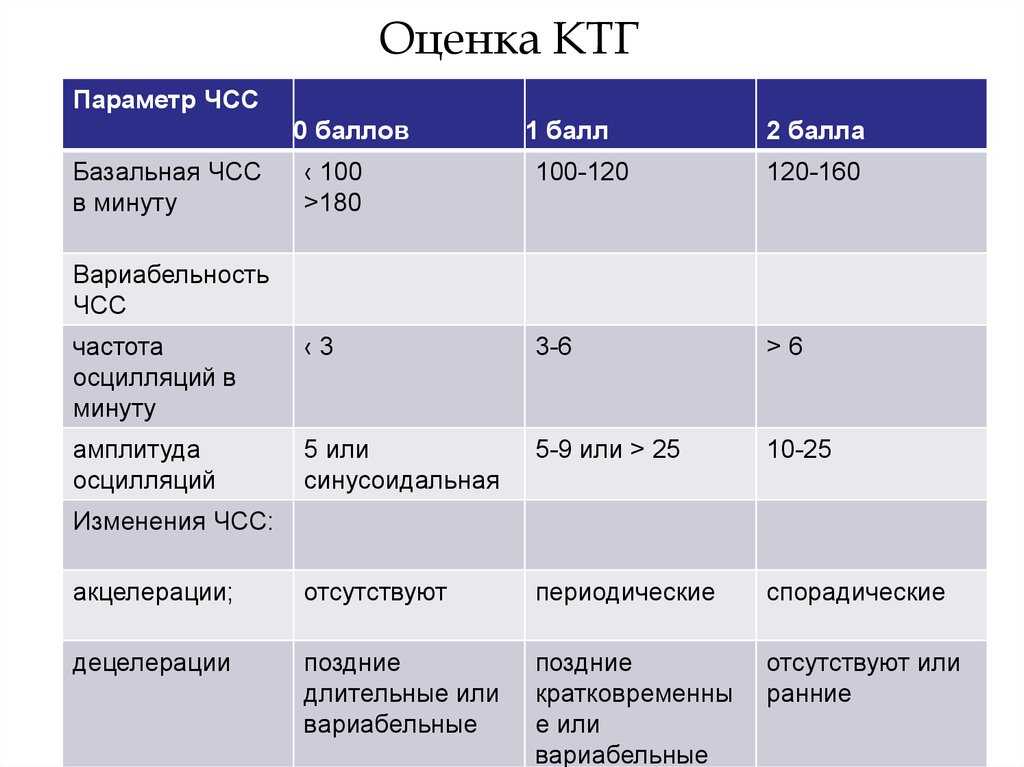

Очевидно, что оценивая КТГ по такому числу параметров (часть из которых являются количественными, другие – качественными), врач зачастую делает это весьма субъективно. Одна и та же запись сердечной деятельности плода может быть оценена различными экспертами как <нормальная> или признана <патологической>. Чтобы уменьшить вклад субъективного компонента, рядом исследователей были предложены шкалы количественной оценки КТГ. При этом каждый из параметров, в зависимости от соответствия его критериям нормы, оценивают от 0 до 2 баллов. Суммируя затем количество баллов, получают общую оценку кардиотокограммы. Наиболее известны шкалы Фишера (предложена в 1982 году) и Готье.

Сравнение исходов беременностей с результатами количественной балльной оценки КТГ до родов в большинстве случаев показало, что точность диагностики состояния плода этим методом все же недостаточно высока. Это неудивительно, поскольку КТГ – это попытка связать такой интегральный показатель, как частота сердечных сокращений плода (который может зависеть от большого числа неучтенных факторов – период сна плода, уровень глюкозы в крови матери и т.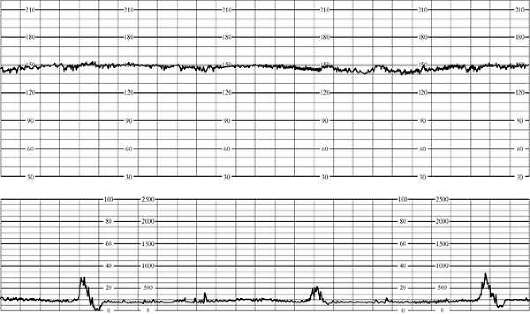 д.) с гипоксией плода (которая тоже имеет разнообразные проявления и может быть хронической и острой). Нередко ребенок находится в состоянии сна (ЧСС при этом характеризуется низкой вариабельностью), а КТГ его ошибочно может быть оценена как патологическая. Столкнувшись с этими обстоятельствами, еще в конце 80-х годов ряд исследователей сделали попытку компьютеризировать оценку КТГ. Наибольшие успехи в деле цифровой обработки сердечного ритма плода достигла группа акушеров и математиков из Оксфорда, возглавляемая профессорами Дэвисом и Рэдманом. Они проанализировали 8000 КТГ и сравнили их с состоянием новорожденных детей после родов. Это позволило точно знать, в каком случае имела место гипоксия плода, а в каком нет, что, в свою очередь, дало возможность связать количественные и качественные характеристики КТГ с уточненным состоянием плода. Результатом такой работы явилась разработка программного обеспечения для кардиотокографа фирмы Oxford, названного Team 8000. Такой аппарат регистрирует не только саму КТГ, но и считает ее основные параметры. Более того, процессор, встроенный в прибор, дает информацию, на какой минуте КТГ соответствует критерию Дэвиса-Рэдмана и может считаться нормальной для данного срока беременности. Несмотря на то, что результаты такой диагностики гипоксии плода стали значительно лучше, в конце отчета прибор делает отметку “Это не диагноз”. Это значит, что только врач при рассмотрении результатов всех клинических и инструментальных методов имеет право поставить клинический диагноз состояния плода.

Существенный прогресс ультразвуковых допплеровских методов измерения скорости кровотока в основных сосудах плода в норме и патологии поставил вопрос об оценке чувствительности и диагностической ценности этих методов по сравнению с КТГ. Большое количество исследований, проведенных на наиболее тяжелом контингенте беременных – женщинах с тяжелым гестозом и синдромом задержки развития плода показали, что при развитии патологии плода первыми меняются показатели скорости кровотока в артерии пуповины, центральной мозговой артерии. При дальнейшем прогрессировании патологии наблюдается уменьшение вариабельности сердечного ритма плода по КТГ, появление характерных децелераций и изменение допплеровских показателей в аорте и крупных венах плода.

Таким образом, КТГ является информативным и ценным методом диагностики состояния плода, но только в том случае, если применяется в комплексе с другими ультразвуковыми методами (фетометрией и допплерометрией).

Автор: Павел Борисович Цывьян, руководитель Центра подготовки к партнерским родам “Партнер”

КТГ (кардиотокография) представляет собой метод функциональной оценки состояния плода во время беременности и в родах на основании регистрации частоты его сердцебиений и их изменений в зависимости от сокращений матки, действия внешних раздражителей или активности самого плода.

КТГ в настоящее время является неотъемлемой частью комплексной оценки состояния плода наряду с ультразвуковым исследованием и допплерометрией. Такое наблюдение за сердечной деятельностью плода значительно расширяет возможности диагностики как во время беременности, так и в родах, и позволяет эффективно решать вопросы рациональной тактики их ведения.

Как проходит КТГ?

Сердечную деятельность плода регистрируют специальным ультразвуковым датчиком с частотой 1.5 – 2.0 Мгц, работа которого основана на эффекте Допплера. Этот датчик укрепляют на передней брюшной стенке беременной женщины в области наилучшей слышимости сердечных тонов плода, которую предварительно определяют с помощью обычного акушерского стетоскопа. Датчик генерирует ультразвуковой сигнал, который отражается от сердца плода и вновь воспринимается датчиком. Электронная система кардиомонитора преобразует зарегистрированные изменения интервалов между отдельными ударами сердца плода в мгновенную частоту его сердечных сокращений, рассчитывая количество ударов в минуту на момент исследования.

Изменения частоты сердечных сокращений отображается прибором в виде светового, звукового, цифрового сигналов и графического изображения в виде графика на бумажной ленте.

При выполнении КТГ одновременно с записью сердечной деятельности плода регистрируют сократительную активность матки специальным датчиком, который фиксируют на передней брюшной стенке беременной женщины в области дна матки.

В современных приборах для КТГ предусмотрен специальный пульт, с помощью которого беременная может самостоятельно фиксировать движения плода.

Сокращения матки и движения плода отображаются прибором в процессе исследования в нижней части бумажной ленты в виде кривой линии.

При расшифровке записи КТГ и оценке взаимосвязи полученных данных с состоянием плода следует исходить из того, что полученная запись отражает, прежде всего, реактивность нервной системы плода и состояние его защитно-приспособительных реакций на момент исследования.

Изменения сердечной деятельности плода только косвенно свидетельствуют о характере патологических процессов, происходящих в организме плода.

Нельзя отождествлять результаты, полученные при анализе записи КТГ, только с наличием той или иной степени выраженности кислородной недостаточности (гипоксии) у плода.

Вот всего лишь несколько примеров из множества возможных, подтверждающих эту мысль:

Гипоксия плода чаще всего обусловлена снижением доставки кислорода в маточно-плацентарный кровоток и нарушением функции плаценты.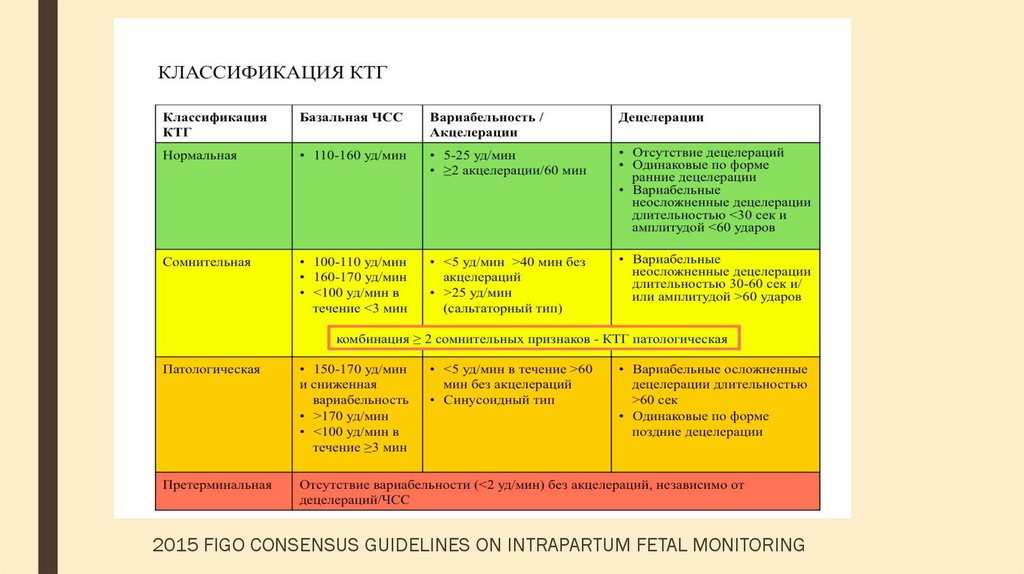 При этом ответная реакция сердечно-сосудистой системы плода возникает, соответственно, из-за наличия и степени выраженности снижения насыщения крови плода кислородом. Явное нарушение состояние плода при этом найдет свое соответствующее отражение в записи КТГ.

В ряде случаев возможно относительно кратковременное нарушение кровотока в сосудах пуповины, например, вследствие их прижатия головкой плода. Это явление также будет отражаться на характере записи КТГ, как бы придавая ей патологический характер, хотя, на самом деле, плод и не страдает. При этом создается ложная иллюзия о нарушении состояния плода.

В качестве защитной реакции у плода может снижаться потребляемость кислорода тканями и повышается устойчивость к гипоксии. Запись КТГ при этом будет нормальной, несмотря на то, что плод испытывает гипоксию. Просто при этом ситуация пока еще остается компенсированной.

При различных патологических состояниях возможно снижение способности тканей к восприятию кислорода при нормальном его содержании в крови, что может не вызвать соответствующей реакции сердечно-сосудистой системы плода, несмотря на то, что ткани плода испытывают недостаток кислорода и плод страдает. Т.е. при такой ситуации запись КТГ будет нормальной, несмотря на нарушение состояния плода.

Таким образом, КТГ является всего лишь дополнительным инструментальным методом диагностики, а информация, получаемая в результате исследования, отражает только небольшую часть сложных изменений, происходящих в системе мать-плацента-плод. Полученную при исследовании с помощью КТГ информацию необходимо сопоставлять с клиническими данными и результатами других исследований, так как две похожие записи с почти одинаковыми диагностическими характеристиками могут иметь совершенно различное диагностическое значение для разных плодов.

Условия для проведения КТГ

Для получения достоверной информации о состоянии плода на основании данных КТГ следует соблюдать ряд условий:

Использовать КТГ можно не раньше, чем с 32 недель беременности. К этому времени формируется взаимосвязь между сердечной деятельностью и двигательной активностью плода, что отражает функциональные возможности нескольких его систем (центральной нервной, мышечной и сердечно-сосудистой).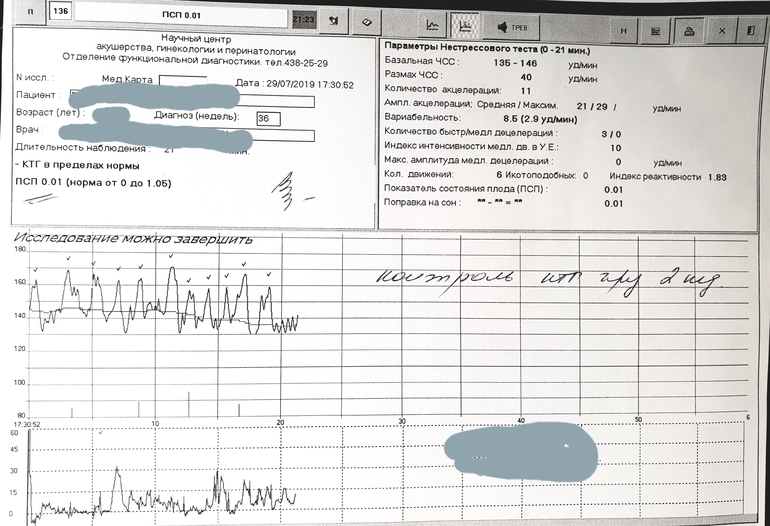 К 32-й неделе беременности происходит также становление цикла активность-покой плода. При этом средняя продолжительность активного состояния составляет 50-60 мин, а спокойного – 20-30 мин. Более раннее использование КТГ не обеспечивает достоверности диагностики, так как сопровождается получением большого количества ложных результатов.

Первостепенное значение в оценке состояния плода имеет период его активности. Важно, чтобы за время выполнения КТГ была зафиксирована хотя бы часть периода активности плода, сопровождаемого его движениями. С учетом спокойного состояния плода необходимая общая продолжительность записи должна составлять 40-60 мин, что сводит к минимуму возможную ошибку в оценке функционального состояния плода.

Запись осуществляют в положении беременной на спине, на левом боку или сидя в удобном положении.

С одной стороны, существует мнение о недостаточной информативности КТГ в диагностике нарушений состояния плода, о чем свидетельствует немалое количество ложноположительных результатов в группе с патологическими изменениями на кардиотокограмме.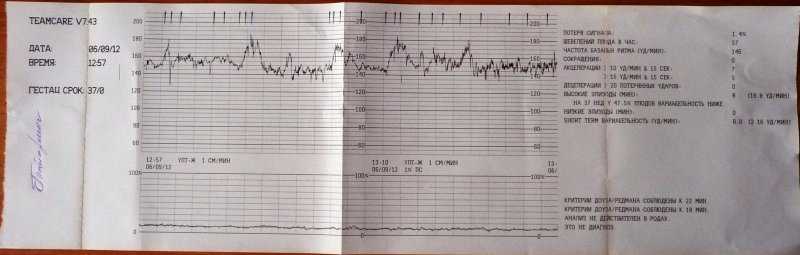 По другим данным точность прогноза удовлетворительного состояния новорожденных совпала с результатами КТГ более чем в 90% случаев, что указывает на высокую способность метода в подтверждении нормального состояния плода. Однако, на самом деле информативность метода во многом зависит от способа интерпретации полученных при исследовании данных.

При расшифровке записи КТГ определяют ряд показателей, имеющих нормальные и патологические признаки, которые позволяют оценить состояние реактивности сердечно-сосудистой системы плода.

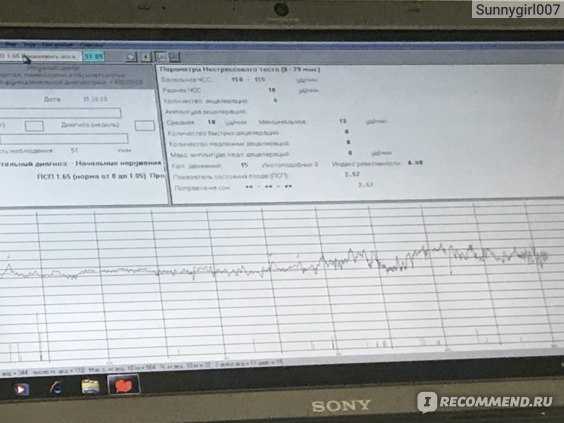
В целом ряде случаев используют методы компьютерной оценки записи КТГ. Так, в частности, при интерпретации данных КТГ используют расчет показателя состояния плода – ПСП. При этом значения ПСП 1 и менее могут свидетельствовать о нормальном состоянии плода. Значения ПСП более 1 и до 2 могут указывать на возможные начальные проявления нарушения состояния плода. Значения ПСП более 2 и до 3 могут быть обусловлены вероятностью выраженных нарушений состояния плода. Величина ПСП более 3 указывает на возможное критическое состояние плода. Широко применяются также различные шкалы оценки показателей КТГ в баллах.

Среди них наиболее распространены шкалы, предложенные W.Fischer и др.(1976), Е.С.Готье и др. (1982), а также их различные модификации. При этом оценка 8-10 баллов соответствует нормальной КТГ; 5-7 баллов является подозрительной и может указывать на начальные проявления нарушения состояния плода; 4 балла и менее могут свидетельствовать о значительных нарушениях в состоянии плода.

Однако к этим показателям следует относиться весьма осторожно и дифференцированно. Следует понимать, что заключение по расшифровке записи КТГ не является диагнозом, а только представляет некоторую дополнительную информацию наряду с другими методами исследования. Результаты однократного исследования дают только косвенное представление о состоянии плода с момента исследования не более, чем на сутки. В силу различных обстоятельств характер реактивности сердечно-сосудистой системы плода может изменяться и за более короткое время. Степень выраженности нарушений реактивности сердечно-сосудистой системы плода не всегда может совпадать с тяжестью нарушения его состояния. Полученные результаты необходимо рассматривать только во взаимосвязи с клинической картиной, характером течения беременности и данными других методов исследования, включая УЗИ и допплерометрию.

Тем не менее, метод КТГ не имеет противопоказаний и является абсолютно безвредным. Исходя из этого, использование КТГ во время беременности позволяет проводить мониторирование состояния плода на протяжении длительного времени, а при необходимости это можно делать и ежедневно, что значительно повышает диагностическую ценность метода, особенно в сочетании с данными других методов диагностики. КТГ успешно используется и во время родов, что позволяет контролировать состояние плода в динамике родов и оценивать сокращения матки. Данные КТГ облегчают оценку эффективности проводимого лечения в родах и, нередко, полученные результаты исследования являются поводом для изменения тактики ведения родов.

В идеальном варианте роды у каждой женщины следует вести под контролем КТГ. Особое внимание следует уделять преждевременным и запоздалым родам, возбуждению и стимуляции родовой деятельности, родам при тазовом предлежании плода, а также родам при фетоплацентарной недостаточности и гипоксии плода. Результаты КТГ в родах также расценивают строго индивидуально и только в комплексе с клиническими данными, а также с результатами других исследований, проведенных накануне или во время родов.

Автор: Макаров Игорь Олегович, доктор медицинских наук, профессор, врач высшей квалификационной категории, медицинский центр “Арт-Мед”

Рубрика Обследования, анализы

7092311

Следующая статья

Как облегчить изжогу или даже избавится от неё?

Другие статьи на эту тему

• Показатели давления и ЧСС
• Интерпретация результатов анализа
• Синусовая брадикардия у ребенка
• Изменение маточно плацентарного кровотока
• Синусовая брадикардия

Актуальные посты

с какого возраста можно давать ребенку сок
дексаметазон для чего назначают

Узнавай и участвуй

Клубы на Бэби. ру — это кладезь полезной информации

ТОП-25 Новогодних подарков для детей всех возрастовПомощь государства детям с диабетомТоп-10 девайсов для кормящей мамыКакую детскую одежду вы покупаете?Оцените состояние иммунитета вашего ребенкаОнлайн приёмная психолога — для мам часто болеющих детейПочему ребенок часто болеет?

КТГ плода — цена в Москве

Классическое выслушивание сердцебиения плода обеспечивает недостаточно информации о его состоянии. Поэтому для пренатальной оценки сердечной деятельности используется кардиотокография (КТГ). По информативности и простоте этот метод превосходит не только аускультацию, но и такие способы диагностики, как электрокардиография и фонокардиография.

Что такое кардиотокография

КТГ — технология оценки функционального состояния плода, основанный на записи изменений коронарного ритма во время его движения или сокращения матки. Основная цель — выявление хронической гипоксии. Регистрация данных производится с помощью ультразвукового и тензометрического датчика, поэтому процедура не представляет никакой опасности для будущего ребенка. Ионизирующее излучение и другие физические факторы, способные нанести ему вред, не применяются.

Кардиотокографию назначают на сроке беременности более 32 недель. К этому времени у плода формируется миокардиальный рефлекс, а также устанавливаются периоды активности и покоя. Исследование стараются проводить, когда ребенок подвижен. Записи, сделанные во время сна, напоминают таковые при определенных нарушениях и затрудняют интерпретацию.

Обследование может осуществляться и во время родов. При этом врачи используют прямой метод. К предлежащей части плода подводится спиралевидный электрод, а тонус матки регистрируется с помощью введенного в нее катетера. Своевременная КТГ позволяет выявить факт гипоксии и определить ее тяжесть. Это необходимо для сохранения жизни ребенка и матери.

Цены на КТГ плода

КТГ плода

1000 ₽

Показания и противопоказания

КТГ назначается с профилактической целью. Она входит в состав диагностического комплекса, который позволяет исключить аномалии развития плода. Показанием к процедуре врачи считают:

• болезни женщины во время беременности: эклампсия, тяжелые инфекции, отравление;
• ослабление двигательной активности плода;
• неясные абдоминальные боли;
• травмы и удары в область живота в анамнезе;
• патологические явления во время предыдущих беременностей и родов;
• любые другие состояния, ставящие под угрозу жизнь и здоровье будущего ребенка.

Противопоказания к кардиотокографии отсутствуют, так как во время процедуры на женщину не влияют факторы, способные навредить ей или плоду. Не рекомендуется осуществлять манипуляцию после приема кофе, энергетических напитков, курения. В таких случаях результаты будут не совсем корректными.

Как проходит КТГ плода

Обследование проводится амбулаторно, в кабинете функциональной диагностики акушерского центра. Женщину укладывают на спину с легким наклоном на левый бок. Головной конец кушетки приподнимают. Также возможно регистрация КТГ в положении сидя.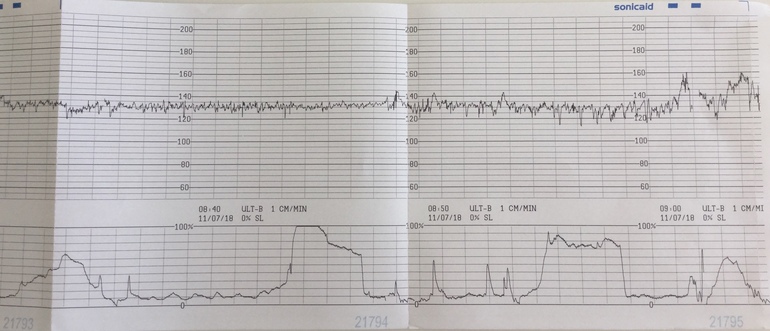 Врач с помощью стетоскопа определяет, где лучше всего выслушивается сердцебиение плода. Сюда накладывается ультразвуковой датчик. Тензометрическое устройство фиксируют на передней брюшной стенке.

Когда ведется запись, лучше сохранять неподвижность. Допускаются незначительные изменения положения тела, которые никак не влияют на результат процедуры. Информация о состоянии матки и сердечной деятельности плода записывается на бумажную ленту в виде двух кривых. Позднее их расшифровкой занимается врач. Продолжительность исследования варьирует от 15–20 минут до 1 часа. Она зависит от уровня активности ребенка.

Результаты

Оценка КТГ может производиться с помощью автоматизированных средств или вручную. Во втором случае точность результатов в значительной степени зависит от опыта и профессиональных навыков специалиста по функциональной диагностике. При описании токограмм учитывается 5 основных параметров.

1. Базальный ритм. Средняя ЧСС, которая сохраняется на протяжении минимум 10 минут. В норме составляет 120–160 ударов в минуту.
2. Вариабельность. Незначительные изменения сердечного цикла плода, спровоцированные высокой реактивностью его нервной системы. Показатель не должен превышать 10–25 уд/минуту.
3. Осцилляция. Числовое выражение вариабельности. Подсчитывается по амплитуде и частоте эпизодов, возникших в течение 10 минут. По времени занимает 2–10 секунд.
4. Акцелерация. Эпизод увеличения сердечного ритма на 15 и более ударов в минуту, по времени превышающий 10 секунд. В норме акцелерации возникают не менее 2 раз за десятиминутный период.
5. Децелерация. Замедление ритма на 15 и более ударов/минуту, которое регистрируется дольше 10 секунд. На нормальной кардиотокограмме подобные явления отсутствуют.

Результаты КТГ выражаются в баллах. Используются различные модификации шкалы Фишера, разработанной в 1976 году. Согласно ей, оценка в 8–10 баллов соответствует здоровому ребенку, 5–7 баллов — свидетельство начинающихся нарушений. 4 единицы и менее выставляется при существенной, часто жизнеугрожающей патологии.

Точное совпадение данных кардиотокографии с информацией, полученной в ходе других обследований, достигает 74 %. В остальных случаях расхождение составляет 1–2 балла, что не является критичным. Серьезные различия встречаются не чаще, чем в 3,5 % случаев. Большинство подобных ситуаций связано с недостаточно точной ручной расшифровкой результатов, проведенной молодыми врачами.

КТГ — информативный метод оценки состояния плода. Он может использоваться как самостоятельно, так и в составе комплексных схем диагностики. Сравнительно низкая цена делает процедуру доступной для большинства женщин. Манипуляция совершенно безболезненна и безопасна. Жители Московского региона могут пройти кардиотокографию в акушерском центре «Дар жизни».

Расчет диапазона, IQR, дисперсии, стандартного отклонения

Изменчивость описывает, насколько далеко точки данных расположены друг от друга и от центра распределения. Наряду с мерами центральной тенденции меры изменчивости дают вам описательную статистику, которая обобщает ваши данные.

Изменчивость также называется разбросом, разбросом или дисперсией. Чаще всего измеряется следующим образом:

• Диапазон: разница между самым высоким и самым низким значением
• Межквартильный диапазон: диапазон средней половины распределения
• Стандартное отклонение: среднее расстояние от среднего
• Дисперсия: среднее квадратов расстояний от среднего

Содержание

1. Почему важна изменчивость?
2. Диапазон
3. Межквартильный диапазон
4. Стандартное отклонение
5. Дисперсия
6. Как лучше всего измерять вариабельность?
7. Часто задаваемые вопросы об изменчивости

Почему важна изменчивость?

В то время как центральная тенденция, или среднее, говорит вам, где находится большинство ваших точек, изменчивость суммирует, насколько далеко они друг от друга. Это важно, потому что степень изменчивости определяет, насколько хорошо вы можете обобщить результаты выборки на вашу совокупность.

Низкая изменчивость идеальна, потому что это означает, что вы можете лучше прогнозировать информацию о генеральной совокупности на основе выборочных данных. Высокая изменчивость означает, что значения менее постоянны, поэтому делать прогнозы сложнее.

Наборы данных могут иметь одну и ту же центральную тенденцию, но разные уровни изменчивости или наоборот. Если вы знаете только центральную тенденцию или изменчивость, вы ничего не можете сказать о другом аспекте. Оба они вместе дают вам полную картину ваших данных.

Пример: изменчивость в нормальном распределении. Вы исследуете количество времени, ежедневно проводимого разными группами людей за телефоном.

Используя простые случайные выборки, вы собираете данные из 3 групп:

• Образец A: старшеклассники,
• Образец B: студенты колледжа,
• Образец C: взрослые штатные сотрудники.

Все три ваших образца используют телефон в среднем одинаково: 195 минут или 3 часа 15 минут. Это значение по оси x, где находятся пики кривых.

Хотя данные имеют нормальное распределение, каждая выборка имеет разный разброс. Образец А имеет наибольшую изменчивость, тогда как образец С имеет наименьшую изменчивость.

Диапазон

Диапазон показывает разброс ваших данных от самого низкого до самого высокого значения в распределении. Это самая простая мера изменчивости для расчета.

Чтобы найти диапазон, просто вычтите наименьшее значение из наибольшего значения в наборе данных.

Пример диапазона У вас есть 8 точек данных из образца A.

Данные (минуты)	72	110	134	190	238	287	305	324

Наибольшее значение ( H ) равно 324 , а наименьшее ( L ) равно 72 .

П = В – Л

Ч = 324 – 72 = 252

Диапазон ваших данных: 252 минуты .

Поскольку используются только 2 числа, диапазон зависит от выбросов и не дает никакой информации о распределении значений. Лучше всего использовать его в сочетании с другими мерами.

Что может сделать корректура для вашей статьи?

Редакторы Scribbr не только исправляют грамматические и орфографические ошибки, но и улучшают качество письма, следя за тем, чтобы в статье не было неясных выражений, избыточных слов и неудобных формулировок.

См. пример редактирования

Межквартильный диапазон

Межквартильный диапазон дает вам спред середины вашего распределения.

Для любого распределения, упорядоченного от низкого к высокому, межквартильный диапазон содержит половину значений. В то время как первый квартиль (Q1) содержит первые 25% значений, четвертый квартиль (Q4) содержит последние 25% значений.

Межквартильный диапазон равен третьему квартилю (Q3) минус первый квартиль (Q1). Это дает нам диапазон средней половины набора данных.

Пример межквартильного диапазона Чтобы найти межквартильный диапазон ваших 8 точек данных, вы сначала находите значения в Q1 и Q3.

Умножьте количество значений в наборе данных (8) на 0,25 для 25-го процентиля (Q1) и на 0,75 для 75-го процентиля (Q3).

Позиция Q1: 0,25 x 8 = 2

Позиция Q3: 0,75 x 8 = 6

Q1 — это значение во 2-й позиции, которое равно 110 . Q3 — это значение на 6-й позиции, равное 287 .

IQR = Q3 – Q1

ИКР = 287 – 110 = 177

Межквартильный диапазон ваших данных: 177 минут .

Как и диапазон, межквартильный диапазон использует при расчете только 2 значения. Но выбросы меньше влияют на IQR: два значения взяты из средней половины набора данных, поэтому вряд ли они будут крайними значениями.

IQR дает последовательную меру изменчивости как для асимметричных, так и для нормальных распределений.

Итог из пяти цифр

Каждое распределение может быть организовано с использованием пятизначной сводки :

• Наименьшее значение
• Q1: 25-й процентиль
• Q2: медиана
• Q3: 75-й процентиль
• Максимальное значение (Q4)

Эти сводки из пяти чисел можно легко визуализировать с помощью диаграмм с ячейками и усами.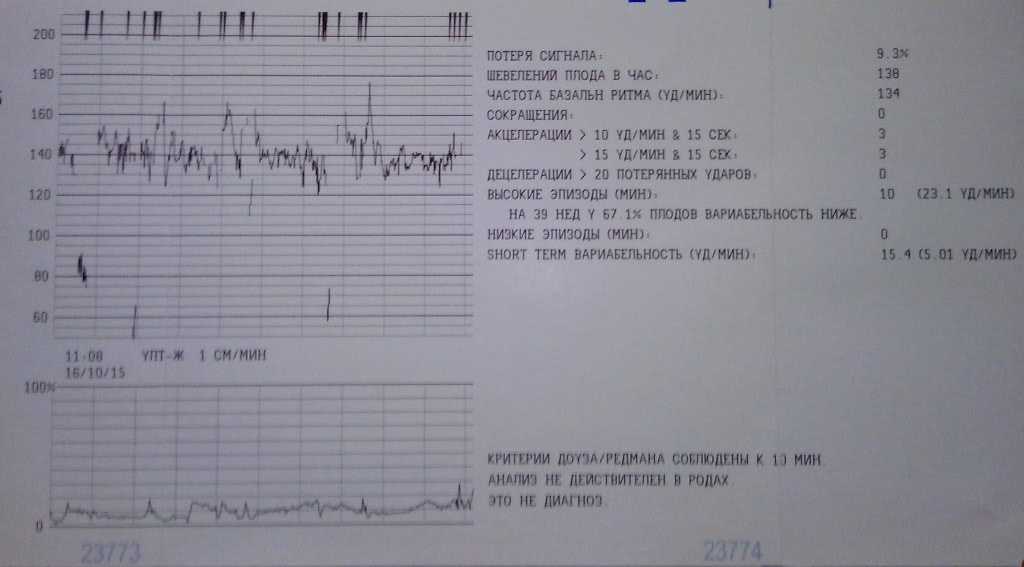

Пример графика прямоугольника и усов Для каждого из наших образцов горизонтальные линии в прямоугольнике показывают Q1, медиану и Q3, а усы в конце показывают самые высокие и самые низкие значения.

Стандартное отклонение

Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных.

Показывает, в среднем, насколько далеко каждая оценка от среднего. Чем больше стандартное отклонение, тем более изменчив набор данных.

Существует шесть шагов для нахождения стандартного отклонения вручную:

1. Перечислите все баллы и найдите их среднее значение.
2. Вычтите среднее из каждой оценки, чтобы получить отклонение от среднего.
3. Возведите в квадрат каждое из этих отклонений.
4. Сложите все квадраты отклонений.
5. Разделить сумму квадратов отклонений на n – 1 (для выборки) или N (для генеральной совокупности).
6. Найдите квадратный корень из найденного числа.

Пример стандартного отклонения

Шаг 1: Данные (минуты)	Шаг 2: отклонение от среднего	Шаги 3 + 4: Квадрат отклонения
72	72 – 207,5 = -135,5	18360.25
110	110 – 207,5 = -97,5	9506.25
134	134 – 207,5 = -73,5	5402.25
190	190 – 207,5 = -17,5	306,25
238	238 – 207,5 = 30,5	930,25
287	287 – 207,5 = 79,5	6320.25
305	305 – 207,5 = 97,5	9506.25
324	324 – 207,5 = 116,5	13572.25
Среднее = 207,5	Сумма = 0	Сумма квадратов = 63904

Пример стандартного отклоненияПоскольку вы имеете дело с образцом, вы используете п – 1.

n – 1 = 7

63904 / 7 = 9129,14

Пример стандартного отклонения

с = √9129,14 = 95,54

Стандартное отклонение ваших данных составляет 95,54 . Это означает, что в среднем каждая оценка отклоняется от среднего значения на 95,54 балла.

Формула стандартного отклонения для совокупностей

Если у вас есть данные по всей совокупности, используйте формулу стандартного отклонения совокупности:

Формула	Пояснение
	= стандартное отклонение совокупности = сумма… = каждое значение = средняя численность населения = количество значений в совокупности

Формула стандартного отклонения для проб

Если у вас есть данные из выборки, используйте формулу стандартного отклонения выборки:

Формула	Пояснение
	= стандартное отклонение выборки = сумма… = каждое значение  = выборочное среднее = количество значений в выборке

Зачем использовать

n – 1 для стандартного отклонения выборки?

Выборки используются для статистических выводов о населении, из которого они взяты.

Когда у вас есть данные о населении, вы можете получить точное значение стандартного отклонения населенности. Поскольку вы собираете данные от каждого члена совокупности, стандартное отклонение отражает точную величину изменчивости в вашем распределении, совокупности.

Но когда вы используете данные выборки, стандартное отклонение вашей выборки всегда используется в качестве оценки стандартного отклонения генеральной совокупности. Использование n в этой формуле может дать вам необъективную оценку, которая последовательно занижает изменчивость.

При уменьшении выборки n до n – 1 стандартное отклонение искусственно увеличивается, что дает вам консервативную оценку изменчивости.

Хотя это и не беспристрастная оценка, это менее предвзятая оценка стандартного отклонения: лучше переоценить, чем недооценить изменчивость выборок.

Разница между предвзятыми и консервативными оценками стандартного отклонения становится намного меньше, когда у вас большой размер выборки.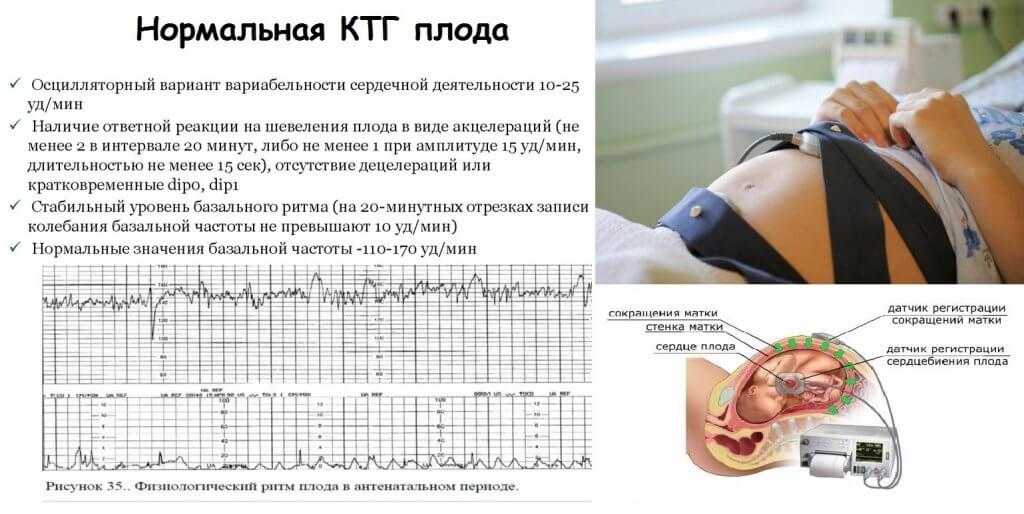

Дисперсия

Дисперсия — это среднее квадратов отклонений от среднего. Отклонение от среднего — это то, насколько далеко результат находится от среднего.

Дисперсия — это квадрат стандартного отклонения. Это означает, что единицы дисперсии намного больше, чем единицы типичного значения набора данных.

Хотя интуитивно интерпретировать число дисперсии сложнее, важно вычислить дисперсию для сравнения различных наборов данных в статистических тестах, таких как ANOVA.

Дисперсия отражает степень разброса в наборе данных. Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению.

Пример дисперсии Чтобы получить дисперсию, возведите стандартное отклонение в квадрат.

с = 95,5

с ² = 95,5 х 95,5 = 9129,14

Дисперсия ваших данных составляет 9129,14.

Чтобы найти дисперсию вручную, выполните все шаги для стандартного отклонения, кроме последнего шага.

Формула дисперсии для совокупностей

Формула	Пояснение
	= дисперсия населения = сумма… = каждое значение = средняя численность населения = количество значений в совокупности

Формула дисперсии для проб

Формула	Пояснение
	= выборочная дисперсия = сумма… = каждое значение = выборочное среднее = количество значений в выборке

Смещенные и несмещенные оценки дисперсии

Беспристрастная оценка в статистике — это оценка, которая не всегда дает вам ни высокие, ни низкие значения — она не имеет систематической погрешности.

Как и для стандартного отклонения, существуют разные формулы для генеральной совокупности и выборочной дисперсии.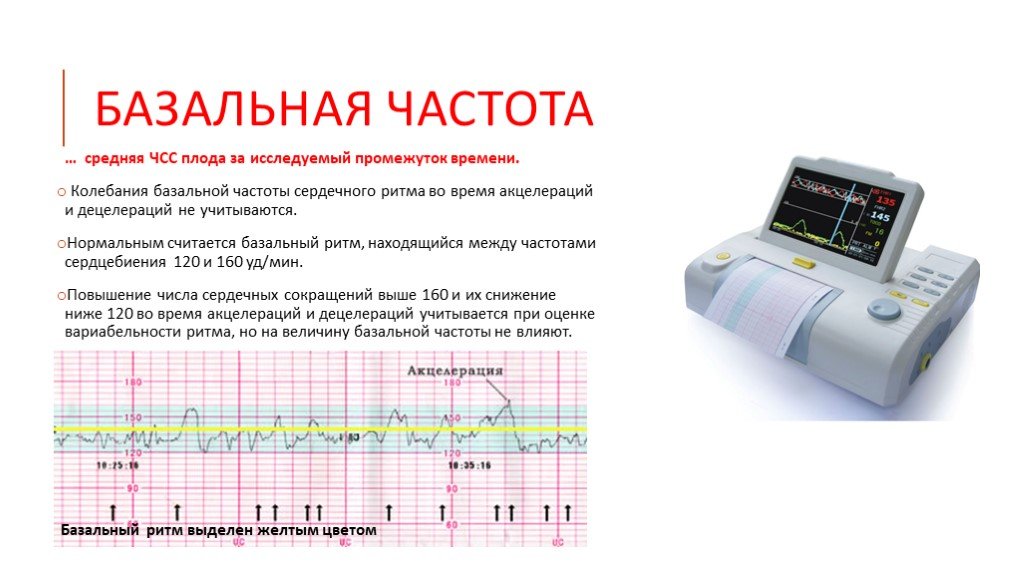 Но хотя не существует объективной оценки стандартного отклонения, она есть для выборочной дисперсии.

Если бы в формуле выборочной дисперсии использовалась выборка n , выборочная дисперсия была бы смещена в сторону меньших чисел, чем ожидалось. Уменьшение выборки n до n – 1 искусственно увеличивает дисперсию.

В этом случае смещение не только снижается, но и полностью устраняется. Формула выборочной дисперсии дает полностью объективные оценки дисперсии.

Так почему же стандартное отклонение выборки не является также объективной оценкой?

Это потому, что стандартное отклонение выборки получается из нахождения квадратного корня выборочной дисперсии. Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.

Что является наилучшей мерой изменчивости?

Наилучшая мера изменчивости зависит от вашего уровня измерения и распределения.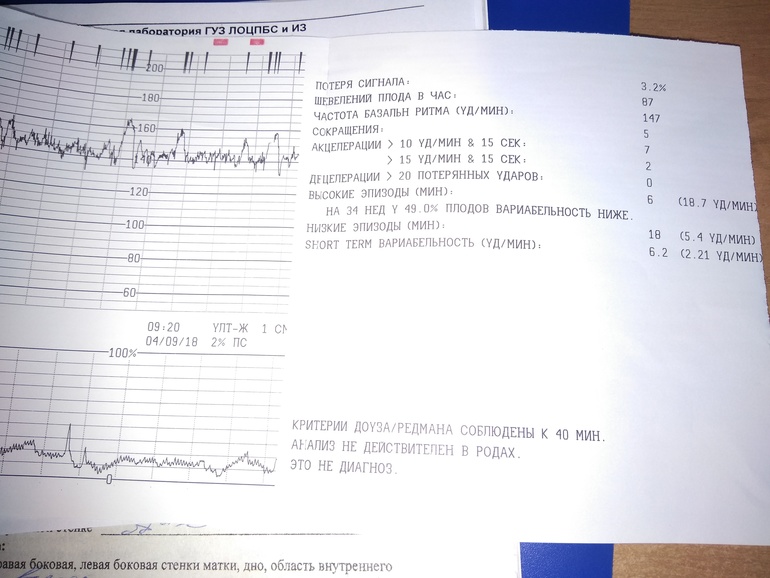

Уровень измерения

Для данных, измеренных на порядковом уровне, диапазон и межквартильный диапазон являются единственными подходящими показателями изменчивости.

Для более сложных уровней интервалов и отношений также применимы стандартное отклонение и дисперсия.

Распределение

Для нормальных распределений можно использовать все меры. Стандартное отклонение и дисперсия предпочтительнее, потому что они учитывают весь ваш набор данных, но это также означает, что на них легко влияют выбросы.

Для асимметричных распределений или наборов данных с выбросами наилучшим показателем является межквартильный диапазон. На него меньше всего влияют экстремальные значения, поскольку он фокусируется на разбросе в середине набора данных.

Часто задаваемые вопросы об изменчивости

Что такое изменчивость?

org/Answer»>

Изменчивость говорит вам, как далеко точки находятся друг от друга и от центра распределения или набора данных.

Изменчивость также называется распространением, разбросом или дисперсией.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Бхандари, П. (2022, 11 ноября). Изменчивость | Расчет диапазона, IQR, дисперсии, стандартного отклонения. Скриббр. Проверено 28 ноября 2022 г., с https://www.scribbr.com/statistics/variability/

Процитировать эту статью

Кинетическая теория газов: краткий обзор

Физика 252: Современная физика! предыдущий индекс следующий Физика 152: предыдущий индекс следующий

Майкл Фаулер

Рисунок Бернулли

Даниил Бернулли в 1738 году первым понял воздух давление с молекулярной точки зрения.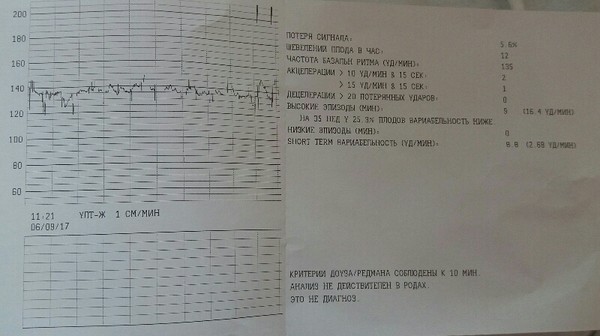 Он нарисовал вертикальную цилиндр, закрытый снизу, с поршнем вверху, поршень с грузом на нем, поршень и груз являются поддерживается давлением воздуха внутри цилиндра.

Он описал, что происходило внутри цилиндра следующим образом: « пусть полости содержат мельчайшие тельца, которые перемещаются туда-сюда с очень быстрое движение; так что эти корпускулы, когда они ударяются о поршень и поддерживают его своими повторяющимися ударами, образуют упругую жидкость, которая будет расширяться сам по себе, если вес будет удален или уменьшен… ”

Печально сообщать, что его проницательность, хотя по сути верная, не получил широкого признания. Большинство ученых считало, что молекулы газа оставались более или менее на месте, отталкивая друг друга издалека, держались как-то в эфире. Ньютон показал, что PV=константа следует, если отталкивание обратный квадрат. Фактически, в 1820-х годах англичанин Джон Герапат вывел взаимосвязь между давлением и молекулярной скоростью, приведенную ниже, и попытался издайте его Королевским обществом. Он был отклонен президентом, Гемфри Дэви, который указал, что приравнивание температуры к движению, как Герапат подразумевал, что будет абсолютный нуль температуры, идея, которую Дэви не хотел принимать. А также следует добавить, что никто не имел ни малейшего представления о том, насколько велики атомы и молекулы были, хотя Авогадро предположил, что равные объемы различные газы при одинаковых температуре и давлении содержат одинаковое количество молекулы — его знаменитая номер — ни он никто другой не знал, что это за число, только то, что оно было довольно большим.

Связь между молекулярной энергией и давлением

Нетрудно расширить картину Бернулли до количественного описание, связывающее давление газа с молекулярными скоростями. Как тепло Чтобы выполнить упражнение, давайте рассмотрим единственную идеально упругую частицу массы m, быстро подпрыгивающую вперед и назад со скоростью v внутри узкого цилиндра длиной L с поршнем на одном конце, так что все движение по той же линии. (Чтобы посмотреть фильм, нажмите вот!) Какое усилие на поршне?

Очевидно, что поршень не чувствует плавного непрерывного силой, а серией равноотстоящих ударов. Однако, если поршень сильно тяжелее частицы, это будет иметь тот же эффект, что и гладкая сила в течение длительного времени по сравнению с интервалом между ударами. Так что же значение эквивалентной гладкой силы?

Использование Ньютона закон в виде сила = скорость изменения импульса , мы видим, что импульс частицы изменяется на 2 мВ каждый раз, когда она сталкивается с поршнем. Время между число попаданий равно 2L/v, поэтому частота попаданий составляет v/2L в секунду. Это означает, что если бы не было уравновешивающая сила, то по закону сохранения импульса частица вызовет импульс поршня будет изменяться на 2mv×v/2L единиц в каждую секунду. Это скорость изменение количества движения, а значит, должно быть равно уравновешивающей силе, т. поэтому F=mv2/L.

Обобщим теперь случай, когда множество частиц отскакивает внутри прямоугольной коробки длиной L в направлении x (которое находится вдоль края коробка). Суммарная сила со стороны площади А, перпендикулярной направлению x, представляет собой просто сумму одной частицы термины, релевантная скорость представляет собой составляющую скорости в направлении x. Давление просто сила на единицу площади, P=F/A. Из Конечно, мы не знаем, каковы скорости частиц в реальном газа, а оказывается, что подробности нам и не нужны. Если мы суммируем N вкладов, по одному от каждой частицы в поле, каждый вклад пропорционален vx2 для этой частицы, сумма просто дает нам N раз среднее значение vx2. То есть

P=F/A=Nmvx2¯/LA=Nmvx2¯/V

, где N частиц в ящике объемом V. Далее мы отмечаем, что частицы одинаково вероятно, движется в любом направлении, поэтому среднее значение vx2 должно быть таким же, как среднее значение vy2 или vz2, а поскольку v2=vx2+vy2+vz2, отсюда следует, что

P=Nmv2¯/3 V.

Это удивительно простой результат! Макроскопическое давление газа относится непосредственно к средней кинетической энергии на молекулу .

Конечно, в вышесказанном мы не подумали о возможных осложнениях, вызванных взаимодействиями между частицами, но в Дело в том, что для таких газов, как воздух при комнатной температуре, эти взаимодействия очень маленький. Кроме того, это хорошо Экспериментально установлено, что большинство газов удовлетворяют газовому закону в широком диапазоне Диапазон температуры:

PV = NRT

для N N Моли газа, то есть N = N/NA, с номером Na Avogadro и R

Вводя постоянную Больцмана kB=R/NA, это легко проверить из нашего результата для давления и закона идеального газа, что средняя кинетическая энергия молекул пропорциональна абсолютной температуре ,

ЭК¯=12мв2¯=32кБТ.

Постоянная Больцмана kB= 1,38,10 ^-23 Дж/К.

Максвелл находит распределение скоростей

К 1850-м годам различные трудности с существующими теории теплоты, такие как калорическая теория, вызвали некоторое переосмысление, и люди еще раз взглянули на кинетическую теорию Бернулли, но мало реально прогресс был достигнут, пока Максвелл не занялся проблемой в 1859 г.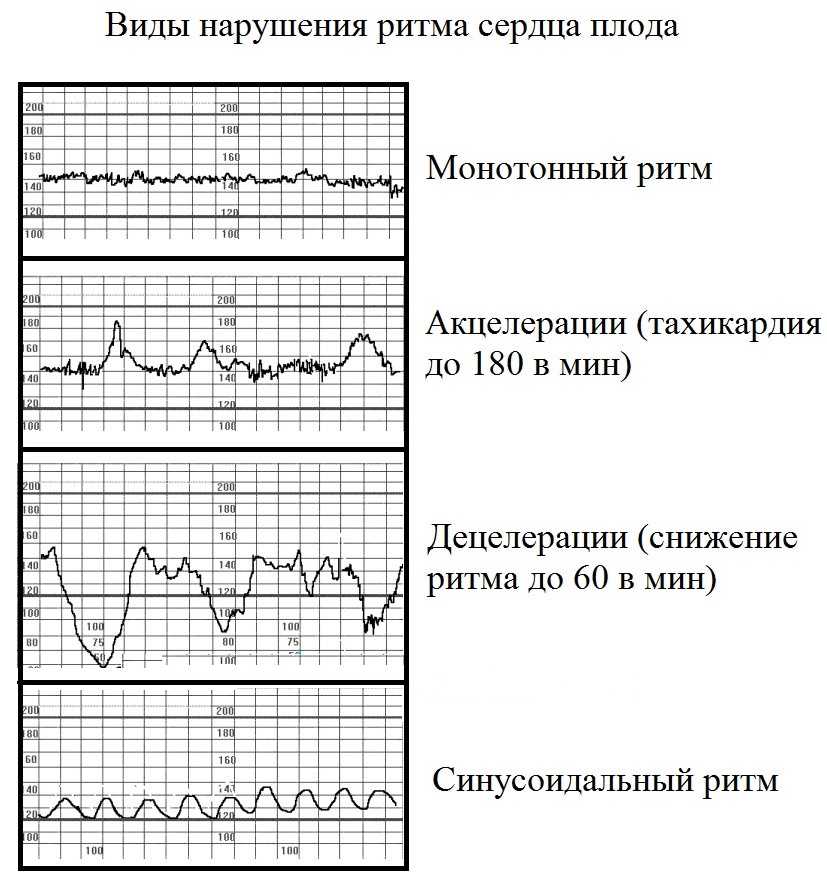 . Максвелл работал с картиной Бернулли, которая атомы или молекулы в газе были совершенно упругими частицами, подчиняющимися законам Ньютона, отскакивающими друг от друга (и от стенок контейнера) по прямолинейным траекториям в промежутках между столкновениями. (На самом деле в столкновениях присутствует некоторая неупругость с боковыми сторонами — подпрыгивающая молекула может возбуждать или девозбуждать колебания в стенке, вот как газ и контейнер приходят в тепловое равновесие.) Максвелл понял, что это было полностью безнадежно пытаться анализировать эту систему с помощью законов Ньютона, хотя это и можно было бы сделать в принципе, было слишком много переменных, чтобы начать записывать уравнения. С другой стороны, совершенно подробное описание того, как двигалась каждая молекула, на самом деле не требовалось. тем не мение. Что был нужен был какой-то понимание того, как эта микроскопическая картина связана с макроскопической свойства, которые представляли собой средние значения для огромного количества молекул.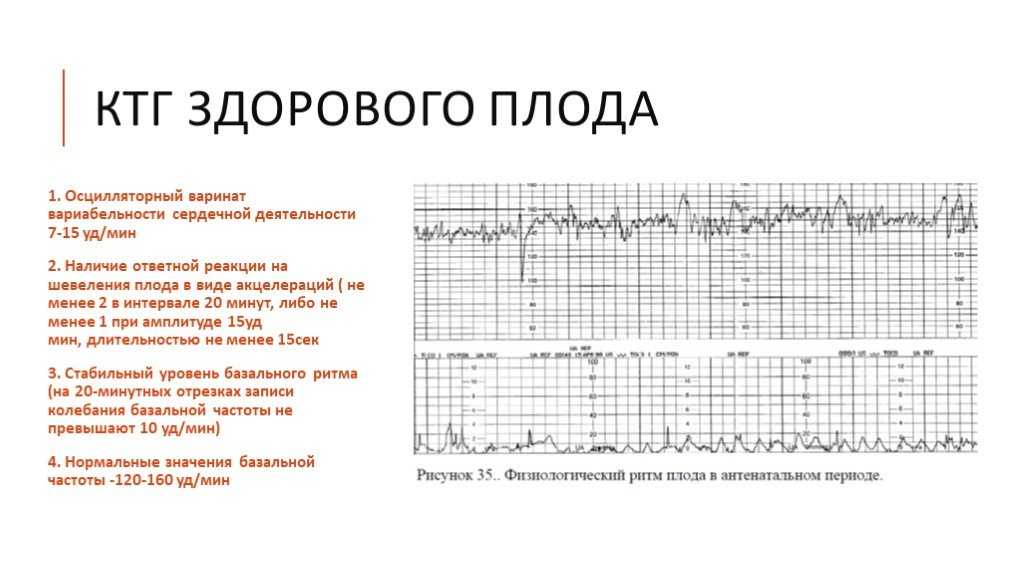

соответствующая микроскопическая информация не является знанием положения и скорости каждой молекулы в каждый момент времени, но только функция распределения , то есть какой процент молекулы находятся в определенной части сосуда, и какой процент их скорости в определенном диапазоне в каждый момент времени. Для газа в тепловом равновесии , функция распределения не зависит от времени . Игнорируя крошечные поправки на гравитацию, газ будет распределен равномерно в контейнере, поэтому единственная неизвестная скорость функция распределения.

Чтобы легко увидеть, как случайные столкновения могут привести к четко определенному распределению скорости, даже если мы начнем с того, что все молекулы имеют одинаковую скорость, проверьте этот апплет!

Пространственная скорость

Как выглядит функция распределения скоростей? Предположим, что в какой-то момент времени один конкретная молекула имеет скорость v→=(vx,vy,vz). Мы можем записать эту информацию, построив трехмерный скорость пространства , с оси vx,vy,vz и поставив точку P1 P ₁ представляет скорость молекулы (красная стрелка, конечно же, v→ ):

Теперь представьте, что в этот момент мы можем измерить скорости всех молекул в контейнер и поместите точки P2,P3,P4,…,PN в пространстве скоростей. Поскольку N порядка 10 ²¹ для 100 см3 газ, это не очень практично! Но мы можете себе представить, что получится в результате: облако точек в пространстве скоростей, равномерно распределены во всех направлениях (нет причин, по которым молекулы предпочли бы двигаться в направлении x, скажем, а не в направлении y) и истончаться при удалении от начала координат к все более и более высоким скоростям.

Теперь, если бы мы могли продолжать следить за ситуацией, как время отдельные точки будут перемещаться, поскольку молекулы отскакивают от стен, или друг друга, так что вы можете подумать, что облако немного сдвинется. Но в любой реалистичной макроскопической ситуации существует 90 583 огромного числа 90 584 молекул. и для любого контейнера разумного размера можно с уверенностью предположить, что количество молекул в любой небольшой области пространства скоростей остается практически постоянной. Очевидно, что это не может быть верным для региона. пространство скоростей настолько крошечное, что оно содержит только одну или две молекулы на средний. Но можно показать статистически, если в определенном небольшом объеме в пространстве скоростей флуктуация числа со временем имеет порядок N, поэтому область, содержащая миллион молекул, будет варьируются в числах примерно на одну тысячную, триллион молекулы на одна часть на миллион. Начиная со 100 куб.см. воздух содержит порядка 10 ²¹ молекул, мы можем на практике разделить область пространства скоростей, занимаемую газом, на миллиард ячеек, а еще имеют вариацию в каждой ячейке закажите одну часть на миллион!

Суть в том, что для макроскопического количества газа флуктуации плотности как в обычном пространстве, так и в пространстве скоростей все практические цели пренебрежимо малы, и мы можем считать, что газ равномерно распределен в обоих пространствах.

Аргумент симметрии Максвелла

Максвелл нашел функцию распределения газа по скоростям молекулы в тепловом равновесии с помощью следующего элегантного аргумента, основанного на симметрия.

Для газа из N частиц пусть количество частиц, имеющих скорость в направлении x между vx и vx+dvx равна Nf1(vx)dvx. В другими словами, f1(vx)dvx   — доля всех частиц со скоростью по оси x, лежащей в интервале между vx и vx+dvx. (Я написал f1 вместо f, чтобы помнить, что эта функция относится только к одна компонента вектора скорости.)

Если мы сложим дроби для всех возможных значений vx, результат, конечно, должен быть 1:

∫−∞∞f1(vx)dvx=1.

Но в направлении х нет ничего особенного — для газа молекул в контейнере, по крайней мере, вдали от стенок, все направления смотрят одинаково, поэтому одна и та же функция f даст распределения вероятностей в другие направления тоже. Следует сразу же, что вероятность того, что скорость находится между vx и vx+dvx , ви   и вы+двы,   и vz и vz+dvz должны быть:

Nf1(vx)dvxf1(vy)dvyf1(vz)dvz=Nf1(vx)f1(vy)f1(vz)dvxdvydvz.

Обратите внимание, что эта функция распределения при интегрировании по все возможные значения трех компонентов скорости, дает общее число частиц равно N, как и должно быть (поскольку интегрирование по каждому f1(v)dv дает единицу).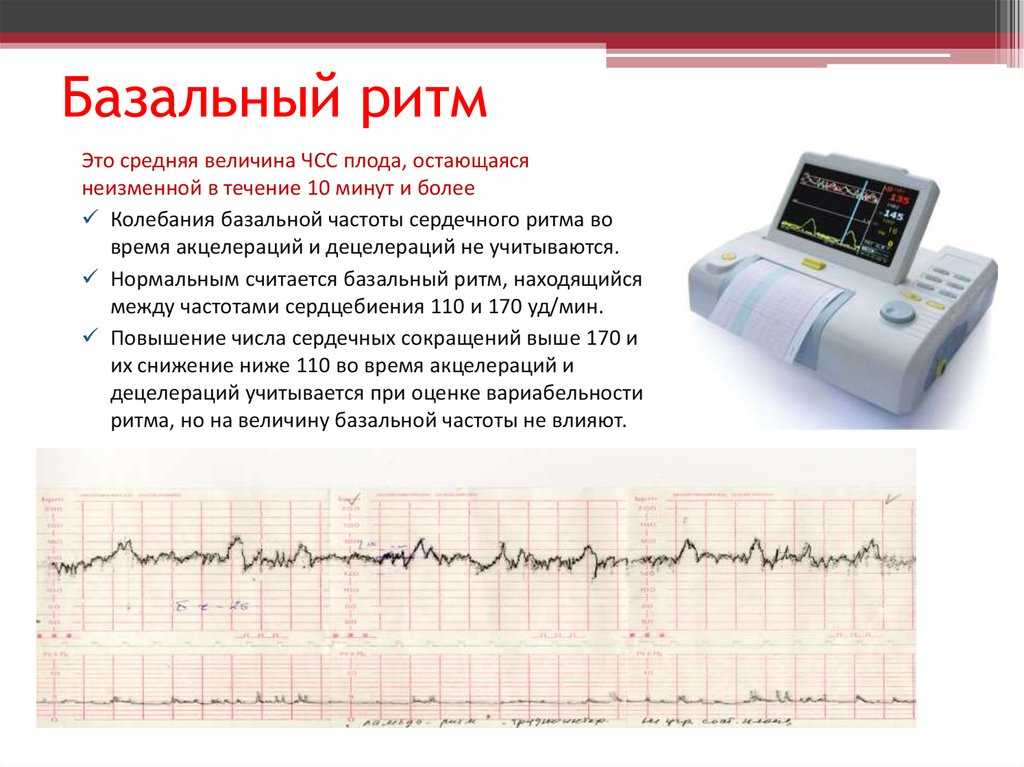

Далее следует умная часть — поскольку любой направление так же хорошо, как и любое другое направление, функция распределения должна зависеть только по полной скорости частицы, не по раздельной компоненты скорости. Следовательно, утверждал Максвелл, должно быть следующим образом:

f1(vx)f1(vy)f1(vz)=F(vx2+vy2+vz2)

, где F — другая неизвестная функция. Однако очевидно, что продукт функций слева отражается в сумме переменных на Правильно. Только так выйдет если переменные появляются в показателе степени в функциях слева. В самом деле, легко проверить, что это уравнение решается функцией вида:

f1(vx)=Ae−Bvx2.

Эта кривая называется гауссовой : центрируется в начале координат и падает off очень быстро по мере увеличения vx. Принимая A=B=1 просто для того, чтобы увидеть форму, мы находим:

. В этот момент A и B являются произвольными константами — мы будем в конечном итоге найти их значения для реальной пробы газа при заданном температура. Обратите внимание, что (после Максвелл) мы поставили знак минус в показателе степени, потому что в конце концов быть все меньше и меньше частиц при переходе к более высоким скоростям, конечно, не расходящееся число.

Перемножение распределений вероятностей для трех направлений дает распределение по скорости частиц v, где v2=vx2+vy2+vz2. Так как все направления скорости одинаково вероятно, ясно, что естественная функция распределения такова, что дает число частиц, имеющих 90 583 скорость 90 584 между v  и v+dv.

Из приведенного выше графика видно, что наиболее вероятное значение vx равно нулю. Если бы молекулы газа были ограничены одним измерением, просто двигаясь назад и далее по строке, то наиболее вероятное значение их скорость будет также нуль. Однако для молекул газа, свободных двигаться в двух или трех измерениях, наиболее вероятное значение скорости , а не ноль. Проще всего это увидеть в двухмерном пример. Предположим, мы наносим точки P представляющие скорости молекул в области вблизи начала координат, поэтому плотность точек не сильно зависит от протяженности нашего графика (мы остаемся около вершины пика на одномерной кривой, показанной выше).

Теперь разделим двумерное пространство на регионы соответствующие равным приращениям скорости:

0 до Δv, Δv до 2Δv, 2Δv до 3Δv,…

в кольцевые области между окружностями, последовательные радиусы которых разнесены на Δv :

Каждая из этих кольцевых областей соответствует одной и той же скорости приращение Δv. В частности, зеленая зона между круг радиусом 8Δv и один радиусом 9Δv соответствует тому же приращению скорости 90 583 90 584, что и маленький красный кружок в середине, который соответствует скоростям между 0 и Δv. Следовательно, если молекулярные скорости довольно равномерно распределены в этой области плоскости (vx,vy), близкой к исходной, будет намного больше молекул с скорости между 8Δv и 9Δv, чем между 0 и Δv, поэтому , скорее всего, скорость будет , а не , равной нулю. Чтобы узнать, что это на самом деле, мы должны поместите этот аргумент площади вместе с падением плотности по Гауссу при переходе далеко от истока. мы обсудим это вскоре.

Тот же аргумент работает и в трех измерениях — просто немного сложнее визуализировать. Вместо концентрических окружностей имеем концентрические сферы. Все точки, лежащие на сферическая поверхность с центром в начале координат соответствует той же скорости.

Теперь выясним распределение частиц как функция скорости. Распределение в трехмерное пространство (vx,vy,vz) из анализа Максвелла dvxdvydvz=NA3e−Bv2dvxdvydvz

Чтобы перевести это в число частиц, имеющих скорость между v и v+dv, нам нужно выяснить, сколько этих маленьких коробки dvxdvydvz там соответствующие скорости между v  и v+dv. Другими словами, что такое объем пространства скоростей между двумя соседних сфер, обе с центром в начале координат, внутренняя с радиусом v, внешняя бесконечно малая, с радиус v+dv? С dv настолько мал, что этот объем равен площади сфера, умноженная на dv: то есть 4πv2dv.

Наконец, распределение вероятностей как функция скорость:

f(v)dv=4πv2A3e−Bv2dv.

Конечно, наша работа не окончена — мы еще есть эти две неизвестные константы A и В . Однако так же, как для функции f1(vx),  f(v)dv является долей молекул, соответствующих скоростям между v и v+dv, и все эти доли, взятые вместе в сумме должно давать 1.

То есть

∫0∞f(v)dv=1.

Нам нужен стандартный результат ∫0∞x2e−Bx2dx=(1/4B)π/B (вывод можно найти в моих 152 Notes по экспоненциальным интегралам) и найти:

4πA314BπB=1.

Это означает, что на самом деле существует только одна произвольная переменная слева: если мы можем найти B, это уравнение дает нам A: то есть 4πA3=4πB3/2, а 4πA3 — это то, что появляется в f(v).

Глядя на f(v), мы замечаем, что B является мерой того, насколько далеко распределение спреды от начала координат: если B мало, распределение падает больше медленно — средняя частица более энергична. Напомним теперь, что средняя кинетическая энергия частиц связана до температуры на 12мВ2¯= 32кВт.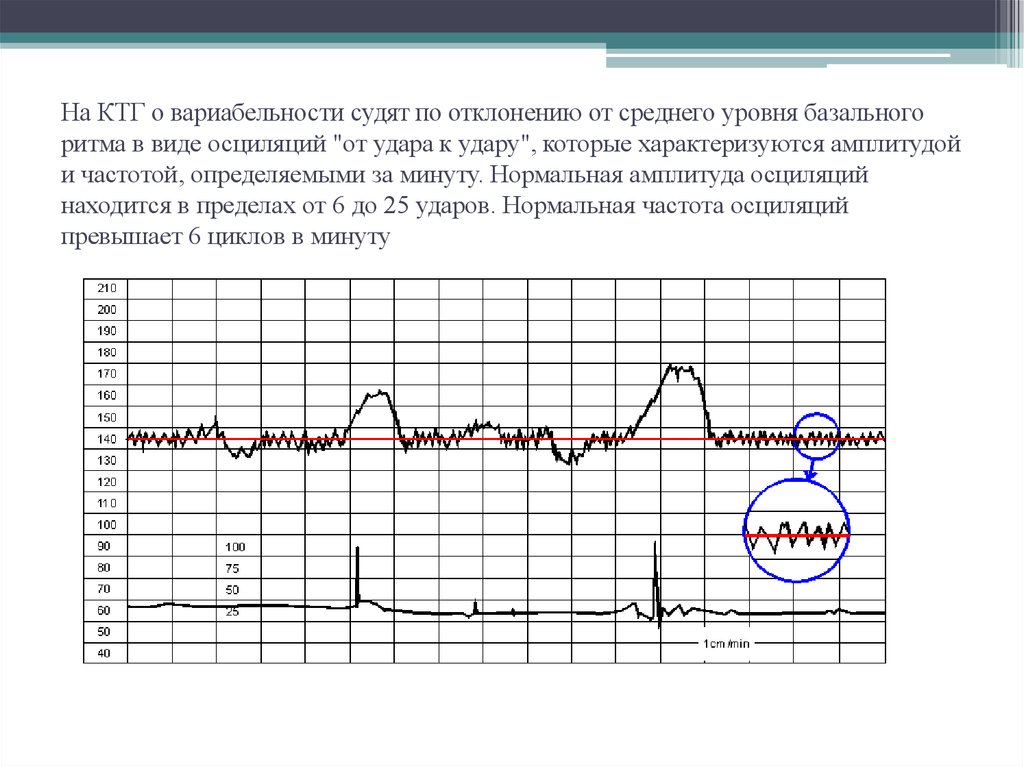 Это означает, что B связана с обратной температурой.

На самом деле, поскольку f(v)dv — это доля частиц в интервале dv при v, и эти частицы имеют кинетическую энергию 12mv2, мы можем использовать распределение вероятностей для найти среднюю кинетическую энергию, приходящуюся на одну частицу:

12mv2¯=  ∫ 0 ∞12mv2f(v)dv.

Чтобы вычислить этот интеграл, нам понадобится еще один стандартный результат: ∫0∞x4e−Bx2dx=(3/8B2)π/B. Находим:

12mv2¯= 3m4B.

.Подставляя значение средней кинетической энергии в с точки зрения температуры газа,

12mv2¯= 32kBT

дает B=m/2kBT, поэтому 4πA3=4πB3/2=4π(m2πkBT)3/2.

Это означает функцию распределения

f(v)=4π(m2πkBT)3/2v2e−mv2/2kT=4π(m2πkBT)3/2v2e−E/kT

, где E — кинетическая энергия молекулы.

Обратите внимание, что эта функция параболически увеличивает от нуля для низких скоростей, а затем округляет до достижения достигает максимума и, наконец, убывает экспоненциально.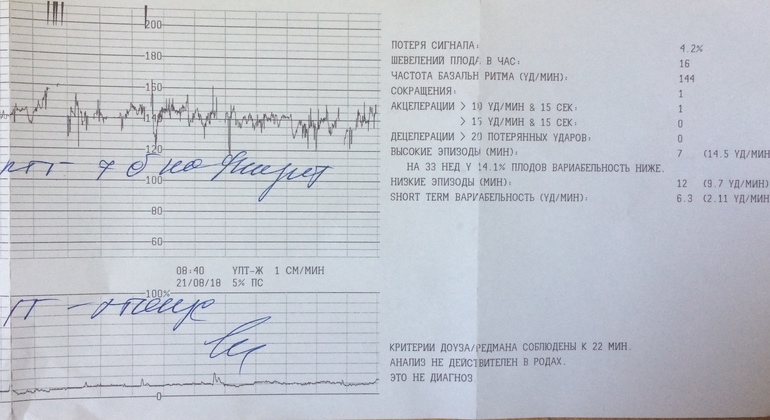 При повышении температуры положение максимума смещается в сторону Правильно. Общая площадь под кривой всегда равна единице по определению. Для молекул воздуха (скажем, азота) при комнатной температура кривая синяя ниже. Красный для абсолютного температура понизилась в два раза:

А как насчет потенциальной энергии?

Анализ Максвелла решает проблему нахождения статистическое распределение скоростей молекул идеального газа в ящике при определенная температура T: относительная вероятность того, что молекула скорость v→ пропорциональна e−mv2/2kT=e−E/kT. позиция распределение считается равномерным: молекулы считаются одинаково скорее всего где-нибудь в коробке.

Но как влияет на это распределение, если на самом деле есть какой-то потенциал, притягивающий молекулы к одному концу ящика? На самом деле, мы уже решили эту проблему, в обсуждении ранее в изотермической атмосфере. Рассмотрим действительно большой ящик высотой в километры, поэтому воздух будет значительно плотнее внизу. Предположим, что температура везде одинакова. Мы нашли при этих условиях, что с законом Бойля, выраженным в виде

ρ=CP

плотность атмосферы изменялась с высотой как

P=P0e−Cgh или, что эквивалентно, ρ=ρ0e−Cgh.

Теперь мы знаем, что закон Бойля — это всего лишь фиксированная температура. вариант Закона о газах PV=nRT, и плотность

ρ= масса/объем =Nm/V

, где N – общее число молекул, а m – молекулярная масса,

CP=ρ=Nm/V.

Перестановка,

PV=Nm/C=nNAm/C,

для n молей газа, каждый моль содержит Авогадро число молекул NA.

Объединив это с газовым законом,

PV=nNAm/C=nRT,

, поэтому

C=NAm/RT=m/kBT

, где постоянная Больцмана kB=R/NA, как обсуждалось ранее.

Таким образом, зависимость плотности газа от высоты может быть написано

ρ=ρ0e−Cgh=ρ0e−mgh/kBT.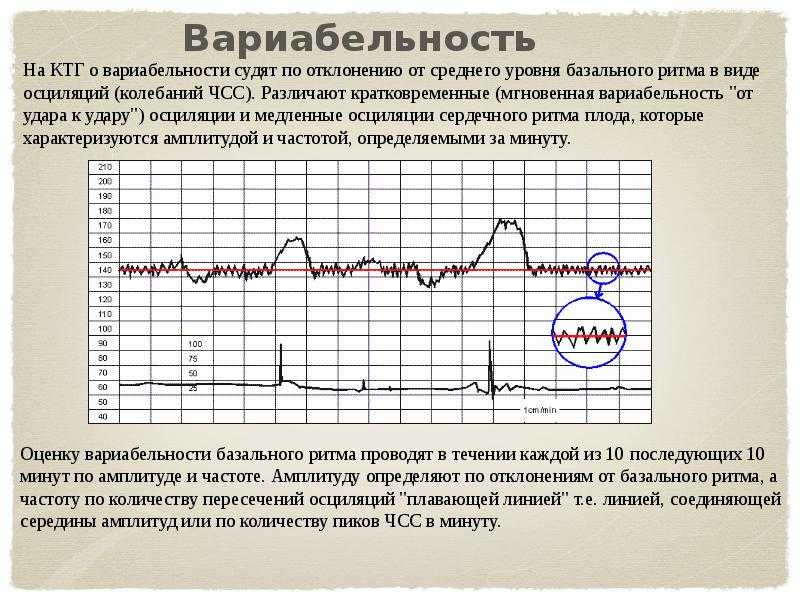

Важным моментом здесь является то, что mgh – это потенциальная энергия молекулы, а найденное нами распределение точно параллельно максвелловской скорости распределение, потенциальная энергия теперь играет роль, которую кинетическая энергия играл в таком случае.

Теперь мы готовы вычислить скорость Максвелла. распределения с этим распределением высоты, чтобы узнать, как молекулы распределены в атмосфере, и в пространстве скоростей и в обычном пространство. Другими словами, в шестимерном -мерном пространстве!

Наш результат:

f(x,y,z,vx,vy,vz)=f(h,v)∝e−mv2/2kBTe−mgh/kT=e−((1/2)mv2+ mgh)/kBT=e-E/kBT.

 То есть вероятность того, что молекула имеет всего энергия E пропорциональна e-E/kBT.

Это распределение Больцмана или Максвелла-Больцмана. Это оказывается правильным для любого типа потенциальная энергия, в том числе возникающая за счет сил между молекулами сами себя.

Степени свободы и равнораспределение энергии

Под «степенью свободы» мы подразумеваем способ, которым молекула свободно двигаться и, таким образом, иметь энергию — в этом случае, только направления x, y и z. Больцман переформулировал анализ Максвелла в терминах степеней свободы, утверждая, что средняя энергия 12kBT в каждой степени свободы, чтобы дать общее средняя кинетическая энергия 32kBT, поэтому удельная теплоемкость на молекулу предположительно составляет 1,5 кБ, а учитывая, что кВ = R/NA, удельная теплоемкость на моль получается равной 1,5 Р. В на самом деле это подтверждается экспериментально для одноатомных газов. Однако установлено, что двухатомные газы могут имеют удельную теплоемкость 2,5R и даже 3,5R. Это не трудно понять — эти молекулы имеют больше степеней свободы. Молекула-гантель может вращаться примерно в двух направлениях, перпендикулярных ее ось. Двухатомная молекула также может вибрировать. Такая простая гармоника колебательное движение обладает как кинетической, так и потенциальной энергией, и оказывается имеют полную энергию kBT в тепловом равновесии. Таким образом, разумные объяснения удельные теплоемкости различных газов можно составить, предполагая, что вклад каждой степени свободы составляет 12 КБ.