Кардиотокография (КТГ) — «Экзамен на находчивость мамы по получению высокого балла на КТГ. Или все таки достоверная процедура?! »
Привет, друзья!
У меня сейчас третья беременность. Что такое КТГ уже знаю. Помню,что перед процедурой зачастую рекомендуют скушать шоколадку, чтобы ребенок был активнее.
Недавно на 36 неделе я ходила на КТГ повторно, потому что за 10 дней до этого моя малышка в животе спала во время процедуры.
- ЧТО ТАКОЕ КТГ?
Сначала процедура КТГ для меня была непонятна. Приходишь в кабинет, тебе на живот кладут датчик округлой формы, в руку дают устройство с кнопкой и нужно нажимать на кнопку, как только почувствуешь шевеления ребенка. В это время на мониторе прибора фиксируется пульс ребенка, а из прибора «выползает» бумага, так же как во время кардиограммы.
Кардиотокография (КТГ) — это метод оценки состояния плода, заключающийся в регистрации и анализе частоты его сердцебиения в покое, движении, при сокращениях матки и воздействии различных факторов среды
За аббревиатурой КТГ скрывается исследование, которое называется кардиотокографией.
По своей сути оно представляет собой постоянную, непрерывную регистрацию сердечных сокращений малыша, маточных сокращений, а также двигательной активности ребенка. Все эти параметры фиксируются синхронно и сразу в режиме реального времени записываются самописцем или компьютерной программой на калибровочную ленту.
КТГ позволяет узнать, как чувствует себя ребенок. В первую очередь, аппарат фиксирует и показывает ЧСС (частоту сердечных сокращений) – основной параметр, который позволяет судить о самочувствии крохи. Ультразвуковой датчик, работающий на основе эффекта Доплера, посылает ультразвуковую волну. Она отражается от тканей и движущихся клеток крови в кровеносных сосудах и отправляется обратно, к датчику. В результате
становится очевидно, с какой частотой бьется маленькое сердце.
В интернете много информации о назначении данной процедуры.
Своими словами скажу — КТГ показана всем беременным на последних неделях беременности для оценки состояния плода.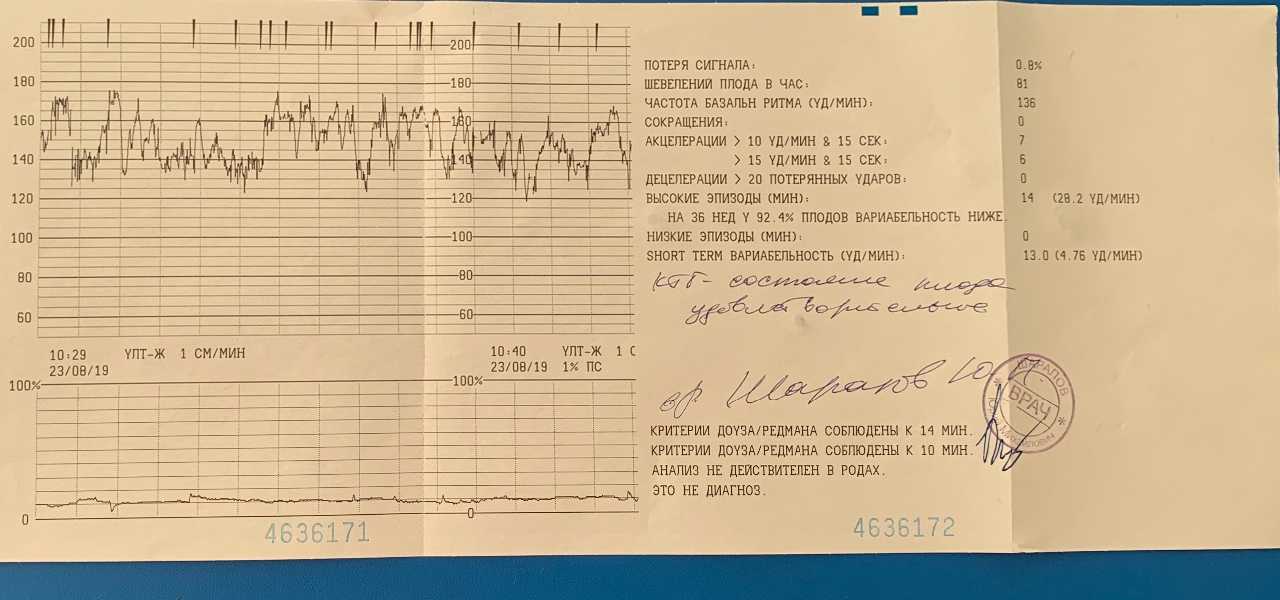 Врач оценивает это состояние в баллах. В норме это не менее 8 баллов. Если ниже, то гинеколог назначает лекарства, но предварительно направляет на повторное КТГ.
Врач оценивает это состояние в баллах. В норме это не менее 8 баллов. Если ниже, то гинеколог назначает лекарства, но предварительно направляет на повторное КТГ.
- МОЙ ОПЫТ.
Течение моей третьей беременности не доставляло мне опасений за ребенка, анализы лучше чем в предыдущие две беременности, состояние отличное, ребенок активный в меру.
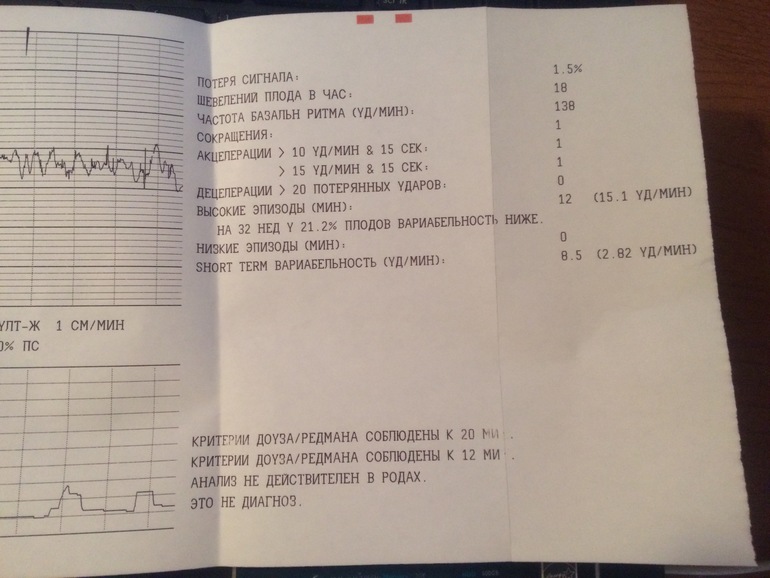
И вот съев шоколадку в первой половине дня я отправилась на КТГ. Почти всю процедуру — которая занимает 30 минут, ребенок спал в животе и у меня не вышло ее разбудить. Датчик к тому же к животу мне не закрепили, а сказали удерживать рукой.
Так вот, полусидя-полулежа на кушетке с вытянутыми ногами, я одной рукой прижимаю датчик к области пупка, а другой рукой держу кнопку, чтобы фиксировать движения ребенка. Через 10 минут такого сидения затекла поясница и пятая точка, пальцы занемели удерживать датчик на животе. а стоило усилить или ослабить нажатие, как монитор переставал фиксировать сердцебиение ребенка.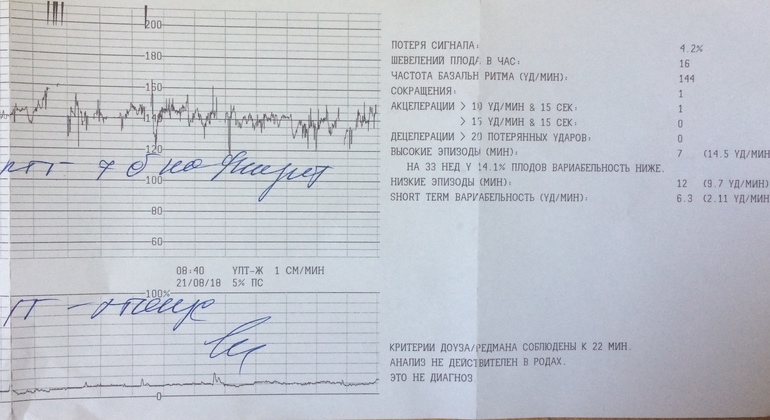
Доктор, изучив данные поставила 7 баллов.
КТГ 7 баллов – такая оценка считается показателем начала кислородной недостаточности плода. В данном состоянии специалист назначает соответственное лечение, чтобы избежать возникновение гипоксии, а также для улучшения состояния малыша при ее наличии. При оценке в 7 баллов на 32 неделе лечебные мероприятия начинают проводить без замедления. Врач, который наблюдает за течением беременности, может в срочном порядке, отправить женщину на стационарное лечение или ограничится капельницами на дневном стационаре.
Мой гинеколог, естественно отправила меня на повторное КТГ через 10 дней.
Теперь я съела шоколадку по больше и во время процедуры много ерзала и пощипывала живот. Плюс старалась принимать разные позы — то на бок, то на другой. Ребенку видимо было не комфортно в таких условиях и она искала удобную позу — теперь она шевелилась активно. Результат — 8-9 баллов!
КТГ 8 баллов показывает нижнюю границу нормы, и такое состояние плода обычно не требует ни проведения лечебных мероприятий, ни госпитализации.
Нормальными значениями считается оценка 9 и 10 баллов. Данные показатели могут означать одно, что развитие плода проходит хорошо, без развития патологий.
- ИТОГ.
Вот вроде бы необходимая процедура, но как оказалось в моем случае — если я не проявлю смекалку, то могу получить ненужное мне лечение. А каково первородящим и впечатлительным мамам!? Процедура вроде бы показательная, но зависящая от многих факторов.
А каково первородящим и впечатлительным мамам!? Процедура вроде бы показательная, но зависящая от многих факторов.
Поэтому плюсую за:
+ доступность
+ быстрый результат
+ информативность
+ оценка состояния плода
+ безболезненно
+ безопасно
Но минусы стоит учитывать в первую очередь:
— влияние многих факторов на оценку состояния ребенка
— неудобно долго сидеть в одном положении
— не всегда достоверный результат
КТГ конечно РЕКОМЕНДУЮ, но прошу учитывать описанный мной опыт и факторы! А еще не поддаваться страхам и задавать вопросы врачам обязательно!!! Всем здоровья и добра!
Еще отзывы на медицинскую тематику:
Средства д/лечения простуды и гриппа Линкас
УЗИ (Ультразвуковое исследование) молочных желез
Энтеросорбенты Активированный уголь
Средства для лечения желудочно-кишечного тракта Смекта
Естественные роды
КТ Грудной клетки
КТГ при беременности — что это?
КТГ плода – это методика синхронной и непрерывной фиксации частоты сердечных сокращений ребенка в утробе матери и изменений тонуса матки.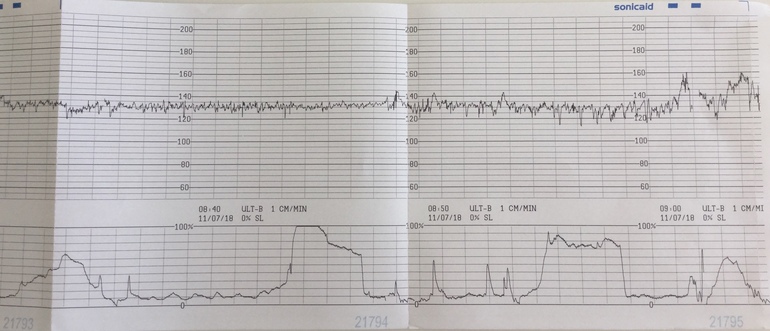 Проводится с помощью аппарата УЗИ с эффектом Доплера и тензиометрического датчика для фиксации сокращений матки. Результаты записываются на графическую ленту либо изображаются на мониторе с дальнейшим сохранением в памяти компьютера, КТГ расшифровка проводится в баллах с использованием специальной шкалы. Обследование позволяет сделать вывод о состоянии плода, выявить признаки гипоксии в последнем триместре беременности и в родах. Процедура безопасная и может проводиться по показаниям даже ежедневно.
Проводится с помощью аппарата УЗИ с эффектом Доплера и тензиометрического датчика для фиксации сокращений матки. Результаты записываются на графическую ленту либо изображаются на мониторе с дальнейшим сохранением в памяти компьютера, КТГ расшифровка проводится в баллах с использованием специальной шкалы. Обследование позволяет сделать вывод о состоянии плода, выявить признаки гипоксии в последнем триместре беременности и в родах. Процедура безопасная и может проводиться по показаниям даже ежедневно.
Когда проводится КТГ
Проводить КТГ при беременности можно уже с 28-30 недель, но наиболее информативным исследование становится после 32 недели. При нормальном состоянии матери и плода исследование в третьем триместре рекомендуют делать приблизительно раз в десять дней. Когда есть показания, его делают чаще, раз в 5-7 дней, а при необходимости ежедневно.
- Отрицательный резус у матери
- Наличие в анамнезе выкидышей, замирания беременности, мертворождений
- Снижение активности ребенка по мнению матери
- Патологии плода, выявленные при УЗИ (задержка развития, нарушения плацентарного кровотока, аномалии пуповины и плода, снижение количества движений, изменения в околоплодных водах)
- Гестоз последнего триместра
- Предлежание плаценты или неправильное предлежание плода
- Многоплодие, маловодие, многоводие
- Перенашивание беременности
- Экстрагенитальные патологии у женщины (сахарный диабет и другие эндокринные болезни, патологии сердца и сосудов, анемия, инфекционные заболевания с повышением температуры).

Проводят плановое КТГ неделям ближе к 32-34, внеплановые по особым показаниям могут делать раньше, уже с 28 недель с последующими регулярными повторениями. Поскольку методика безопасная, повторять обследование можно практически ежедневно, оно не нанесет вреда ни матери, ни ребенку.
Как проводят КТГ плода
Особой подготовки для проведения КТГ неделям к тридцати не требуется. Рекомендуют делать исследование в периоды наибольшей активности плода, с девяти утра до двух часов дня, а также с семи вечера до полуночи. Не желательно КТГ проводить натощак, а также на полный желудок или сразу после введения глюкозы. Оптимальное время – через час или полтора после еды.
Различают два разных вида КТГ при беременности – прямое и непрямое. Прямая кардиотокография проводится редко и только в родах при нарушении целостности плодного пузыря. Делают ее с помощью специального спиралевидного игольчатого спиралевидного датчика, который вводят в предлежащую часть плода.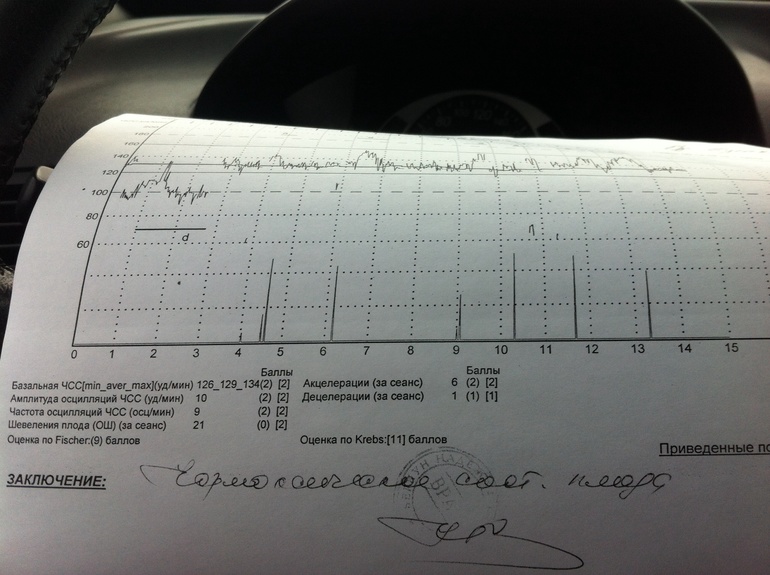 Тонус матки измеряют с помощью катетера, который вводится в полость матки. Непрямая КТГ плода делается через переднюю стенку живота. Используют два датчика – один прикрепляется в месте наилучшей слышимости сердцебиений (врач определяет его с помощью стетоскопа перед обследованием), другой – в правом угле дна матки.
Тонус матки измеряют с помощью катетера, который вводится в полость матки. Непрямая КТГ плода делается через переднюю стенку живота. Используют два датчика – один прикрепляется в месте наилучшей слышимости сердцебиений (врач определяет его с помощью стетоскопа перед обследованием), другой – в правом угле дна матки.
Проводят КТГ в положении женщины сидя или на правом боку. Укладывать беременную на спину не советуют, так как при этом могут пережиматься магистральны кровеносные сосуды и КТГ расшифровка будет некорректной. Среднее время проведения процедуры – 40 минут. При нормальном ритме у плода КТГ можно сократить до 15-20 минут. В родах продолжительность исследования должна быть не менее двадцати минут, или пяти схваток.
Первые десять минут измеряют базовый ритм, такое КТГ плода называется нестрессовым. Его дополняют фиксацией шевелений плода (с помощью датчика или по словам беременной). Затем переходят к функциональным пробам или стрессовому КТГ. Для изучения сердцебиения ребенка в утробе матери используют следующие тесты:
- Окситоциновый тест
- Маммарный тест
- Акустический тест
- Пальпация плода
- Рефлекторные пробы
Окситоциновый тест проводится в основном перед родами и в условиях стационара. С помощью окситоцины у женщины провоцируют схватки и делают КТГ плода при усиленных сокращениях матки, проводится обследование редко. Маммарный тест по своей сути похож на окситоциновый, но более безопасный. Беременная стимулирует пальцами соски, что вызывает усиление маточных сокращений. Противопоказан тест при повышенном тонусе и угрозе преждевременных родов. При акустическом тесте КТГ фиксирует изменение сердцебиений плода при воздействии звукового раздражителя. Во время пальпации плода немного смещают его предлежащую часть. Рефлекторные пробы делают редко. Функциональные пробы, которые изменяют параметры плацентарного кровотока, и атропиновый тест сейчас уже не применяются.
С помощью окситоцины у женщины провоцируют схватки и делают КТГ плода при усиленных сокращениях матки, проводится обследование редко. Маммарный тест по своей сути похож на окситоциновый, но более безопасный. Беременная стимулирует пальцами соски, что вызывает усиление маточных сокращений. Противопоказан тест при повышенном тонусе и угрозе преждевременных родов. При акустическом тесте КТГ фиксирует изменение сердцебиений плода при воздействии звукового раздражителя. Во время пальпации плода немного смещают его предлежащую часть. Рефлекторные пробы делают редко. Функциональные пробы, которые изменяют параметры плацентарного кровотока, и атропиновый тест сейчас уже не применяются.
КТГ при беременности можно проводить на разной аппаратуре. Раньше в большинстве клиник использовали приборы, которые записывали сердцебиения и сокращения матки на бумаге, расшифровку врач проводил самостоятельно. Это требовало высокой квалификации и опыта специалиста. Сейчас все больше используется аппаратура с компьютерной расшифровкой, это позволяет получать более достоверные результаты. Также появились возможности проводить КТГ по неделям в режиме онлайн. Специальные датчики прикрепляют к коже живота, сигнал через смартфон передается на монитор компьютера, где врач имеет возможность следить за изменениями сердечной деятельности плода.
Также появились возможности проводить КТГ по неделям в режиме онлайн. Специальные датчики прикрепляют к коже живота, сигнал через смартфон передается на монитор компьютера, где врач имеет возможность следить за изменениями сердечной деятельности плода.
КТГ — расшифровка
Показателями КТГ плода являются частота сердцебиений, базовая частота ЧСС и ее вариабельность, акцелерации и децелерации. Акцелерациями называют ускорение частоты сердечных сокращений на 15 и более ударов, в течение 15 секунд и дольше. Децелерации – замедление ЧСС на такое же количество ударов в аналогичный промежуток времени. В норме КТГ расшифровка фиксирует частоту сердечных сокращений плода на уровне 120-160 ударов в минуту, вариабельность ее составляет 5-25 ударов. Децелерации должны отсутствовать или быть редкими и неглубокими. Акцелераций может быть две и больше на протяжении десяти минут.
КТГ расшифровка проводится по трехбалльной системе, результат оценивают цифрами от нуля до двух.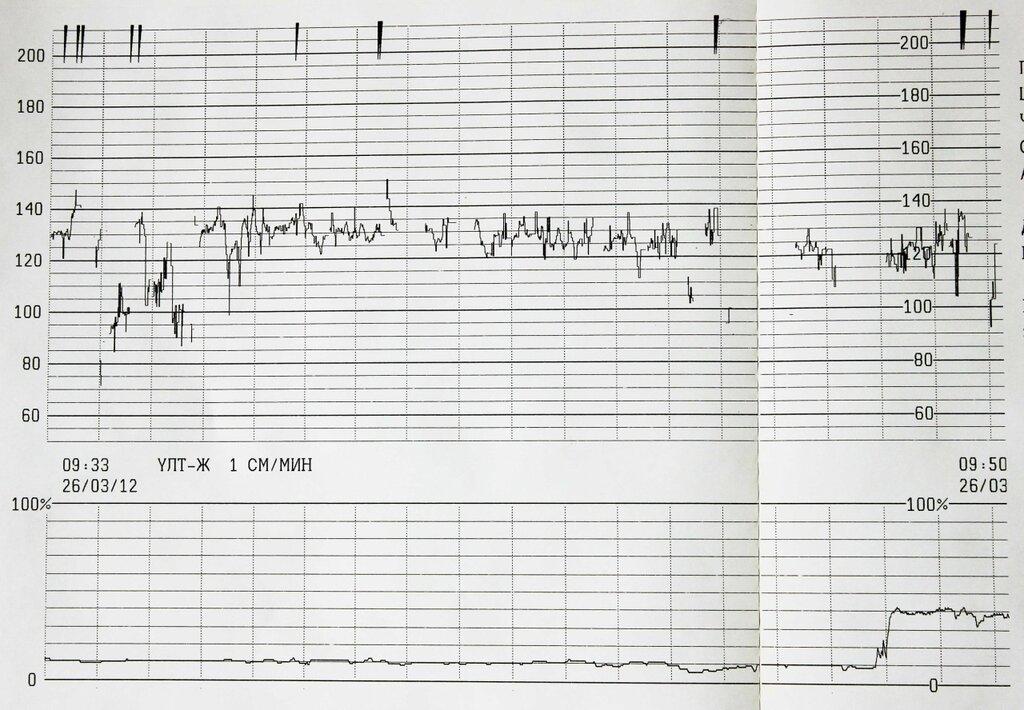 При измерении базального ритма ноль баллов присваивается, если ЧСС плода ниже 100 ударов в минуту или выше 180 ударов. Один балл – при ЧСС 100-120 или 160-180 ударов. Два балла – при нормальном количестве сокращений, в пределах 120-160 в минуту. При амплитуде сокращений меньше 3, фиксируют 0 баллов, при амплитуде 3-6 ударов – 1 балл, при нормальной амплитуде 5-15 ударов – 2 балла. Если акцелерации не выявлены, КТГ расшифровка оценивается в 0 баллов, при 1-4 акселерациях (единичных либо периодических) присваивают 1 балл, при 5 и больше единичных ускорениях ритма дают 2 балла. Наличие поздних тяжелых или атипичных децелераций оценивается в 0 баллов, ранние тяжелые и вариабельные замедления оцениваются в 1 балл, отсутствие децелераций или легкие вариабельные замедления ритма оценивают в 2 балла. Также шкала КТГ по неделям включает оценку шевелений плода. Их отсутствие – 0 баллов, 1-3 шевеления – 2 балла, 3 и больше шевелений – 2 балла.
При измерении базального ритма ноль баллов присваивается, если ЧСС плода ниже 100 ударов в минуту или выше 180 ударов. Один балл – при ЧСС 100-120 или 160-180 ударов. Два балла – при нормальном количестве сокращений, в пределах 120-160 в минуту. При амплитуде сокращений меньше 3, фиксируют 0 баллов, при амплитуде 3-6 ударов – 1 балл, при нормальной амплитуде 5-15 ударов – 2 балла. Если акцелерации не выявлены, КТГ расшифровка оценивается в 0 баллов, при 1-4 акселерациях (единичных либо периодических) присваивают 1 балл, при 5 и больше единичных ускорениях ритма дают 2 балла. Наличие поздних тяжелых или атипичных децелераций оценивается в 0 баллов, ранние тяжелые и вариабельные замедления оцениваются в 1 балл, отсутствие децелераций или легкие вариабельные замедления ритма оценивают в 2 балла. Также шкала КТГ по неделям включает оценку шевелений плода. Их отсутствие – 0 баллов, 1-3 шевеления – 2 балла, 3 и больше шевелений – 2 балла.
КТГ расшифровка считается нормальной, если суммарная оценка ее составляет 9-12 баллов. В такой ситуации проводят только динамическое наблюдение за беременной. Когда количество баллов 6-8, диагностируют гипоксию плода, без угрозы его жизни в ближайшие сутки. КТГ плода повторяют на следующий день. Если кардиотокограмма оценивается в 0-5 баллов, значит существует угроза внутриутробной гибели плода и необходимо срочное родоразрешение.
В такой ситуации проводят только динамическое наблюдение за беременной. Когда количество баллов 6-8, диагностируют гипоксию плода, без угрозы его жизни в ближайшие сутки. КТГ плода повторяют на следующий день. Если кардиотокограмма оценивается в 0-5 баллов, значит существует угроза внутриутробной гибели плода и необходимо срочное родоразрешение.
Что делать, если КТГ расшифровка неудовлетворительная
Когда КТГ расшифровка оценивается в 6-8 баллов, проводят повторное исследование, а также УЗИ и доплерографию. В комплексе эти исследования помогают выявить такие патологии, как фетоплацинтарная недостаточность, преждевременное старение плаценты, внутриутробное инфицирование, многоводие либо маловодие, угрозу преждевременных родов. В таких ситуациях беременной предлагают лечь в стационар на лечение.
Терапия при неудовлетворительной КТГ неделям к 32-34 направлена на улучшение кровоснабжение между матерью и плодом. Она предусматривает режим полного покоя для женщины и медикаментозное лечение.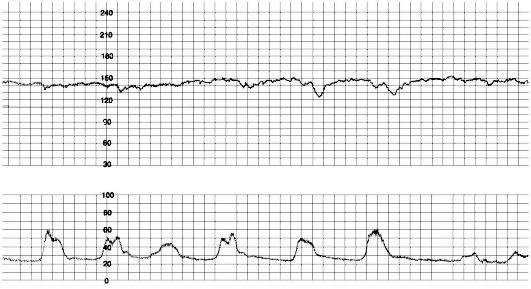 Если зафиксировано повышение тонуса матки, назначают спазмолитики (но-шпу, магнезию, папаверин), магне В6 (комплекс витаминов В), бриканил, генипрал. Для улучшения снабжения клеток кислородом используют витамина С, Е, эсенциале, глутаминовую кислоту, нейропротекторы и ангиопротекторы, внутривенное введение глюкозы, специальные кислородные коктейли. Чтобы снизить свертываемость крови, назначают аспирин, трентал, курантил, актовегин, внутривенно капают реополиглюкин. также проводят терапию сопутствующих патологий у женщин. После улучшения показателей КТГ беременную могут выписать в домой или оставить в стационаре под наблюдением до родов.
Если зафиксировано повышение тонуса матки, назначают спазмолитики (но-шпу, магнезию, папаверин), магне В6 (комплекс витаминов В), бриканил, генипрал. Для улучшения снабжения клеток кислородом используют витамина С, Е, эсенциале, глутаминовую кислоту, нейропротекторы и ангиопротекторы, внутривенное введение глюкозы, специальные кислородные коктейли. Чтобы снизить свертываемость крови, назначают аспирин, трентал, курантил, актовегин, внутривенно капают реополиглюкин. также проводят терапию сопутствующих патологий у женщин. После улучшения показателей КТГ беременную могут выписать в домой или оставить в стационаре под наблюдением до родов.
Когда КТГ неделям к 36-38 показывает низкие баллы, от нуля до пяти, беременную немедленно направляют в стационар. При таких показателях показано кесарево сечение. Если срок меньше 36 недель, пациентке могут назначить короткий курс дексаметазона, чтобы стимулировать развитие дыхательной системы ребенка. После рождения ребенка ему дополнительно вводят сурфактант, может понадобиться немедленная реанимация, и врачи должны быть к этому готовы.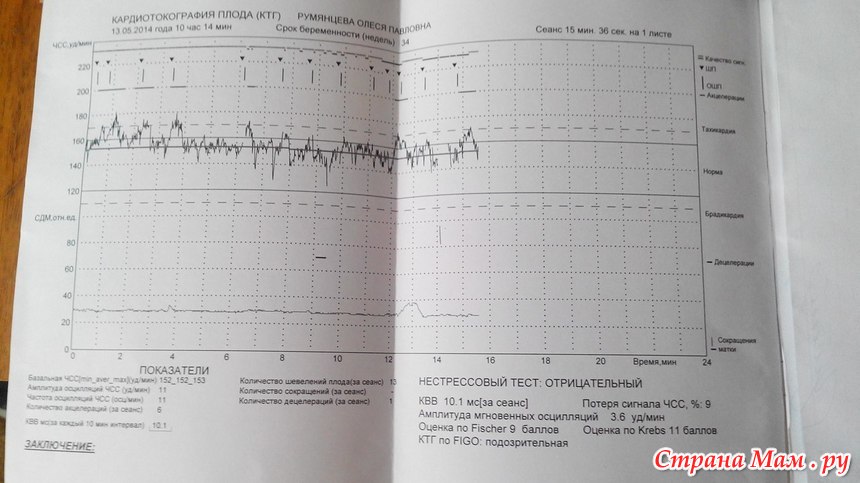
9.13: Кинетическая теория газов. Постулаты кинетической теории
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49454
- Эд Витц, Джон В. Мур, Джастин Шорб, Ксавьер Прат-Ресина, Тим Вендорф и Адам Хан
- Цифровая библиотека химического образования (ChemEd DL)
В других разделах упоминалось, что многие свойства твердых тел, жидкостей и газов можно было бы объяснить, если бы мы предположили, что вещества состоят из атомов или молекул, находящихся в постоянном движении. Закон Бойля и другие газовые законы теперь дали нам гораздо больше количественной информации о газах, и стоит спросить, можем ли мы с помощью предыдущей модели делать количественные предсказания в соответствии с этими законами. Отвечая на этот вопрос, мы также получим важные сведения о природе температуры и тепловой энергии.
Отвечая на этот вопрос, мы также получим важные сведения о природе температуры и тепловой энергии.
Микроскопическая теория поведения газа, основанная на молекулярном движении, называется кинетической теорией газов . Его основные постулаты перечислены в таблице 1:
ТАБЛИЦА \(\PageIndex{1}\) Постулаты кинетической теории газов.
1 Молекулы газа маленькие и очень далеко друг от друга. Большую часть объема, который занимает газ, составляет пустое пространство.
2 Молекулы газа находятся в постоянном беспорядочном движении. Точно так же много молекул движется в одном направлении, как и в любом другом.
3 Молекулы могут сталкиваться друг с другом и со стенками сосуда. Столкновения со стенками объясняют давление газа.
4 При столкновении молекулы не теряют кинетической энергии; то есть столкновения называются совершенно упругими . Суммарная кинетическая энергия всех молекул остается постоянной, если не будет какого-либо внешнего вмешательства в
.
5 Молекулы не действуют друг на друга ни притягивающе, ни отталкивающе, кроме как в процессе столкновения. Между столкновениями они движутся прямолинейно. 9{\text{2}}\text{)}_{\text{ave}} \quad \label{1} \] Где P, V = давление и объем газа
N = количество молекул
m = масса каждой молекулы
( u 2 ) ave = среднее (или среднее) из квадратов всех индивидуальных молекулярных скоростей. Необходимо использовать эту среднеквадратичную скорость, потому что давление пропорционально квадрату скорости молекул, а столкновения молекул приводят к тому, что разные молекулы имеют совершенно разные скорости.
Вместо того, чтобы заниматься процедурой получения уравнения. \(\ref{1}\), давайте изучим уравнение и увидим, что его общие черты во многом соответствуют нашим ожиданиям. В некотором смысле возможность сделать это с помощью формулы более полезна, чем возможность ее вывести. Рисунок \(\PageIndex{1}\)
Во-первых, уравнение говорит нам, что давление газа пропорционально числу молекул, деленному на объем.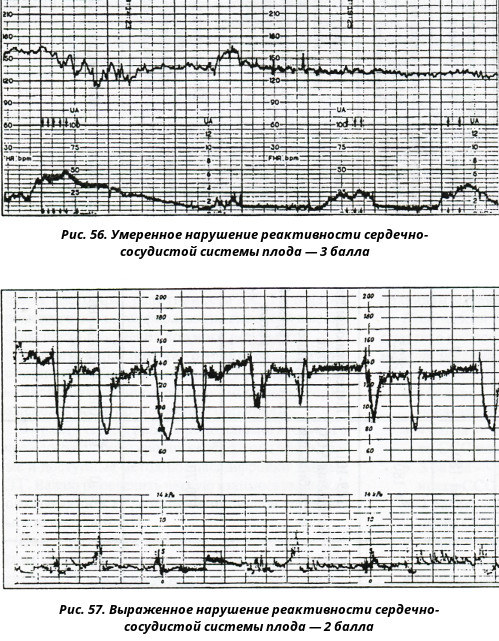 Это показано графически на рисунке \(\PageIndex{1}\), где компьютер нарисовал одинаковое количество молекул газа, занимающих каждый из трех разных объемов. «Хвост» каждой молекулы показывает точный путь, по которому эта молекула прошла за предыдущую микросекунду — чем длиннее хвост, тем быстрее двигалась молекула. Среднее квадратов длин хвостов пропорционально ( u 2 ) ave и одинакова на всех трех диаграммах. Также предполагается, что все молекулы имеют равные массы.
Это показано графически на рисунке \(\PageIndex{1}\), где компьютер нарисовал одинаковое количество молекул газа, занимающих каждый из трех разных объемов. «Хвост» каждой молекулы показывает точный путь, по которому эта молекула прошла за предыдущую микросекунду — чем длиннее хвост, тем быстрее двигалась молекула. Среднее квадратов длин хвостов пропорционально ( u 2 ) ave и одинакова на всех трех диаграммах. Также предполагается, что все молекулы имеют равные массы.
Как видите, уменьшение объема газа увеличивает количество столкновений на единицу площади со стенками контейнера. Каждое столкновение воздействует на стену; сила на единицу площади — это давление, поэтому количество столкновений на единицу площади пропорционально давлению. Уменьшение объема вдвое удваивает давление, предсказание, которое согласуется с экспериментальными фактами, обобщенными в законе Бойля. Уравнение \(\ref{1}\) также говорит о том, что давление пропорционально массе каждой молекулы газа. Опять же, это то, что мы ожидаем. Тяжелые молекулы дают больший «толчок» (технический термин для этого — импульс ) о стену, чем легкие с той же скоростью.
Опять же, это то, что мы ожидаем. Тяжелые молекулы дают больший «толчок» (технический термин для этого — импульс ) о стену, чем легкие с той же скоростью.
Наконец, уравнение говорит нам, что давление пропорционально среднему квадрату скоростей молекул. Эта зависимость от квадрата скорости разумна, если мы понимаем, что удвоение скорости молекулы имеет два эффекта.
Во-первых, молекула может двигаться дальше за заданный промежуток времени, удваивая количество столкновений со стенками. Это удвоит давление. Во-вторых, удвоение скорости молекулы удваивает толчок или импульс каждого столкновения. Это снова удваивает давление. Следовательно, удвоение скорости молекулы увеличивает давление в четыре раза, а для большого числа молекул P пропорционально средней квадратной скорости.
Эта страница под названием 9.13: Кинетическая теория газов — постулаты кинетической теории распространяется по лицензии CC BY-NC-SA 4. 0, ее авторами, ремиксами и/или кураторами являются Эд Витц, Джон У. Мур, Джастин Шорб. , Ксавьер Прат-Ресина, Тим Вендорф и Адам Хан.
0, ее авторами, ремиксами и/или кураторами являются Эд Витц, Джон У. Мур, Джастин Шорб. , Ксавьер Прат-Ресина, Тим Вендорф и Адам Хан.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ХимПРАЙМ
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет на странице
- Теги
- импульс
- кинетическая молекулярная теория
- кинетическая теория
- КТ
- Постулаты кинетической теории
Средняя длина свободного пробега и частота столкновений (производное)
Средняя длина свободного пробега — это среднее расстояние, которое частица проходит без столкновения с другими частицами!
youtube.com/embed/56JxrWySbvg?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>- 1 Введение
- 2 Расчет среднего свободного пути
- 3 Расчет частоты столкновения
- 4 Вывод фактора 1/√2
- 4.1 Концепция модели
- 4.2.
- 4.3 Заключение
Введение
В статье Распределение Максвелла-Больцмана показано, что средняя скорость ( средняя скорость ) частиц идеального газа может быть определена по следующей формуле:
\begin{align}
\label{v}
&\boxed{ \bar{v} = \sqrt{\frac{8 k_B T}{\pi m}} } \\[5px]
\end{ align}
Эту формулу можно использовать, например, для оценки средней скорости частиц воздуха. Поскольку 78 % воздуха состоит из азота, необходимо рассчитать среднюю скорость молекул азота (N 2 ). Такая частица азота имеет массу 4,65 ⋅ 10 -26 кг.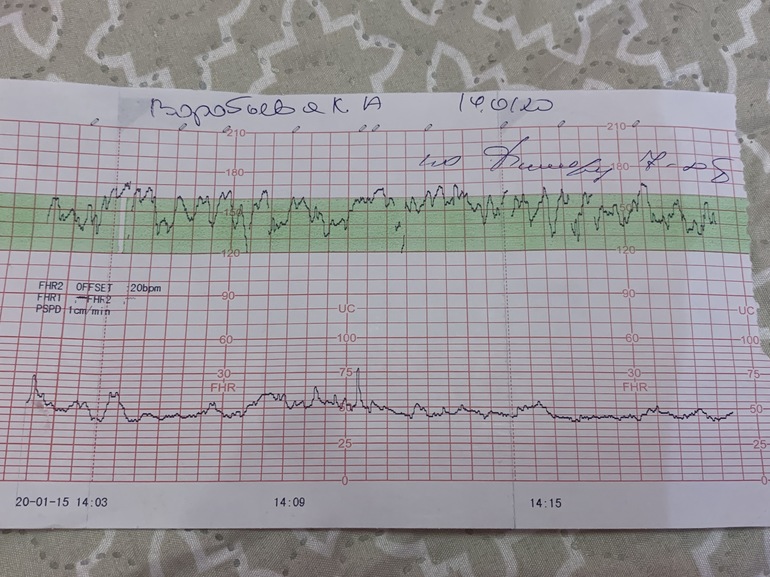 При температуре 20° C (293 K) это дает среднюю скорость около 470 м/с.
При температуре 20° C (293 K) это дает среднюю скорость около 470 м/с.
В среднем частицы воздуха движутся со сверхзвуковой скоростью. Однако из-за статистического распределения скоростей также присутствуют значительно более высокие скорости. Около 1 % молекул имеют скорость более 1000 м/с. Одна молекула из миллиарда даже достигает скорости 2000 м/с.
Если молекулы газа вообще имеют такие большие скорости, почему бы сразу не почувствовать запах открытого парфюмерного флакона в другом конце комнаты, как и следовало ожидать при скоростях в несколько сотен метров в секунду. Опыт показывает, что для того, чтобы аромат стал заметен, требуется некоторое время.
Рис.: Схематическое изображение распределения ароматических молекул в воздухе Кажущееся противоречие заключается в том, что частицы газа не имеют свободного пробега при движении. Молекулы будут постоянно сталкиваться с другими частицами и случайным образом менять направление своего движения. Расстояние, которое молекула может пройти в среднем без столкновения с другими молекулами, называется средней длиной свободного пробега . В данном случае относительно малая длина свободного пробега частиц ароматизатора препятствует мгновенному восприятию аромата.
В данном случае относительно малая длина свободного пробега частиц ароматизатора препятствует мгновенному восприятию аромата.
Длина свободного пробега — это среднее расстояние, которое частица проходит без столкновения с другими частицами!
Тот факт, что аромат, тем не менее, воспринимается относительно быстро, в основном обусловлен воздушными потоками (конвекциями), которые переносят частицы на большие расстояния. Обратите внимание, что конвекция больше не является полностью случайным движением. В этом случае молекулы перемещаются на макроскопические расстояния в определенном направлении.
Расчет длины свободного пробега
Для определения длины свободного пробега частицы рассматривается газ, состоящий только из молекул одного типа. Молекулы предполагаются сферами диаметром d. Если теперь следовать за частицей (показана красным на рисунке ниже), она будет сталкиваться с другими частицами через неравные промежутки времени (показаны черным).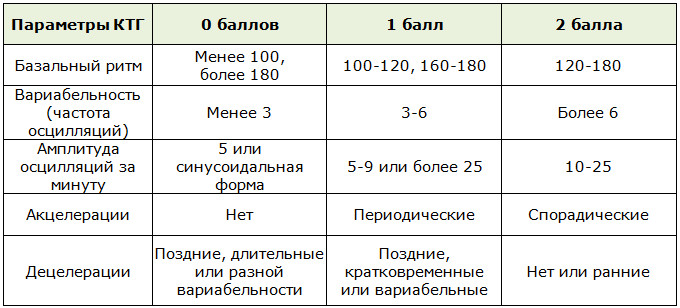 Среднее расстояние, пройденное между двумя последовательными столкновениями, соответствует средней длине свободного пробега λ.
Среднее расстояние, пройденное между двумя последовательными столкновениями, соответствует средней длине свободного пробега λ.
Ради простоты все частицы (за исключением частицы, за которой следует мысль) считаются полностью покоящимися. Отслеживаемая таким образом частица движется через «океан» покоящихся частиц и меняет направление после каждого свободного пути.
Анимация: средний свободный пробег (неподвижные частицы) Столкновение между движущейся частицей и неподвижной частицей произойдет, когда поверхности сферических частиц соприкоснутся друг с другом. Это будет иметь место, если расстояние между центрами тяжести меньше удвоенного радиуса частицы. 92 ~~~~~\text{сечение столкновения} \\[5px]
\end{align}
В направлении движения получится воображаемый цилиндр столкновения ( объем столкновения ). Если центр тяжести частицы находится внутри этого цилиндра, произойдет столкновение. Длина цилиндра столкновения соответствует длине свободного пробега λ.
Длина цилиндра столкновения соответствует длине свободного пробега λ.
(Средний) объем цилиндра столкновения V c является результатом произведения сечения столкновения 92 \cdot \lambda~~~~~\text{цилиндр столкновения} \\[5px]
\end{align}
В каждом цилиндрическом объеме столкновения V c =σ⋅λ по определению есть только одна частица, а именно частица, с которой сталкивается движущаяся частица. Затем движущаяся частица изменит свое направление и определит новый объем столкновения, опять же с «целевой» частицей, с которой она столкнется.
Утверждение, что внутри цилиндра столкновения находится только одна единственная молекула, в конечном счете относится к центру тяжести частиц. В общем, будет несколько частиц, поверхность которых достигнет объема столкновения, но только если центр тяжести находится внутри этого цилиндра, действительно произойдет столкновение. Это будет иметь место только для одной молекулы, потому что с этого момента будет определяться новый объем столкновения, пока, наконец, не произойдет новое столкновение. Это рассмотрение центра тяжести также имеет смысл, поскольку частицы все еще можно представить в виде материальных точек, окруженных сферической «оболочкой столкновения». При таком допущении в виде массовых точек становится ясно, что на самом деле в столкновительном объеме находится только одна частица (см. рисунок ниже).
Это рассмотрение центра тяжести также имеет смысл, поскольку частицы все еще можно представить в виде материальных точек, окруженных сферической «оболочкой столкновения». При таком допущении в виде массовых точек становится ясно, что на самом деле в столкновительном объеме находится только одна частица (см. рисунок ниже).
Количество молекул в определенном объеме также можно определить по плотности частиц n в газе. Эта плотность частиц n вычисляется как частное общего числа частиц N и всего объема газа V:
\begin{align}
& n = \frac{N}{V} ~~~~~\ text{плотность частиц}\\[5px]
\end{align}
Плотность частиц указывает количество частиц в единице объема. Если умножить эту плотность частиц n на любой объем V 92}}
\end{align}
Длина свободного пробега зависит только от плотности частиц и их диаметра! Однако это соображение основывалось на стационарных частицах. Однако на самом деле отдельные молекулы будут двигаться относительно друг друга.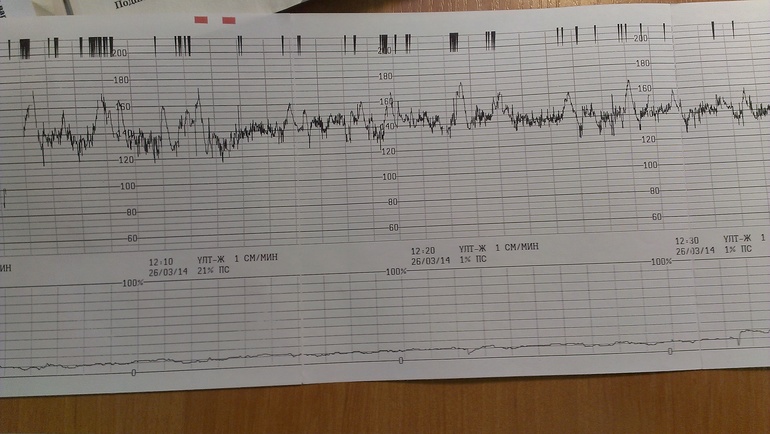 Предполагается, что это приведет к увеличению количества столкновений за раз и, следовательно, уменьшит длину свободного пробега. Принимая во внимание распределение скоростей Максвелла-Больцмана, длина свободного пробега укорачивается в 1/√2 раз (вывод этого коэффициента показан в последнем разделе): 92}} ~~~~~\text{}n=\frac{N}{V}
Предполагается, что это приведет к увеличению количества столкновений за раз и, следовательно, уменьшит длину свободного пробега. Принимая во внимание распределение скоростей Максвелла-Больцмана, длина свободного пробега укорачивается в 1/√2 раз (вывод этого коэффициента показан в последнем разделе): 92}} ~~~~~\text{}n=\frac{N}{V}
\end{align}
Для идеального газа плотность частиц n=N/V также может быть выражено термодинамической температурой T и давлением p в соответствии с законом идеального газа:
\begin{align}
&pV=N k_B T ~~~~~\text{закон идеального газа}\\[5px]
\ label{n}
&n=\frac{N}{V}=\frac{p}{k_B T}\\[5px]
\end{align}
Если уравнение (\ref{n}) используется в уравнения (\ref{l}), то длину длины свободного пробега также можно определить следующим образом: 92}}
\end{align}
Если молекула азота диаметром около d = 370 пм (это соответствует сечению столкновения σ = 4,3·10 -19 м²) и температуре T= 293 K и давление p = 1 бар, средняя длина свободного пробега λ = 67 нм. При этом длина свободного пробега примерно в 10 раз меньше длины волны видимого света!
При этом длина свободного пробега примерно в 10 раз меньше длины волны видимого света!
Расчет частоты столкновений
Если помимо длины (среднего) свободного пробега λ известна также (средняя) скорость \(\overline{v}\) молекул, то (средняя) ) можно определить период времени τ между двумя столкновениями:
\begin{align}
& \text{скорость} \overline{v}= \frac{\text{расстояние}\lambda}{\text{время} \tau} \\[5px]
\label{t }
& \boxed{\tau = \frac{\lambda}{\overline{v}}} ~~~~~\text{длительность между двумя столкновениями}
\end{align}
Это среднее время между двумя столкновениями имеет смысл периода τ, так как указывает повторяющиеся интервалы времени, в течение которых в среднем происходят столкновения. Следовательно, обратную величину времени τ можно понимать как частоту столкновений f, который указывает количество столкновений в единицу времени. Эта частота столкновений часто обозначается буквой Z.
\begin{align}
& Z = f = \frac{1}{\tau} \\[5px]
\label{zz}
& \boxed{Z = \frac{\overline{v}}{\lambda}} ~~~~~\text{частота столкновений}
\end{align}
Количество столкновений в единицу времени между частицей и ее «целевыми» частицами называется частотой столкновений!
Если в формуле для частоты столкновений используются уравнение (\ref{v}) для средней скорости и уравнение (\ref{lam}) для длины свободного пробега, получается следующая формула: 94}{k_B T m}} } \\[5px]
\end{align}
Для уже рассмотренной молекулы азота при температуре 293 К и давлении 1 бар частота столкновений 7·10 9 1/с результатов, то есть в течение одной секунды одна молекула азота столкнется в среднем с 7 миллиардами других молекул!
Чтобы получить общее количество столкновений на единицу объема и времени, нужно всего лишь умножить частоту столкновений Z на плотность частиц n («количество частиц на единицу объема»).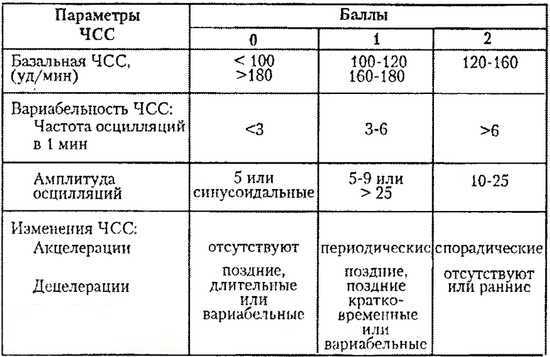 Следует отметить, что каждая частица будет сталкиваться по две, так что коэффициент ½ все же необходимо учитывать. Если плотность частиц n выразить через температуру и давление по уравнению (\ref{n}), то общее число столкновений в единицу объема и времени определяется следующим образом: 93 м}} } ~~~~~\text{общее количество столкновений на единицу объема и времени}
Следует отметить, что каждая частица будет сталкиваться по две, так что коэффициент ½ все же необходимо учитывать. Если плотность частиц n выразить через температуру и давление по уравнению (\ref{n}), то общее число столкновений в единицу объема и времени определяется следующим образом: 93 м}} } ~~~~~\text{общее количество столкновений на единицу объема и времени}
\end{align}
Для азота общее число z = 8,7·10 34 1/см³ равно получается, т.е. за одну секунду в объеме одного кубического метра происходит 8,7·10 34 столкновений (чертовски много столкновений в секунду!).
Вывод коэффициента 1/√2
В этом разделе необходимо прояснить вопрос, как именно возникает коэффициент 1/√2 в уравнении (\ref{lam}) для длины свободного пробега. Исходной ситуацией было предположение, что все «целевые» молекулы движущейся молекулы покоятся.
Концепция модели
По аналогии можно представить рынок с большим количеством людей, который хотелось бы пройти пешком. Тем не менее, все люди пока остаются в покое. Теперь человек начинает идти прямо. Каждый раз, встречая человека, он случайным образом меняет направление, а затем снова идет прямо. Расстояние, которое можно пройти в среднем, не сталкиваясь с человеком, в переносном смысле соответствует среднему свободному пробегу .
Тем не менее, все люди пока остаются в покое. Теперь человек начинает идти прямо. Каждый раз, встречая человека, он случайным образом меняет направление, а затем снова идет прямо. Расстояние, которое можно пройти в среднем, не сталкиваясь с человеком, в переносном смысле соответствует среднему свободному пробегу .
Свободный путь на рынке можно определить следующим образом. Для этого нужно измерить время между двумя столкновениями и, с другой стороны, нужна скорость, с которой человек движется. Из произведения (среднего) времени τ 0 и (средняя) скорость \(\overline{v}\) результаты (среднего) свободного пробега λ:
\begin{align}
& \lambda_0 = \overline{v} \cdot \tau_0 ~~~ ~~\text{среднее значение свободного пути для стационарных «целей»}
\end{align}
Теперь предположим, что люди на рынке движутся хаотично, когда кто-то его пересекает. Продолжительность τ между двумя столкновениями снова может быть определена простым измерением. Хотя человек по-прежнему идет по рынку с той же скоростью, он заметит, что среднее время между двумя столкновениями сократилось (τ<τ 0 ). Это также сокращает средний свободный пробег (λ<λ 0 ):
Хотя человек по-прежнему идет по рынку с той же скоростью, он заметит, что среднее время между двумя столкновениями сократилось (τ<τ 0 ). Это также сокращает средний свободный пробег (λ<λ 0 ):
\begin{align}
& \lambda = \overline{v} \cdot \tau ~~~~~\text{средний свободный путь для перемещения «цели»}
\end{align}
Сокращение времени (или длины свободного пробега) в конечном счете связано с тем, что не только собственная скорость определяет интервал времени между двумя столкновениями, но и относительная скорость с который движется к цели. Таким образом, скорость окружающих людей также имеет значение. Относительная скорость в основном также имеет решающее значение в случае стационарных «целей», но поскольку они считаются стационарными, относительная скорость соответствует скорости, с которой человек движется!
Перенос концепции модели на газы
Если эта концепция модели переносится на газ, то среднюю скорость \(\overline{v}\) частицы нельзя использовать в качестве основы для среднего времени между двумя столкновениями , а скорее означает относительную скорость \(\overline{v_{rel}}\), с которой частицы в среднем приближаются друг к другу.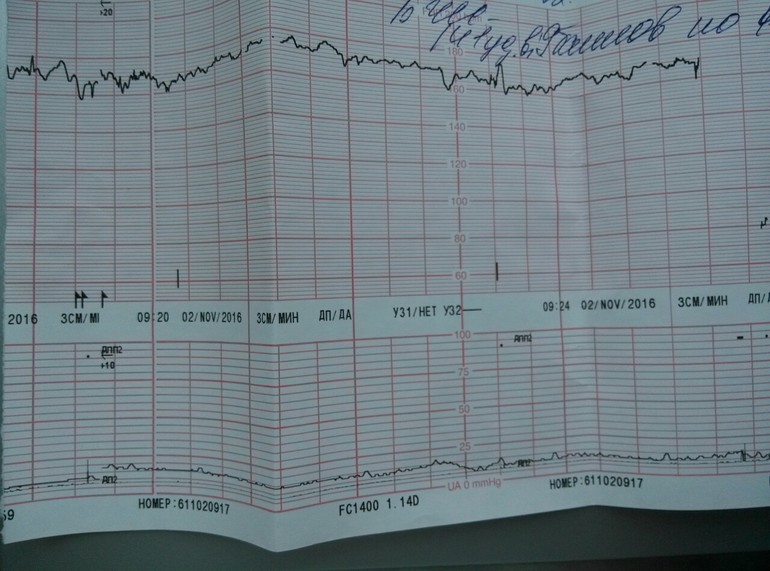 Из статистических соображений можно вывести зависимость между этими двумя скоростями.
Из статистических соображений можно вывести зависимость между этими двумя скоростями.
Для этого рассматриваются две частицы, которые будут сближаться и сталкиваться друг с другом. Векторы скоростей двух частиц можно расположить как угодно (см. рисунок ниже). С точки зрения частицы 1 относительная скорость, с которой движется частица 2, получается из разности векторов скоростей:
\begin{align}
\label{rel1}
& \vec{v_{rel}} = \vec{v_2} – \vec{v_1} \\[5px]
\end{align}
Так как позднее для (среднего) свободного пробега имеет значение только модуль (среднего) вектора относительной скорости, в этой точке не имело бы значения, в каком порядке векторы скорости вычитались бы из каждого Другой. Можно было бы поменять местами индексы в приведенном выше уравнении. Таким образом можно было бы описать сближение частиц с точки зрения частицы 2. 92\\[5px]
\end{align}
Примечание : Для ясности величина скорости обозначается только символом v без каких-либо дополнительных указаний. Если же имеется в виду вектор скорости \(\vec{v}\), то над символом явно ставится стрелка.
Если же имеется в виду вектор скорости \(\vec{v}\), то над символом явно ставится стрелка.
Величина относительной скорости v rel (относительная скорость) может быть выражена следующим образом через соответствующий вектор \(\vec{v_{rel}}\):
\begin{align}
\label{ отн2} 92}} _ {\ text {термин 2}} —
\ underbrace {\ overline {2 \ vec {v_1} \ vec {v_2}}} _ {\ text {термин 3}} \\ [5px]
\ end {align}
Первый член, который содержит квадрат скорости частицы 2, в среднем не отличается от второго члена, который содержит квадрат скорости частицы 1. Из-за случайных движений средняя скорость двух частиц – или, вернее, все частицы – идентичны. Уже упоминалось, что индексы могли быть заменены местами. Вопрос только в том, наблюдается ли столкновение с одной частицы или с другой. Средние скорости v 92} \\[5px]
\end{align}
Третий член уравнения (\ref{term}) содержит скалярное произведение векторов скорости. Как обычно со скалярным произведением, отдельные компоненты скорости умножаются друг на друга, а затем суммируются.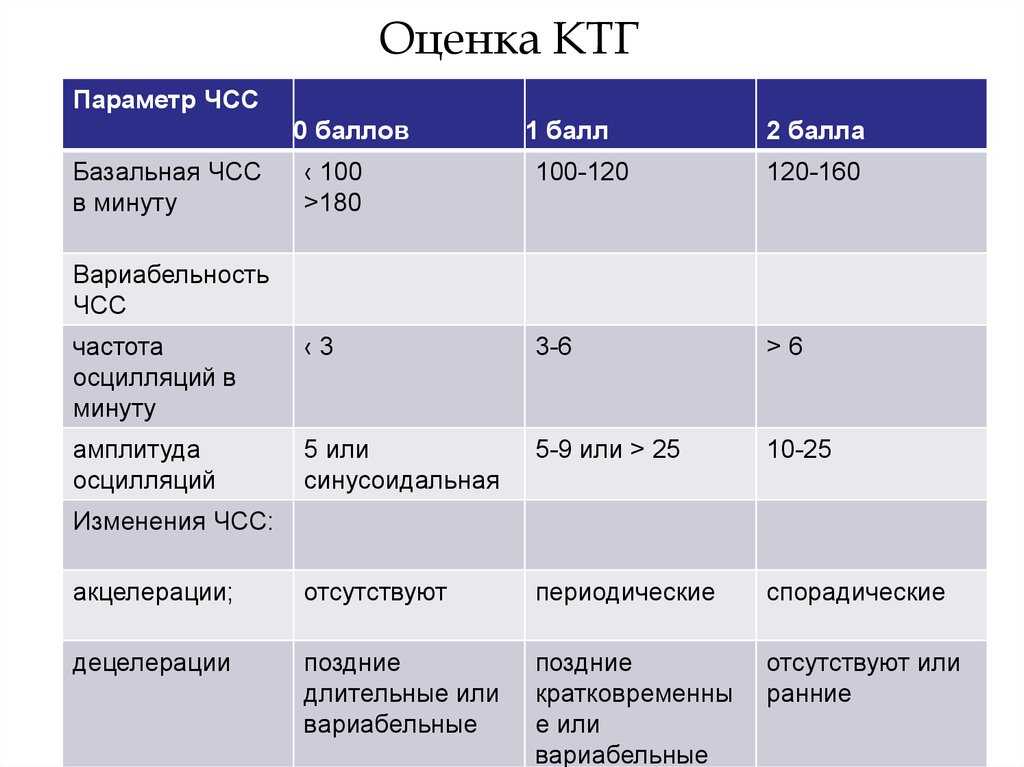

 По своей сути оно представляет собой постоянную, непрерывную регистрацию сердечных сокращений малыша, маточных сокращений, а также двигательной активности ребенка. Все эти параметры фиксируются синхронно и сразу в режиме реального времени записываются самописцем или компьютерной программой на калибровочную ленту.
По своей сути оно представляет собой постоянную, непрерывную регистрацию сердечных сокращений малыша, маточных сокращений, а также двигательной активности ребенка. Все эти параметры фиксируются синхронно и сразу в режиме реального времени записываются самописцем или компьютерной программой на калибровочную ленту.