Математика — это красиво! Графическая тетрадь №2 — Лучшие Детские Книги
Где купить: Лабиринт / Бук 24 / Озон / Майшоп
Название: Математика — это красиво! Графическая тетрадь №2
Автор: Вельтман Анна
ISBN: 978-5-00117-588-9
Издательство: Манн, Иванов и Фербер
Год выпуска: 2018
Описание:
О книге
Это продолжение первой графической тетради «Математика — это красиво». Она покажет, что скучный на первый взгляд предмет может быть искусством, основанным на числах.
На страницах этой графической тетради с помощью законов математики и простых инструментов — карандаша, линейки, циркуля и ножниц — вы сможете рисовать цепочки, безумные кривые, числовые спирали, узлы, переплетения и круговые узоры, искривлять картинки, рассчитывать траекторию движения бильярдного шара и многое другое. А ещё — удивлять всех геометрическими фокусами. Ну и замостить котами кубик, что тоже немаловажно.
Не имеет значения, любит ли ваш ребенок считать или рисовать, в этой тетради он познакомится с разными математическими понятиями и сможет на практике увидеть связь между математикой и изобразительным искусством.
Фишки книги
Продолжение полюбившейся тетради;
Развивает аналитическое и творческое мышление;
Доказывает, что математика — это искусство;
Легко и в игровой форме рассказывает о сложных математических понятиях;
Пригодится любому школьнику;
Первая тетрадь получила награды в престижном конкурсе British book design and Production awards и «Книга года 2015: выбирают дети».
Для кого эта книга
Для всех детей от 8 лет 12 лет.
Для родителей и учителей, которые хотят увлечь детей математикой
Об авторе
Анна Вельтман — школьный учитель из Нью-Йорка, США. Испытывая истинную любовь к математике, Анна старается донести до детей, что эта наука является основой всего, что нас окружает, в том числе музыки и изобразительного искусства. В свободное от занятий математикой время Анна посвящает себя живописи, прикладному искусству, кулинарии и написанию музыки.
Математика — это красиво! Графическая тетрадь
О книге
Эта необычная тетрадь покажет вам, что математика может быть красивой, а гармония в изобразительном искусстве основана на числах.
На страницах этой графической тетради, с помощью законов математики и простых инструментов — карандаша, линейки и циркуля, — вы сможете создавать удивительные фигуры: идеальные окружности и гексагоны, золотую спираль и треугольник Серпинского, трёхмерные рисунки и необычные мозаики. Вы увидите, как числа превращаются в змейки и разноцветные узоры, линии — в звёзды и паутину, а геометрические фигуры — в снежинки, животных и растения.
Неважно, любит ли ваш ребенок считать, чертить или рисовать, в этой тетради, он познакомится с самыми разными математическими понятиями и концепциями и сможет увидеть связь между математикой и искусством.
Фишки книги
В конце книги вы найдете чистые, разлинованные листы, на которых сможете придумать собственные математико-художественные шедевры.
Почему мы решили издать эту книгу
Эта тетрадь с, казалось бы, простыми заданиями открывают ребенку удивительный и гармоничный мир изобразительного искусства, построенного на математике, — мир, где живут геометрические фигуры, удивительные кривые, необычные узоры и симметрия.
| Характеристики | |
| Автор | Вельтман Анна |
| Художник | Черно-белые, Цветные |
| Переводчик | Филин Сергей |
| Год издания | |
| Тип бумаги | офсет |
| Страниц | 90 |
| Вес | 484 |
| Размеры | 282x220x10 |
| Издательство | Манн, Иванов и Фербер |
| EAN | 9785000574317 |
| Возраст | Детям от 6 до 12 лет |
Анна Вельтман.
Математика — это красиво Когда увидела впервые эту книгу — графическую тетрадь — на сайте издательства +Манн, Иванов и Фербер, то решила, что она для старших дошкольников и младших школьников. Достаточно плотные страницы, на которых можно рисовать карандашами или фломастерами, гибкий переплёт, позволяющий вполне комфортно работать с книгой, развернув её, яркие иллюстрации, доступный язык — казалось, что книга именно для тех, кто только делает первые шаги в математике. Принесла на работу и показала нескольким учителям математики. Оказалось, что я неправа. Одна коллега тут же заказала себе эту книгу для внеурочной работы по математике с пятиклассниками, сопроводив своё желание словами о том, что в контексте ФГОС эта графическая тетрадь — настоящая находка (вряд ли автор — школьный учитель из Нью-Йорка — в курсе наших требований к результатам, но вот оно как оказалось). Другая, полистав, сказала, что задания книги рассчитаны на разный возраст — с ней можно работать, начиная с начальной школы и вплоть до 8 класса.
Когда я училась в школе, помню, что геометрию мы любили больше, чем алгебру. А потому меня удивляет то, что нынешние школьники (смотрю по своей дочери-восьмикласснице, её друзьям, а также разговорам старшеклассников на переменах), про клиповое мышление которых не написал только ленивый, с геометрией не особенно дружат. Казалось бы, именно визуализация должна выигрывать у формализации, но в действительности получается наоборот. Говорила об этом с коллегами-математиками — подтверждают, но не объясняют причин. Подумала: может быть, прагматичность современных подростков требует практического применения изучаемого материала (к слову, к другим предметам школьной программы это тоже относится)?
Книга-тетрадь учит построениям самых разных фигур с помощью линейки и циркуля: от обычных треугольников до трёхмерных изображений на бумаге. Молодой учитель математики нашей гимназии +Рената Шафикова воспользовалась идеями книги, связанными с построениями окружности. Именно эта тема изучается в 6 классе, а потому шестиклассники с удовольствием рисовали с помощью циркуля мандалы, а потом раскрашивали их. Обычные окружности сплетались в причудливые узоры.Или такие.
Такие похожие, но такие разные! Больше примеров можно посмотреть в альбоме.А вот, взглянув, на этот рисунок, учитель математики поймёт, над чем ещё надо поработать при построении окружностей. Правда?
Когда на перемене шестиклассники сдавали свои работы учителю, в кабинет зашёл восьмой класс. Сама была свидетелем, как несколько человек, увидев рисунки, с надеждой спросили: «А мы? Мы будем так рисовать на математике?». Кому-то такая работа может показаться забавами и ребячеством, однако, в этой графической тетради найдутся и задания, посвящённые параболам (7 класс), и правильным гексогенам, шестиугольникам (8 класс).
Книга открывается такими словами:
Как вы думаете, о ком я вспомнила, едва прочитав эту страницу? Правильно, о +Ljudmilla Rozhdestvenskaja! Хоть я и не математик, но каждый раз зачитываюсь её публикациями, посвящённым рисованию математическими методами картин художников-авангардистов. Кстати, о мандалах она тоже писала. Чем не идея для продолжения работы с шестиклассниками? Сначала нарисовали на бумаге, а затем — в GeoGebra — с постепенным усложнением задания.И это можно делать не только с мандалами. Вот, к примеру, фрагмент одного из разворотов графической тетради.
А вот здесь — публикация Людмилы об идеях ученических проектов на эту тему. Чувствуете, как можно, начав с элементарных заданий, заинтересовать школьников и вывести их на более сложный уровень?
В книге есть развороты, посвящённые снежинке Коха и треугольнику Серпинского.
У Людмилы есть публикация и на эту тему.
В конце книги приводятся идеи для дальнейшей работы, а также словарь основных терминов (признаюсь, некоторые слова оказались для меня незнакомыми).
Всё-таки каким увлекательным может быть изучение математики!
|
|
72 МБ
64 МБ
20 МБ
74 МБ
И только сегодня к читателю возвращается книга в своем первоначальном виде. Для среднего школьного возраста.
На страницах этой графической тетради, с помощью законов математики и простых инструментов — карандаша, линейки и циркуля, — вы сможете создавать удивительные фигуры: идеальные окружности и гексагоны, золотую спираль и треугольник Серпинского, трёхмерные рисунки и необычные мозаики. Вы увидите, как числа превращаются в змейки и разноцветные узоры, линии — в звёзды и паутину, а геометрические фигуры — в снежинки, животных и растения. Неважно, любит ли ваш ребенок считать, чертить или рисовать, в этой тетради, он познакомится с самыми разными математическими понятиями и концепциями и сможет увидеть связь между математикой и искусством. В конце книги вы найдете чистые, разлинованные листы, на которых сможете придумать собственные математико-художественные шедевры. Эта тетрадь с, казалось бы, простыми заданиями открывают ребенку удивительный и гармоничный мир изобразительного искусства, построенного на математике, — мир, где живут геометрические фигуры, удивительные кривые, необычные узоры и симметрия.
Для детей 8-12 лет. Для родителей и учителей, которые хотят увлечь детей математикой.
Будущие первоклассники смогут повторить счет, решить простые примеры и нелегкие логические задачи, научатся уравнивать количество предметов и закрепят понятия «больше — меньше». Выполнять задания будет нескучно — все они даны в игровой, занимательной форме. Кроме того, дети узнают немало интересных фактов из жизни животных, порисуют, разгадают кроссворды. Полезное и увлекательное занятие для детей — графические диктанты. Это эффективная подготовка к урокам математики. Также они полезны для развития пространственного мышления, воображения, памяти, мелкой моторики рук. Советуем сначала взрослому диктовать маленькому ученику последовательность действий с указанием числа клеточек и их направлений, контролируя каждое его действие. При систематических занятиях графическими диктантами ребёнок научится умело решать даже самые сложные задания.»
Учебное пособие
Просто берешь кубики и собираешь сложную программу или игру. Давай вместе отправимся в удивительный мир программирования.
Знакомясь с первыми главами, написанными простым и понятным для детей языком, начать осваивать персональный компьютер могут не только учащиеся начальных классов, но и дошкольники. В первой и второй главах даны основополагающие сведения о компьютере и его составных частях, о программном обеспечении и системе управления компьютером, а также об организации хранения информации и о правилах работы с файлами и папками. 15 отдельных главах в простой и доступной форме изложены особенности работы с программами, наиболее часто используемыми школьниками при выполнении различных учебных задач, например с графическим редактором Paint, с текстовым редактором Word, а также с приложением PowerPoint. Соответствующие главы посвящены рассмотрению особенностей использования ресурсов сети Интернет при изучении предметов школьной программы. Особое внимание уделено вопросам безопасности при работе и общении детей в сети Интернет. Прежде чем разрешить ребенку начать осваивать персональный компьютер с помощью этой книги, авторы настоятельно рекомендуют родителям внимательно ознакомиться с главой «Советы родителям», которая предназначена специально для них.
Все главы и разделы сопровождаются поясняющими рисунками, благодаря которым восприятие и усвоение ребенком изложенной информации происходят значительно быстрее и эффективнее, чем при чтении скучного учебника.
Антокольской открывает знаменитую математическую трилогию В. Лёвшина «Магистр Рассеянных Наук». Герой этой повести, как можно догадаться, — Магистр. Магистр, написавший книгу о своих приключениях. Каждая её глава полна всевозможных математических несуразиц и ошибок, которые нужно обязательно исправить. К решению этой непростой задачи и подключается Клуб Рассеянного Магистра — школьники Таня, Сева и Олег, знакомые нам по книгам «Три дня в Карликании» и «Чёрная маска из Аль-Джебры». Вместе с ними и читателю предстоит поучиться на ошибках рассеянного математика и познакомиться с правилами и парадоксами самой точной в мире науки.»
00 МБ
40 МБ
81 МБ
88 МБ10 лучших математических приложений для школьников – TeenLife
Домашнее задание по математике заставляет вас дрожать? Это сделало меня.
К сожалению, у нас не было такой широкой доступности приложений, которая есть у сегодняшних студентов. Математические приложения добавляют совершенно новое измерение к обучению и дают вам возможность иметь эти вспомогательные средства прямо у вас под рукой.
Вот 10 математических приложений, которые вы можете загрузить, чтобы помочь с этими вездесущими математическими вопросами:
1. Бесплатный графический калькулятор (iOS) / Графический калькулятор от MathLab (Android)
Раньше графические калькуляторы были дорогими, сложными и довольно забавными, если на них можно было программировать игры.Однако те, кто изучает высшую математику, могут загрузить эти приложения. Эти бесплатные приложения предоставляют пользователям расширенные операции, функции, интуитивно понятный пользовательский интерфейс и красиво оформленные графики с уклонами, корнями и пересечениями — и это лишь некоторые из них.
2. Преобразование единиц бесплатно (iOS) / Конвертер единиц (Android)
Эти приложения позволяют конвертировать практически все, будь то валюта, данные, энергия, мощность или температура.
Путешественники по всему миру также могут конвертировать валюту в режиме реального времени, используя актуальные обменные курсы.Эти бесплатные приложения позволяют быстро и легко создавать собственные преобразования единиц для чего угодно.
3. MathRef (iOS)
MathRef — надежное приложение для быстрого поиска формул в различных дисциплинах. Это приложение не охватывает столько дисциплин, как Wolfram Alpha, но, возможно, в этом его сила, поскольку оно больше ориентировано на традиционные математические области, такие как алгебра, геометрия и исчисление. MathRef также имеет отличный пользовательский интерфейс, позволяющий пользователям добавлять примечания к уравнениям, сохранять избранные уравнения и копировать текст из приложения в сообщения электронной почты или текстовый редактор.
4. Wolfram Alpha (Android, iOS)
Wolfram Alpha предлагает подробные ответы на любые вопросы, связанные с математикой или числами, которые у вас могут возникнуть.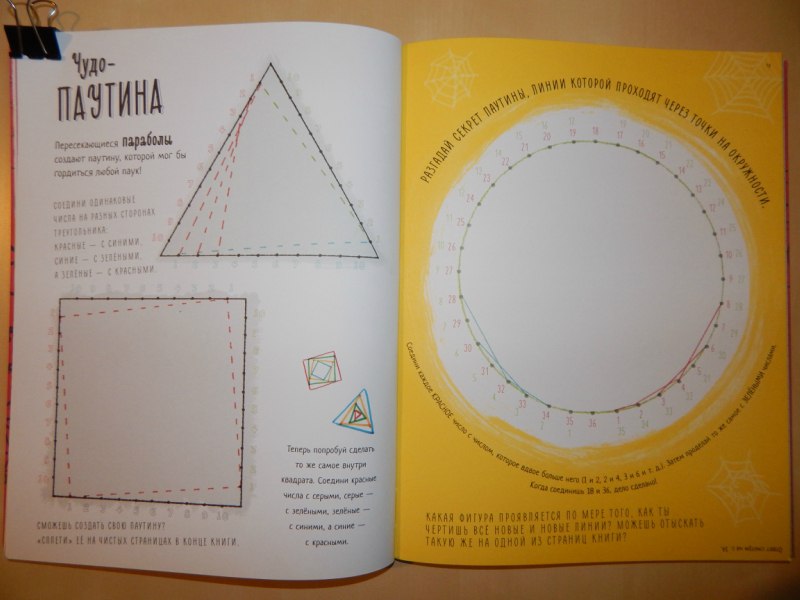
Этот вычислительный двигатель знаний может вычислять почти все в 29 дисциплинах. Вы можете получить подробные сведения о формулах, графические изображения и краткие пояснения, которые помогут вам понять, как приложение пришло к данному решению.
5. Цифры (iOS)
После выполнения стандартных расчетов Digits сохраняет вашу работу на экранной ленте, похожей на старые бухгалтерские калькуляторы с бумажной лентой.Если вы допустили ошибку где-либо на ленте, «проверьте ленту», чтобы найти ошибку и исправить расчет на месте. После того, как вы сделали все необходимые расчеты, вы можете сохранить и поделиться своей лентой для печати или дальнейших манипуляций в Apple Numbers или Microsoft Excel.
6. Мой калькулятор сценариев (iOS, Android)
Это приложение считывает ваш почерк, когда вы пишете на экране, что делает функциональность MyScript Calculator впечатляющей. Написав уравнение, которое вы хотите решить, на экране телефона или планшета, приложение расшифрует ваш текст, преобразует его в цифровой текст, а затем решит проблему за вас.
Так что, если вы не хотите искать конкретного оператора на клавиатуре своего телефона, это приложение для вас.
7. Математический решатель (Android)
Math Solver помогает решать математические уравнения. Он показывает вам ответ на проблему, а также шаги, используемые в решении. Приложение решает линейные уравнения и квадратные уравнения. Math Solver также упрощает выражения, решает буквальные и радикальные уравнения, коэффициенты и графические уравнения.
8. MathPage (iOS)
Хватит бороться со сложными, запутанными математическими понятиями.Если вы не можете решить задачу, TheMathPage покажет вам, как это сделать, с четкими пояснениями, простыми примерами и интерактивными вопросами (просто нажмите, чтобы открыть ответы). Это как иметь личного репетитора.
9. Уравнения All-in-One (iOS)
Equations All-In-One решает более 130 наиболее распространенных математических, химических и физических формул, используемых в университетах и средних школах по всему миру.
Каждая формула позволяет решить для любой переменной в данном уравнении. Это приложение необходимо любому студенту, но идеально подходит для занятий по математике, физике или химии.Он включает в себя конвертер единиц с возможностью преобразования всех основных единиц для физики и химии.
10. iMathematics Pro (iOS, Android)
С более чем 120 темами, более 1000 формул, привлекательным интерфейсом и 7 решателями и калькуляторами, это полный пакет для изучения математики.
Это лишь десять приложений, которые помогут вам с математическими приложениями. Вы можете искать дальше в iTunes или Google Play для сотен других.
Графические математические уравнения с помощником по математике Ink в OneNote для Windows 10
Прошлым летом мы представили помощника по математике Ink в OneNote — цифровой репетитор, который дает вам пошаговые инструкции о том, как решать математические задачи, написанные от руки.Сегодня мы рады сообщить, что помощник по математике Ink может рисовать графики ваших уравнений в OneNote для Windows 10.
Теперь, когда вы пишете свои математические уравнения, математический помощник Ink быстро строит интерактивный график, чтобы помочь вам визуализировать эти сложные математические понятия. Вы можете увеличивать масштаб и перемещать график, чтобы увидеть точки пересечения, или изменить значения параметров в уравнениях, чтобы лучше понять, как каждый из них отражается на графике. Наконец, вы можете сохранить скриншот графика прямо на своей странице, чтобы вернуться к нему позже.
Пять шагов для построения графика уравнения в OneNote
- Начните с написания уравнения. Например: y=x+3 или y=sin(x)+cos(2x) .
- Затем с помощью инструмента «Лассо» выберите уравнение, а затем на вкладке «Рисование» нажмите кнопку Math .
- В раскрывающемся меню на панели Math выберите вариант Graph in 2D . Вы можете играть с интерактивным графиком вашего уравнения: используйте один палец, чтобы переместить положение графика, или два пальца, чтобы изменить масштаб уровень.
- Используйте кнопки + и – , чтобы изменить значения параметров в вашем уравнении.
- Наконец, нажмите кнопку Вставить на страницу , чтобы добавить скриншот графика на свою страницу.
Доступность: Помощник по математике Ink доступен в OneNote для Windows 10 для подписчиков Office 365.
Как всегда, мы будем рады услышать ваши отзывы, поэтому, пожалуйста, оставляйте комментарии ниже или предлагайте и голосуйте за будущие идеи на странице OneNote UserVoice.
Для получения дополнительной информации посетите нашу страницу поддержки.
— Мина Спасич, руководитель программы математической группы
.11 Математические приложения и онлайн-инструменты, рекомендуемые учителями для PreK-12
Для некоторых учителей математики цифровые инструменты, которые помогают учащимся визуализировать математические концепции, такие как Desmos, или веб-сайты, поощряющие математические дискуссии, такие как Fraction Talks, уже были частью их репертуара до пандемии.
Но других учителей дистанционное обучение впервые подтолкнуло к изучению математических приложений и онлайн-ресурсов.
Мы поговорили с сотнями преподавателей и просмотрели более 500 комментариев, чтобы узнать, какие математические инструменты они сочли полезными и бесполезными во время дистанционного обучения этой весной, а какие сократили для использования в новом учебном году.
Практика математических навыков
Ряд математических приложений и онлайн-инструментов могут помочь учащимся развить необходимое базовое понимание арифметических операций, которые им понадобятся в качестве основы для решения более сложных математических задач позже, рассказали нам учителя математики.
Чтобы помочь младшим школьникам практиковать такие навыки, как счет, сложение и вычитание, Эшли Блэквелдер, координатор Elementary STEAM в Южной Каролине, настоятельно рекомендует бесплатное приложение Moose Math для iPhone и iPad. В Moose Math учащиеся играют в математические игры, которые приносят им очки, чтобы помочь построить город.
Блэквелдер говорит, что детям легко ориентироваться в этом формате, и он отлично подходит для кратковременной концентрации внимания.
Дизайнер учебных программ и учебных пособий Кэсси Табризи порекомендовала веб-сайт Happy Numbers (от дошкольного до 5-го класса) на основе подписки (14 долларов США.50 долл. США на учащегося или 1 450 долларов США за сайт для новых школ), который разбивает математические уравнения, чтобы помочь учащимся понять математические концепции более высокого порядка. Чтобы использовать его, ученики превращаются в персонажей динозавров и решают математические задачи, чтобы вылупить яйца динозавров. Табризи сказала, что веб-сайт полезен, но рекомендует использовать его умеренно: ученикам может показаться утомительным, если они будут заниматься более 10 минут в день.
Учащиеся сражаются с монстрами в образе волшебника в Prodigy (1–8 классы), бесплатном игровом веб-сайте (также доступен в виде приложения для iPhone, iPad, iPod Touch и Android).Prodigy нравится детям, но не педагогам, потому что он больше основан на игре.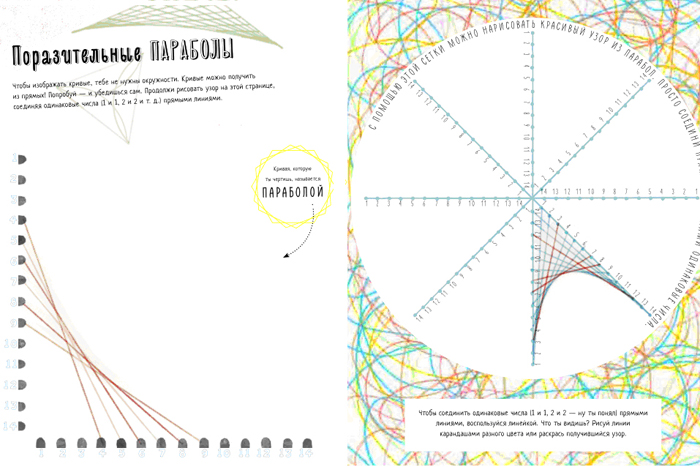
Бритни Пейдж, учительница пятого класса из Сиэтла, говорит, что, хотя это больше похоже на игру, ей нравится, что она автоматически нацелена на математические понятия, с которыми учащиеся сталкивались во время предварительного оценивания, и отслеживает, какой прогресс они добились в целевых областях. Большинство учителей предлагают Prodigy в качестве опции для студентов, если они заканчивают задание раньше срока.
Успешно решив математическую задачу, питомец студента произносит заклинание в бою.
Zearn (1–5 классы), бесплатная онлайн-программа для самостоятельного изучения, согласованная с Eureka Math — бесплатным учебным планом по математике от PreK до 12, — начинается с обычного урока с веселых разминочных упражнений, таких как сложение. сколько яблок съедает мультяшная лиса, заинтересовать учащихся. Работая по программе, учащиеся решают арифметические задачи на время, смотрят обучающие видеоролики по новым понятиям и решают практические задачи.
Шеннон Макграт, преподаватель из Вестерн-Спрингс, штат Иллинойс, говорит, что Zearn — это хорошая «концептуальная практика высокого уровня» и дает хорошие отзывы как учителям, так и ученикам, но иногда может слишком медленно прогрессировать для детей, которые быстро осваивают концепции.
Открытые математические задачи
Открытые математические задачи — задачи, которые обычно имеют более одного ответа — помогают учащимся развивать концептуальное понимание математики, а не зацикливаться на запоминании фактов, сказали преподаватели математики, с которыми мы разговаривали, которые постоянно упоминали три бесплатных веб-сайта, которые можно использовать для открытых математических задач. .
Open Middle (дошкольный – 12-й класс) оставляет части уравнения пустыми и просит учащихся заполнить их, чтобы оно было верным. «Мне нравится Open Middle для удаленного обучения, особенно в сочетании с Google Jamboard, — говорит МакГрат.«Задачи вдохновляют на исследовательское мышление, игровые игры, творчество и настойчивость».
Использование «Какому не принадлежит?» Студенты Мэри Бурасса, изучающие математику, приводят математический аргумент, почему каждый график лишний.
МакГрат также любит математику (дошкольный – 12-й класс) для создания сообщества. При использовании сайта учащиеся выбирают один из двух примеров из реальной жизни — например, коробку конфет с пятью рядами и 14 столбцами или коробку конфет с семью рядами и девятью столбцами — и должны привести математический аргумент, чтобы подтвердить свой выбор.
Какой из них не принадлежит? (pre-K–12 класс), аналогичный сайт, демонстрирует четыре фигуры, числа или графики и просит учеников описать, какая из них не принадлежит, используя математический словарь. «Это отлично подходит для начала синхронного обсуждения, поскольку считается задачей с низким уровнем пола и высоким потолком», — говорит Джозеф Манфре, специалист по математике из Департамента образования Гавайев.
Учительница математики средней школы Мэри Бурасса просит своих учеников, изучающих математику, определить причины, по которым каждый график в наборе из четырех не принадлежит, указывая характеристики графика, такие как асимптоты и недифференцируемые точки, а позже ее ученики создают свои собственные наборы WODB.
Богатые математические задачи
Для сложных математических задач — задач, которые поддаются строгости, сотрудничеству и концептуальному мышлению — преподаватели математики отметили пару веб-сайтов.
Предоставлено Брайаном Пенфаундом/Fraction TalksУчащиеся используют это изображение из Fraction Talks, чтобы попрактиковаться в сложении и умножении дробей. Нижняя угловая часть представляет собой ½ x ¼ = ⅛.
Fraction Talks (1–12 классы) — это веб-сайт, заполненный изображениями фигур — например, треугольников внутри треугольников, — которые поощряют математические дискуссии.Просто спрашивая студентов: «Что вы наблюдаете?» может подсказать им, что и сколько фигур они заметили, спрашивая: «Сколько фигур красных или заштрихованных?» побуждает учащихся изучать и понимать дроби.
Как только учащиеся получат базовое представление о дробях, они смогут приступить к изучению более сложных понятий. Предлагая учащимся смотреть на части фигуры и на то, какие дроби они получают при объединении, Брайан Пенфаунд помог своим ученикам седьмого и восьмого классов визуализировать сложение и умножение дробей.
Visual Patterns (K – класс 12) показывает начало шаблона, например, несколько прямоугольников в сетке, а затем просит учащихся составить уравнение, соответствующее шаблону. «Несмотря на то, что есть только один ответ, — говорит Манфре, — вы можете задавать более глубокие вопросы с помощью таких задач и вовлекать учащихся в математику в ее более естественной, наглядной форме».
Предоставлено Visual PatternsУчащиеся должны найти уравнение для этого шаблона.
Инструменты моделирования
По словам учителей математики, симуляции, такие как манипулирование выражением и просмотр изменений на графике, являются отличными инструментами, помогающими учащимся визуализировать математические концепции.
Эшли Таплин, специалист по математике средней школы, попросила своих учеников нарисовать, как они себя чувствовали в течение первой недели дистанционного обучения.
Апплеты — простой код с определенной целью — были упомянуты несколькими учителями как хороший ресурс. Студенты-статистики Эммы Чьяппетта используют апплеты с сайта RossmanChance.com, например, для манипулирования и определения шаблонов распределения выборки на графиках. Она создает базовое руководство о том, как использовать апплет, какие значения следует изменить, а затем задает вопросы, чтобы заставить учащихся критически осмыслить эти шаблоны.Кьяппетта также использует апплеты Массачусетского технологического института для своих студентов, изучающих линейную алгебру.
Desmos (6–12 классы) — веб-сайт с интерактивными математическими заданиями и графическим калькулятором (также доступен в виде приложения для iPhone, iPad, iPod Touch и Android) — еще один бесплатный инструмент, пользующийся популярностью среди учителей, как мы слышали.
Хотя социальное и эмоциональное обучение (SEL) и математика могут показаться несовместимыми, учителя интегрировали SEL в уроки математики с помощью Desmos. Например, в первую неделю дистанционного обучения Эшли Таплин, специалист по математике средней школы из Сан-Антонио, штат Техас, попросила своих учеников составить график своего самочувствия.Таплин говорит, что ей особенно нравится, что учителя могут выполнять свои собственные задания, например, о параболах и сортировке карточек, где учащиеся сопоставляют карточки с именем, соответствующим уравнением и правильным графическим представлением функции.
S.O.S. Математика — Интересные сайты в World Wide WebВот список некоторых хороших сайтов во всемирной паутине. Если вы знаете сайт, который должен быть указан, пожалуйста, сообщите нам об этом…. Сайты по общей математике
Онлайн-помощь, обучение и другие услуги
ОрганизацииПеред исчислением: арифметика и алгебра
Геометрия
ИсчислениеЗа пределами исчисления
КалькуляторыМатематическое программное обеспечение, системы компьютерной алгебры и Java-апплетыМатематические журналы в Интернете
Разное Сайты по математикеИнформация об университетах и школахПомощь научной ярмаркиДругие сайты
|
Этот сайт стоит посетить.
Веб-мастера проделали замечательную работу по сбору материала, связанного с математикой.
доступны в Интернете.
Очень хороший сайт!
[Ссылка мертва 01.02.09.]
(платно)
с упором на линейную алгебру. Вы можете скачать части книги или весь учебник!
7 Эффективное обучение: примеры из истории, математики и естественных наук | Как люди учатся: мозг, разум, опыт и школа: расширенное издание
Это означает, что новые учителя должны развивать способность «понимать педагогически рефлексивным способом; они должны не только разбираться в дисциплине по-своему, но и знать «концептуальные барьеры», которые могут помешать другим» (McDonald and Naso, 1986: 8). Эти концептуальные барьеры различаются от дисциплины к дисциплине.
Акцент на взаимодействии между дисциплинарными знаниями и педагогическими знаниями прямо противоречит распространенным заблуждениям о том, что учителя должны знать, чтобы создать эффективную среду обучения для своих учеников. Ошибочные представления состоят в том, что преподавание состоит только из набора общих методов, что хороший учитель может преподавать любой предмет или что достаточно только содержательных знаний.
Некоторые учителя способны преподавать различными способами.Однако их способность делать это требует большего, чем набор общих педагогических навыков. Рассмотрим случай с Барб Джонсон, которая 12 лет работала учительницей шестого класса в средней школе Монро. По общепринятым меркам Монро — хорошая школа. Результаты стандартизированных тестов примерно средние, размер класса небольшой, помещения в здании содержатся в хорошем состоянии, администратор является сильным учебным руководителем, а текучесть кадров и преподавателей незначительна.
Тем не менее, каждый год родители посылают своих учеников пятого класса из местных начальных школ в Монро-жокей, чтобы записать своих детей в классы Барб Джонсон.Что происходит в ее классе, что дает ему репутацию лучшего из лучших?
В течение первой недели в школе Барб Джонсон задает своим шестиклассникам два вопроса: «Какие у вас есть вопросы о себе?» и «Какие у вас есть вопросы о мире?» Учащиеся начинают перечислять свои вопросы: «Могут ли они быть о глупых мелочах?» — спрашивает один из студентов. «Если это ваши вопросы, на которые вы действительно хотите получить ответы, то они не глупые и не маленькие», — отвечает учитель.После того, как учащиеся перечислят свои индивидуальные вопросы, Барб организует их в небольшие группы, где они обмениваются списками и ищут общие вопросы. После продолжительного обсуждения каждая группа составляет приоритетный список вопросов, ранжируя вопросы о себе и о мире.
Снова вместе на групповом занятии Барб Джонсон выясняет приоритеты групп и работает над достижением консенсуса по объединенным спискам вопросов класса.
Эти вопросы становятся основой для руководства учебной программой в классе Барб.Один вопрос: «Доживу ли я до 100 лет?» породил образовательные исследования в области генетики, семейной и устной истории, актуарной науки, статистики и вероятности, болезней сердца, рака и гипертонии. Студенты имели возможность искать информацию у членов семьи, друзей, специалистов в различных областях, в онлайновых компьютерных сервисах и книгах, а также у преподавателя. Она описывает то, что им пришлось сделать, как стать частью «обучающегося сообщества». По словам Барб Джонсон, «мы решаем, какие интеллектуальные проблемы являются наиболее важными, и разрабатываем способы исследования этих проблем
4 Оценка для поддержки обучения математике | Измерение того, что имеет значение: концептуальное руководство по оценке математики
, как правило, подсчитывая количество вопросов, на которые были даны правильные ответы, и сравнивая баллы одного человека с баллами другого на основании их относительного процентиля.
Так называемые нормативные баллы волнуют педагогов уже много лет. Несмотря на то, что высказывались различные критические замечания по поводу ссылок на нормы, главная образовательная проблема заключается в том, что такая информация недостаточно полезна для улучшения обучения и обучения и может фактически иметь контрпродуктивные образовательные последствия. В классе преподаватели и учащиеся должны знать, что учащиеся понимают хорошо, а что хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных учащихся могут использоваться вне контекста классной комнаты, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.
Программы оценивания должны информировать учителей и учащихся о том, что учащиеся узнали, как они учатся и что они думают о математике. |
Например, чтобы спланировать свое обучение, учителя должны знать о текущем понимании каждым учеником того, что будет преподаваться.
Таким образом, программы оценивания должны информировать учителей и учащихся о том, чему они научились, как они учатся и что они думают о математике.Чтобы эта информация была полезной для учителей, она должна включать анализ конкретных сильных и слабых сторон понимания ученика, а не просто оценки вне контекста.
Чтобы обучение было эффективным, результаты оценки должны быть своевременными. 35 Учебе учащихся не способствуют компьютерные распечатки, отправляемые учителям после окончания учебного года и ухода учащихся, а также учителя, которые тратят слишком много времени на выставление оценок.В частности, должны быть найдены новые способы дать учителям и учащимся более непосредственную информацию об успеваемости учащихся по оценкам, предписанным внешними органами, чтобы эти оценки, а также собственные оценки учителя, можно было использовать для улучшения обучения. Даже если основной целью оценки является определение достижений школы, штата или страны, оценка должна предоставлять отчеты об их работе участвующим в ней учащимся и учителям.
Школьное время бесценно.Когда учащимся не сообщают об их ошибках и неверных представлениях, не говоря уже о том, чтобы помочь их исправить, оценивание может как усугубить непонимание, так и растратить драгоценное учебное время.
Когда форма оценки незнакома, учителя несут особую ответственность перед своими учениками, сообщая им об этом заранее
Математика ЭКГ: ряды Фурье
Недавно я проходил медицинское обследование, которое включало ЭКГ (электрокардиограф).
Вот так выглядела моя ЭКГ:
[Щелкните изображение, чтобы увеличить его.]
Как делается ЭКГ
Электроды подключаются к различным анатомическим частям (грудной клетке, ногам, рукам, ступням) и измеряются разности напряжений во времени для получения данных ЭКГ.
Горизонтальная ось распечатки ЭКГ представляет время, а вертикальная ось — амплитуду напряжения.
Единицами амплитуды являются милливольты (мВ), а на графике 1 мВ = 10 мм в высоту.
Шкала времени 25 мм = 1 секунда (или 1 мм за 0,04 секунды на графике).
Итак, вот мои показания для Отведения II , представляющие напряжение между положительным электродом на моей левой ноге и электродом на моей правой руке. Каждая более толстая красная вертикальная линия представляет время в 1 секунду.
Судя по всему (по словам врача), это указывает на то, что мое сердце вполне здорово.
Более подробно особенности рассматриваемого нами повторяющегося импульса следующие.
[Источник изображения: Т. Берк]
Зубец P вызван сокращением правого предсердия, за которым следует левое предсердие (камеры в верхней части сердца).
Комплекс QRS представляет собой момент времени, когда большая часть сердечных мышц работает, поэтому имеет наибольшую амплитуду.
Зубец T представляет собой поляризацию желудочков (камер на дне сердца).
Сердце человека с изображением предсердий и желудочков.
[Изображение предоставлено UCSD, исходная страница больше недоступна]
Моделирование сердцебиения с помощью ряда Фурье
Сердцебиение примерно регулярное (если это не так, это указывает на то, что что-то не так).Математически мы говорим, что что-то, что регулярно повторяется, называется периодическим .
Такие волны можно представить с помощью ряда Фурье.
Предположения
В моем случае пульс был около 70 ударов в минуту. Для простоты я приму 60 ударов в минуту или 1 удар в секунду. Таким образом, период = 1 секунда = 1000 миллисекунд.
Также для простоты я буду моделировать только R wave для этой статьи. Чтобы получить более точную модель сердцебиения, мне просто нужно выполнить аналогичный процесс для зубцов P, Q, S и T и добавить их в мою модель.
Я заметил, что мой зубец R имел высоту около 2,5 мВ и длился в общей сложности 40 мс. Форма зубца R почти треугольная, поэтому я мог бы использовать прямые линии для своей модели, но они не дают нам плавной кривой (особенно вверху — она должна быть непрерывно дифференцируемой).
Лучший подход — использовать полином (где восходящие и нисходящие линии достаточно близки к прямым), поэтому моя модель выглядит следующим образом (единицы времени — миллисекунды):
f ( t ) = -0.0000156( т − 20)⁴ + 2,5
f ( t ) = f ( t + 1000)
Описание модели
Модель основана на квартике (степень 4), так как это даст мне близкую к нужной мне форму (парабола была бы слишком широкой). Я использую то же мышление, что и в этой статье, где я перемещаю кривую туда, куда мне нужно.
Член ( t − 20) исходит из решения, что кривая должна начинаться с (0,0) (что облегчает нашу жизнь), она будет проходить через (40,0), поскольку длительность импульса составляет 40 мс, и центрироваться на t = 20.
«+2,5» происходит из-за того, что амплитуда импульса составляет 2,5 мВ.
-0,0000156 получается из решения следующего для a , когда t = 0,
a ( t − 20)⁴ + 2,5 = 0,
Часть « f ( t ) = f ( t + 1000)» означает, что функция (импульс в данном случае) повторяется каждые 1000 мс.
График модели
Это график части одного периода (часть выше t -ось от t = 0 до t = 40):
Конечно.это всего лишь один импульс. Как построить график, который повторяет этот импульс через равные промежутки времени?
Здесь мы используем ряды Фурье.
Я избавлю вас от подробностей, но, по сути, ряд Фурье — это бесконечный ряд, включающий тригонометрические члены. Когда все члены добавлены, вы получаете математическую модель исходной периодической функции.
Чтобы получить ряд Фурье, нам нужно найти среднее значение , a 0 и 2 выражения коэффициентов, включающие n , a n и b 3 . тригонометрические члены и суммируются для n = 1 до бесконечности.
Среднее значение Срок
a 0 получается путем интегрирования следующим образом ( L — половина периода):
(Участок кривой, который нам нужен для этой части задачи, находится от t = 0 до t = 40, поэтому мы выбрали эти значения для пределов интегрирования в предпоследней строке.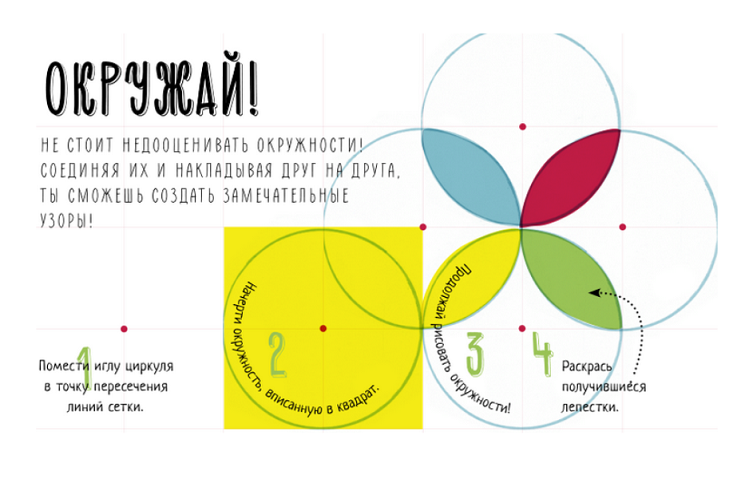
)
Первый коэффициент,
a nДалее мы вычисляем a n :
Ответ для этого интеграла довольно уродлив.Я включил его в решение PDF.
Второй член коэффициента,
b nТеперь для b n :
И снова я избавил вас от подробностей.
Наконец, мы собираем все вместе и получаем Ряд Фурье для нашей простой модели сердцебиения:
Если мы нарисуем это только для первых 5 членов ( n = от 1 до 5), мы увидим начало регулярного 1-секундного сердечного сокращения.
На приведенном выше графике показан «шум» при разложении в ряд Фурье, особенно если вы взяли недостаточно членов.
Принимая больше терминов (на этот раз добавляя первые 100 терминов), мы получаем следующее, и мы видим, что получаем разумное приближение для обычного зубца R с периодом 1 секунда.
Я добавил T wave для этой следующей модели (синий).
Я использовал параболу для зубца T, потому что форма зубца T шире, чем форма зубца R.
Мы могли бы продолжить, добавив волны P, Q и S, чтобы получить еще лучшую модель.
См. полное решение (вплоть до зубца Т, созданное с помощью журнала Scientific) здесь:
Модель сердцебиения человека (PDF)
Что мы сделали?
Мы взяли один пик, представляющий один зубец R моего сердцебиения. Затем мы нашли формулу, которая повторяет наш всплеск через равные промежутки времени. Ряд Фурье (бесконечная сумма тригонометрических членов) дал нам эту формулу.
Наконец, мы добавили зубец T, используя ту же теорию, что и раньше.
СерияФурье очень полезна в электронике и акустике, где сигналы имеют периодические формы.
Чтобы узнать больше о рядах Фурье, перейдите по ссылке:
.Серия Фурье
Не пропустите раздел об использовании Фурье для создания цифрового звука в
.