Обведи линией пару фигур у которых одинаковая форма: Основные геометрические фигуры 🟢🟨🔺 и их названия

учим плоские и объемные геометрические фигуры

Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.

Конечно, нам может казаться, что ребенок слишком  мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.

Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно. Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.

Зачем ребенку учить геометрические фигуры?

Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений.

Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.

Знание геометрических фигур помогает:

• развивать пространственное мышление, ориентацию в пространстве;
• расширять кругозор;
• развивать способность сравнивать, анализировать, обобщать и выделять главное, классифицировать;
• пополнять словарный запас.

И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.

Как учить геометрические фигуры с дошкольником?

1. Обучение для дошкольников должно строиться в виде увлекательной игры.
2. Не нужно ругать ребенка, если он не запомнил названия фигур с 1 раза, даже если с 31 – не стоит.
3. Не забывайте органично вплетать геометрические познания в жизнь: «подай квадратную коробочку», «возьми яблоко с круглой тарелки».
4. По дороге в сад ищите предметы прямоугольной или круглой формы, соревнуйтесь, кто больше найдет и назовет.
5. В игровом арсенале у вас должны быть игрушки правильной геометрической формы — мячи, кубики, детали конструктора.
6. Обычно малыши любят помогать маме на кухне. Приобретите круглые, квадратные, прямоугольные формочки и испеките съедобные геометрические фигуры.
7. Важно при изучении фигур задействовать и тактильную память. Ребенку гораздо интереснее будет не только увидеть, но и пощупать, погладить, а может еще и лизнуть объект изучения.
8. Нагружайте мозг ребёнка дозировано, постепенно дополняя информацией. Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».

Основные техники и методики запоминания фигур

Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.

1. До достижения 1,5 лет проговариваем вслух окружающие предметы, снабжая свой рассказ информацией о форме (давай возьмем круглое яблоко).
2. В возрасте 1,5 — 2 лет пользуемся картинками, раскрашиваем фигуры, используем сортеры для изучения фигур. Начинаем с самого простого — круга. Остальные фигуры будем подключать только после того, как ребенок усвоил понятие «круг».
3. С 2 лет до достижения школьного возраста можем применять все существующие методики, следуя от простого к сложному.

При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал. Знания этих фигур доступны для детей 2-3 лет.

Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.

Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.

Разберем некоторые варианты техник по изучению геометрических фигур:

1. Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.

2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.

3. Объемные наклейки и магниты, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.

4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.

5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.

6. Обводить пунктирные геометрические фигуры.

7. Раскрасить или заштриховать предложенные вами геометрические фигуры.

7. Дорисовать фигуру по образцу.

8. Рисовать фигуры при помощи трафаретов.

9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.

10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.

11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру. Задача ребенка обнаружить и назвать, какой фигуры нет.

12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.

13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.

14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.

15. Подвижные игры. Например, на асфальте рисуются овал, треугольник, квадрат, прямоугольник. По команде взрослого ребенок должен найти названную фигуру и встать в неё.

16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.

17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.

Учим объемные геометрические фигуры

Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:

1. Найти объемную фигуру по плоскому образцу — отличное упражнение на развитие пространственного мышления.
2. «Сыщик». Детям раздают «ориентировку» – плоский рисунок искомой фигуры со всех сторон. Детям необходимо сопоставить картинки и найти нужную фигуру.
3. Создать трехмерную модель самому. Взрослый может распечатать трафареты с интернета. Ребенку остается согнуть по линиям и склеить, чтобы получилась фигура.
4. Макеты, оригами –  можно попробовать с вместе с ребенком создать свою объемную игрушку из бумаги.
5. Конструктор. Постройте при помощи деталей башню или замок для принцессы. Эта игра будет способствовать развитию мелкой моторики, воображению, пониманию свойств объемных фигур.

Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

Изображение геометрических фигур разных видов и размеров.

Как в игровой форме научить малыша узнавать геометрические фигуры? Зачем ребенку изучать геометрические фигуры

Умеете ли вы составлять животных из геометрических фигур?

Никогда не пробовали?

Тогда стоит посмотреть картинки на сайте, где из геометрических фигур сложены разнообразные животные. Предложите эти рисунки своим детям: наверняка они оценят их оригинальность.

Геометрический мир

Во всем, что нас окружает, можно отыскать элементы геометрии.

Стол может быть круглым или квадратным, наши дома – параллелепипеды и т.д. Не наблюдали, как рисуют художники? Они сначала намечают контуры предмета с основой из геометрических фигур, а уж затем проводят вокруг них плавные линии. Они видят мир геометрическим, а ровные или мягкие линии лишь скрывают настоящую суть вещей.

В педагогике для детей дошкольного возраста есть даже целое направление, где ребят учат во всем видеть чистые геометрические фигуры. Это педагогика Марии . Она считала, что чистые геометрические фигуры способствуют лучшему развитию детей и их ориентации в мире. Нельзя сказать, что эта система идеальна, но она нашла своих сторонников.

А теперь давайте вспомним произведения художников эпохи модернизма и постмодернизма. Перед глазами встают картины, наполненные квадратами, треугольниками, кругами, трапециями и всевозможными фигурами, окрашенными в разные цвета. Так живописцы новой эпохи видели мир, и этому должно было основание. Они пытались передать этот мир нетронутым человеческими руками. Их стремлением было показать, что все мы и все предметы вокруг нас состоят из геометрических фигур. Весь наш мир, если присмотреться, — сплошная геометрия.

Как использовать картинки в работе с детьми

Вполне понятно, что встает вопрос: одно дело художники, но зачем детям такое видение мира?

Конечно, картинки с животными из геометрических фигур не ставят целью навязать малышу неординарное видение мира. Однако почему бы ни показать, что и такая трактовка всего, что нас окружает, возможна.

По картинкам можно интересно и увлекательно изучать названия геометрических фигур. От простого показа и повторения ребенок быстро устает и начинает отказываться от занятий, даже если их проводит мама в домашних условиях. Другое дело, если фигуры необходимо отыскать в животных. Тут просыпается неподдельное любопытство.

Когда вы полностью изучите с ребенком названия фигур и их внешний вид, попросите ребенка проявить свое видение мира. Пусть для примера будет взято животное или любой предмет.

Спросите: на какую геометрическую фигуру он похож.

Такие упражнения:

1. — развивают наблюдательность;
2. — совершенствуют логическое и пространственное мышление;
3. — способствуют видению скрытого за внешней оболочкой предмета.

Малыш учится видеть и наблюдать то, что не могут или не умеют видеть другие . Это ли не воспитание художника и творческой личности?

А можно поиграть в обратную игру. Представьте, что вы художники-абстракционисты. Пусть один из вас нарисует что-нибудь, состоящее из геометрических фигур, а другой попытается отгадать, что нарисовано. Живописцы постмодернизма часто зашифровывали свои рисунки на полотне, заполненной квадратами, прямоугольниками, трапециями… такие же головоломки предлагали ранее детские журналы.

Вы и сами можете создать такую головоломку: нужно лишь немного фантазии и взгляд на мир сквозь призму геометрии.

Нажмите на картинку, чтобы скачать эту тетрадку с заданиями для детей бесплатно.
Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет.

Аппликации для детей от 4 до 7 лет. Нажмите на картинку, чтобы скачать эту книгу.

Изучение геометрии с маленькими детками – процесс довольно забавный, ведь в этом возрасте они набираются опыта и пополняют багаж имеющихся знаний. А изучение фигур помогает также развивать мышление и память. Как же правильно «преподнести» геометрические фигуры детям 3–4 лет?

Действуем поэтапно

Итак, геометрические фигуры имеют важное значение для развития детей. Чтобы их освоение было успешным, стоит воспользоваться следующими правилами.

• Знакомство начинаем с простейших фигур (это будут круг, треугольник и квадрат).
• На начальном этапе лучше, чтобы все фигурки были одного цвета и размера, дабы не отвлекать малыша лишними деталями.
• Помним о возрасте (в 2 года осваиваем только круг, квадрат и треугольник; к 3 годам добавляем овал, ромб, прямоугольник; к 4 – трапецию, звезду, пяти- или шестиугольники).
• Обучение должно быть многогранным, чтобы ребенок постоянно закреплял полученные навыки (обводим форму пальцами, учимся находить фигуры вокруг и различать, сортируем их по виду, размеру, создаем и анализируем аппликации, лепим, вырезаем, играем с карточками или лото, закрепляем формы в активных играх).

Начинайте изучение с плоских изображений, постепенно показывая ребенку разницу между плоскостью и объемом, уча сопоставлять объемное геометрическое тело с его плоскостным изображением.

С чего начать изучение?

Для начала можно познакомить ребенка с изображением круга: обвести пальчиками, рассказать, что это. Через день начать искать вокруг себя все, что его напоминает. Если малыш затрудняется, родители должны ему помочь. Следующие фигуры изучают аналогично.

Затем следует объяснить ребенку, что объемные фигуры похожи на плоские (квадрат – на кубик, круг – на мяч). Пусть попробует соотносить их, находя аналогии вокруг себя. Для этого полезно показывать малышу плоское изображение, прося достать из мешочка такой же предмет, но объемный, а также искать «спрятавшиеся» фигуры на прогулке, при чтении книг или просмотре мультиков.

Хорошо помогает закрепить полученные знания специальное «геометрическое» лото: карточки с геометрическими фигурами, которые нужно располагать по местам на игровой карте. Лото можно изготовить самостоятельно. Для начала карточки берут одноцветные. Позже можно добавить другие цвета – так сложнее найти нужную пару.

Также этому способствует тактильное воссоздание заданной формы: рисование, лепка, выкладывание из разных предметов, вырезание, мозаика, аппликация. По мере освоения все новых фигур аппликации могут становиться более сложными: не просто квадратики на квадратном листе или круги на круглом, а целые картины, состоящие из разных фигур. Создавая их, нужно проговаривать, какая фигура какой частью композиции будет служить (круг – солнцем или колесом, треугольники – елочками, крышей и т. д.).

Совершенствуем и закрепляем

Изучение геометрических фигур для дошкольников ближе к 4 годам должно постоянно усложняться. Например, малыш уже должен научиться различать фигуры по форме и размерам, а также по тем действиям, которые с ними можно производить (катать, складывать в башню). Немного позже он научится сортировать геометрические тела по двум признакам (какие геометрические предметы получится катать, но не получится ставить друг на друга, или какие предметы нельзя покатить, но можно выстроить в башенку).

Закреплять полученные геометрические знания полезно в форме активных игровых занятий, во время которых ребенок должен двигаться по определенной траектории (обойти круг, обползти квадрат, «обпрыгать» треугольник, нарисованные на асфальте). Затем, когда такие игры будут освоены, их усложняют (пройти, держа в руках ложку с мячиком, пробежать, ведя по земле мяч).

Все это поможет ему более полноценно подготовиться к обучению к школе, развить память, пространственное и логическое мышление. Главное – заниматься с ребенком систематически.

Предлагаем вашему вниманию развивающее упражнения для детей 5 — 6 лет, которое в доступной и занимательной форме поможет ребенку освоить основы геометрии, а также развить зрительное и слуховое восприятие, произвольное внимание, память, логическое и пространственное мышление.

Занятие с ребенком этого возраста должно длиться не более 25 — 30 минут. Объясните малышу задание, при необходимости помогите в его выполнении. Убедитесь, что задание выполнено верно.

Для работы малышу потребуются цветные карандаши или фломастеры.

Не забудьте проследить за правильной осанкой малыша, а также похвалить его за старание.

Успехов вам и вашим детям!

Задание №1

Раскрась фигуры так, чтобы круг лежал на квадрате.

Задание №2

Раскрась фигуры так, чтобы треугольник лежал на трапеции.

Задание №3

Раскрась фигуры так, чтобы овал лежал на ромбе.

Задание №4

Раскрась фигуры так, чтобы пятиугольник лежал на прямоугольнике.

Задание №5

Найди продолжение каждой цепочки. Соедини начало и конец цепочки. Раскрась их. Из каких фигур они состоят?

Задание №6

Нарисуй в пустых клетках фигуры, на которые похожи эти предметы. Назови фигуры.

Задание №7

Соедини предметы линиями с похожими на них геометрическими телами.

Задание №8

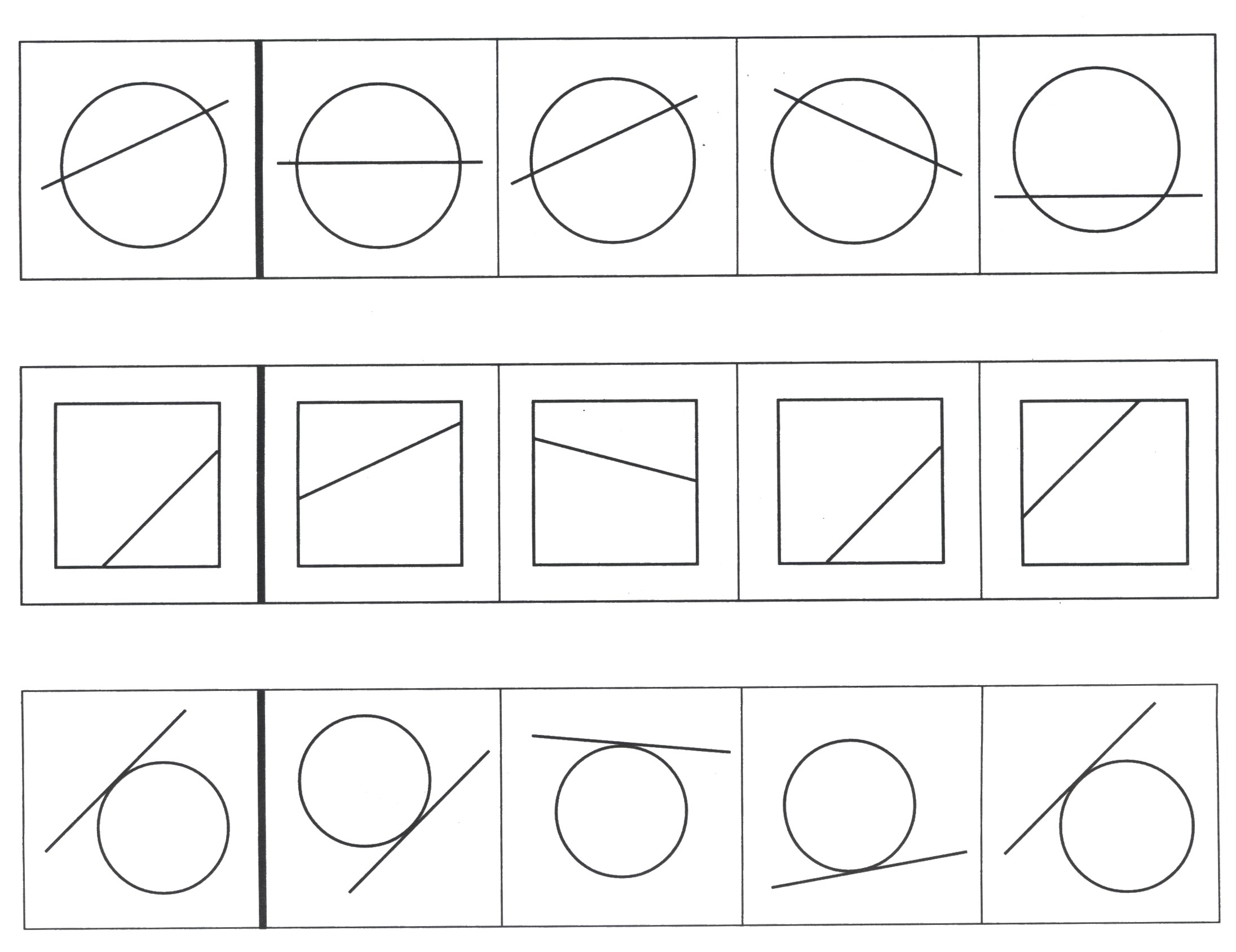
Обведи прямые линии красным цветом, кривые — синим, ломаные — зелёным.

Задание №9

Выполни штриховку круга вертикальными линиями, квадрата — горизонтальными, треугольника — наклонными.

Задание №10

Здесь нарисованы разные линии, и среди них — ломаные. Найди и сосчитай ломаные линии. Сосчитай их звенья. Посмотри, что нарисовал художник на концах ломаных линий. Нарисуй на противоположных их концах такие же предметы.

Задание №11

Продолжи ломаные линии так, чтобы получились различные предметы. Назови, что у тебя получилось.

Задание №12

При помощи линейки соедини точки так, чтобы получились многоугольники. Многоугольник, у которого все углы прямые, раскрась красным цветом. Многоугольник, у которого все углы тупые, раскрась синим цветом. Объясни, почему одна фигура осталась нераскрашенной.

Задание №13

Поставь цветными карандашами точки в местах пересечения линий.

Задание №14

Обведи в каждом ряду лишнюю линию. Объясни, чем она отличается от других.

Задание №15

Обведи прямые углы красным карандашом, острые зеленым, а тупые — синим.

Задание №16

Красным карандашом обозначь вершины многоугольников, а синим — стороны многоугольников.

Задание №17

Зачем маленького ребенка обучать геометрическим фигурам? Наверняка, многие родители даже не задумываются над этим вопросом, просто отдавая дань моде и обучая кроху математике чуть ли не с рождения. Между тем, геометрические фигуры для детей, их своевременное изучение играют большую роль в познании окружающего, знакомя с одним из основных свойств предметов — формой. Это необходимо для развития логического мышления, пространственных представлений, совершенствования математических способностей. Вот почему важно начинать ознакомление с геометрическими фигурами как можно раньше, подкрепляя знания ребятишек увлекательными заданиями в повседневной жизни.

Что должен знать ребенок о геометрических фигурах

Важно: Геометрические фигуры — общепринятые эталоны, меры измерения формы предметов. Поэтому домашнее ознакомление ребенка с формами должно проходить не отдельно, а в системе сенсорного (чувственного) воспитания. Лучше всего кроха запомнит форму, когда параллельно рассматривает цвет, величину, назначение предмета, так как в разнообразной деятельности знания активно используются и лучше запоминаются.

Учим геометрические фигуры с малышами: главные правила

Важно: Как научить ребенка называть и различать геометрические фигуры легко и быстро! Для этого нужно придерживаться определенных правил. При хаотичном, непоследовательном обучении малыш может путать фигуры, не видеть их похожесть и различность.

Загадки в стихах

Нет углов у меня и похож на блюдце я, на тарелку и на крышку, на кольцо и колесо. Кто же я такой, друзья? Назовите вы меня (круг).

Он давно знакомый мой, каждый угол в нем прямой. Все четыре стороны одинаковой длины. Вам его представить рад. Как зовут его? (квадрат).

На фигуру посмотри и в альбоме начерти, три угла, три стороны меж собой соедини. Получился не угольник, а красивый (треугольник).

Вот такая есть окружность — очень странная наружность. Круг приплюснутым стал, получился вдруг (овал).

Растянули мы квадрат и представили на взгляд. На кого он стал похожим или с чем-то очень схожим?
Ни кирпич, ни треугольник — стал квадрат (прямоугольник).

Сказка «Два брата» (взрослый рисует под ритмику стиха)

Давным-давно в темном лесу в фигурной избушке жили-были два брата, два квадрата. И были они близнецами. Убедитесь сами:
Видите на картинке — у каждого 4 стороны, 4 угла и 4 вершинки.
Гулял как-то первый квадрат между кустами, стучал по дорожке четырьмя уголками.
А звери говорят: «Кто это? Первый квадрат или его брат, второй квадрат? Как же они похожи!
Помните на картинке: 4 стороны, 4 угла и 4 вершинки.
Надоело квадрату, что его путают с братом, и решил он измениться, в другую фигуру превратиться.
Взял он ножницы и срезал себе четыре уголка. В круг превратился и по дорожке покатился.
И живется теперь братьям чудно, перепутать теперь братьев трудно:
Один катается по дорожкам, другой ходит на четырех уголках — четырех ножках.
До сих пор дружат два брата — круг с квадратом!

Важно: Особенности восприятия детьми геометрических фигур совсем не такие, как у взрослых. Например, взрослый видит предметы сообразно формам (кастрюля — цилиндр, окно — прямоугольник). Ребенок, наоборот, сначала форму опредмечивает (квадрат — воздушный змей, треугольник — крыша дома, круг — мячик, несколько кругов — очки, бусы). При правильном обучении он начинает абстрагироваться от предметов и воспринимать в окружающем знакомую фигуру, например, стакан как цилиндр (цилиндрической формы), крыша как треугольник (треугольной формы), мяч как шар (круглой формы).

Играем с геометрическими формами!

Педагоги напоминают, что основные знания о геометрических фигурах дошкольники получают в детском саду, а домашние занятия направлены на закрепление изучаемого. Поэтому самым лучшим средством дома будет игра, как основная деятельность малышей. Именно в игре ненавязчиво, легко и быстро ребенок выучит все названия фигур, научится их сравнивать и различать. Среди развивающих игр на обучение геометрическим формам первенство принадлежит настольным играм. В них можно играть по вечерам, во время семейного досуга, сделать частью любого домашнего занятия, развлечения.

«Что спряталось»

Классическая игра понятна и доступна даже двухлетнему крохе. Взрослый раскладывает перед ребенком изображения знакомых фигур: круг, квадрат, треугольник. Так как карточек должно быть не меньше пяти, для количества используются фигуры разных цвет и размеров, например, два квадрата — большой и маленький, два треугольника — синий и желтый, один круг. Рассмотреть их с ребенком, обсудить, убедиться, что понимает, какие фигуры перед ним и может их правильно назвать. Затем малыш закрывает глаза, взрослый прячет одну из фигур и спрашивает, что спряталось. С возрастом количество фигур увеличивается, к старым добавляются новые.

«Одним словечком»

Игра «геометрические фигуры» направлена на формирование у детей обобщения однотипных фигур. Взрослому нужно подготовить круги, квадраты и треугольники разного размера и цвета. Дошкольник должен распределить по группам представленные фигуры независимо от цвета и размера, назвать их обобщающим словом, например, все квадраты. Как вариант, можно усложнять задания, предлагая сгруппировать фигуры только по цвету или размеру.

«Чудесный мешочек»

Игры по типу «чудесного мешочка» хорошо знакомы ребятишкам детсадовского возраста. Они полезны тем, что дают представление о контурах предметов, обучают обследованию на ощупь и упражняют в различении форм. Взрослый готовит мешочек с предметами разных форм, например, кубик, шарик, мячик, кирпичик, конусная пирамидка. Игрок обследует их и называет форму игрушки, которую хочет достать. Для усложнения задания старшим деткам предлагается найти какую-либо конкретную форму, например, «Найди круглую игрушку».

«Волшебные очки»

Предварительно готовятся импровизированные очки из плотной бумаги разной формы: круглые, квадратные. Игра интересна всем ребяткам, помогает расширить представления о геометрических фигурах, находить предметы определенной формы в окружающем пространстве. Например, ребенок надевает круглые очки и ищет все круглое вокруг себя: тарелка, дно у вазы, плафон у люстры, ковер, бабушкины очки. За каждый правильный подбор игрок награждается фишкой, а затем получает поощрительный приз в конце игры.

«Латки — заплатки»

Для занятия по закреплению представлений о геометрических фигурах нужна подборка картинок с изображением различных предметов, в которых есть «дырки» — незакрашенные места разной формы, например, у платья круглая дырка, в сапожке — квадратная. Среди разных «заплаток» ребенок выбирает нужную и соединяет с предметом. Интересно будет, если взрослый сам приготовит для игры изображения, например, вырежет из бумаги вещи (свитер, юбка, брюки, сапожки, шапочку). Как вариант игры в «латки — заплатки», можно приобрести дидактическую игру в «липучки», которые очень похожи правилами и содержанием

«Что сломалось»

Такое задание поможет приучить детей замечать, какой формы не хватает в изображенном предмете, развивает внимание. Для игры можно использовать картинки, аппликацию из вырезанных деталей, строительный материал. Главное — предмет должен состоять из частей геометрической формы. Например, взрослый выкладывает аппликацию «дом», где деталями являются треугольник — крыша, прямоугольник — стена, квадрат — окошко, маленький прямоугольник — дверь, круг — окошко в чердаке, четырехугольник — труба. Ребенок внимательно рассматривает изображение и закрывает глаза, взрослый убирает какую-либо деталь, смешивая ее с любыми другими. Нужно отгадать, что сломалось у домика и «починить», отыскав недостающую часть. В дальнейшем можно усложнить задание, сразу же не добавляя определенную форму или убирая две формы одновременно. Если это нарисованное изображение, то ребенок подрисовывает недостающие детали, например, круг — колесо у машины, прямоугольники — окошки у башенки.

«Игра с палочками»

Интересное задание для средних и старших дошкольников, одновременно развивает моторику и умение составлять геометрические фигуры. Если нет счетных палочек, можно использовать спички или зубочистки, предварительно их подготовить, обрезать серную головку или острые концы, чтобы малыш не поранился. Такое задание можно провести в виде соревнования во время семейного досуга, «кто быстрее всех составит фигуру?», «у кого самая сложная фигура?». Затем отметить призом победителя. Обязательно в какой-то момент им должен стать ребенок. Взрослый, например, может отметить его оригинальное решение или тщательно и аккуратно выложенную фигуру.

«Что пригодилось художнику в картине»

Для старших дошколят можно использовать оригинальное задание на рассматривание картин, которое не только закрепляет название фигур, но и развивает зрительное восприятие, умение видеть разные формы в необычной обстановке. Взрослый подбирает иллюстрации соответствующего содержания, которые художник рисует при помощи геометрических форм. Затем предлагает дошкольнику рассмотреть картинку м найти знакомые формы. Если какие-либо из них пока еще незнакомы дошколенку, обязательно обратить на них внимание и рассказать, как они называются, какие предметы похожи на них. Усложняя игру, можно посчитать, сколько геометрических фигур понадобилось для изображения картины.

«Геометрическое лото»

Классическое задание на ознакомление детей с геометрическими фигурами учит сравнивать форму предмета с геометрической фигурой, подбирать изображения в опоре на эталон. Чтобы получился соревновательный момент, интересный ребятишкам, играть лучше всей семьей. Правило классическое: на больших карточках — изображения разных фигур, например, овал, круг, треугольник. Ведущий произносит название предмета на маленькой карточке, например, яблоко, огурец, платок, телевизор. Игроки ищут на своей карточке форму названого предмета и закрывают ее соответствующей картинкой. Выигрывает игрок, который быстро и правильно закроет карточку.

«Геометрическая мозаика»

Такая развивающая игра поможет ребятишкам закреплению представлений о геометрических фигурах. Кроме того, научит дошколят преобразовывать их, ориентируясь на эталон (образец), поможет творческому воображению. Правила игры просты и доступны ребяткам любого возраста, для старших — количество деталей увеличивается, усложняются сюжеты. Игроки должны собрать из нескольких геометрических фигур какие-либо предметы. Для малышей это могут быть домики разной величины и конфигурации, машины, башенки, мостики, солнышко, цветы, узоры; для старших ребятишек — фигурки сказочных или мультяшных персонажей, сюжетные картинки: ваза с цветами, улица, дорога, ковер, животные, люди разных профессий. Обязательно отметить творчество дошколенка, похвалить его. Возможно, оставить выложенную картинку на некоторое время, чтобы показать всем близким. Главное, что такую развивающую мозаику можно приобрести в специальном магазине, а можно сделать своими руками по типу игрушек Монтессори.

Как познакомить ребенка с геометрией?

Геометрия — наука, с которой можно и нужно обучать деток с самого раннего возраста.

На данной страничке представлена подборка материалов — карточки, раскраски, темы для заданий, игры, при помощи которых вам будет легко познакомить ребенка с основными геометрическими формами и фигурами.
Все материалы вы можете открыть, скачать и распечатать по прямым ссылкам.

Карточки с геометрическими фигурами и формами

Яркие карточки с самыми основными геометрическими фигурами и формами. Карточки можно использовать, как наглядное пособие на первом занятии.

Геометрия для детей — раскраски, прописи, рабочая тетрадь

1.Тетрадь-раскраска для детей 3-5 лет. На каждой странице тетради простые графические упражнения и задания.
Скачать

2. Рабочая тетрадь в 2ух частях с понятными и интересными заданиями для детей 3-4 лет. Выполняя задания, ребенок познакомится с геометрией и узнает названия геометрических фигур и форм.
Скачать Скачать
3. Еще одна очень хорошая тетрадь для ознакомительных занятий с геометрией для детей 4-5 лет. В тетради много увлекательных и забавных заданий, выполняя которые ребенок легко усвоит начальные основы и понятия геометрии.

4. Тетрадь с обучающими и развивающими заданиями для детей 6-7 лет.
В тетради ребенку предлагается выполнить не сложные графические задания. Ребенок учится работать с линейкой и циркулем.
Скачать

Книги о геометрии для детей

1. Занимательная книга в стихах «Весёлая геометрия для самых маленьких» — автор Александр Тимофеевский.

Смешные и задорные стихи помогут малышам быстро познакомиться и запомнить много важной информации о геометрических фигурах и о масштабе предметов.
В весёлых стихах А. Тимофеевского юмор и шутка помогут маленькому читателю соотнести пока непонятные геометрические понятия с давно привычными бытовыми предметами. Дети увидят в юбке трапецию, в тарелке круг, а в трубе цилиндр. И, как сказал поэт, «школьные науки дадутся сами в руки».
Книгу можно скачать и распечатать, но лучше конечно приобрести оригинал.

Купить книгу «Веселая геометрия для самых маленьких» можно в интернет-магазине «Лабиринт» —

Методика обучения математике. Методика обучения математике Работа по разъяснению текста задачи

Целью данного курса является формирование математических ЗУН и общее развитие учащихся. Концепция курса- целенаправленное развитие мышления всех учащихся в процессе усвоения программного содержания. Курс построен по тематическому принципу и сориентирован на усвоение системы понятий и общих способов действий. При этом повторение ранее изученных вопросов органически включается во все этапы усвоения нового содержания.

Организация такого продуктивного повторения обеспечивает преемственность между темами и создает условия для активного использования приемов умственной деятельности в процессе усвоения математического содержания. Таким образом, на методическом уровне реализуется психолого-педагогические идеи развивающего обучения.

В программе Истоминой изменена последовательность изучения некоторых вопросов программы, по сравнению с программой Моро. Значительно усилена геометрическая линия и предусматривается использование калькуляторов при выполнении ряда заданий.

Суть данной концепции связана с определенными ответами на 3 основных вопроса методической науки:

1. зачем учить?

2.чему учить?

3.как учить?

Ответ на 1-ый вопрос «зачем учить?» нашел отражение в направленности курса в начальной математике на формирование у школьников приемов умственной деятельности (анализ, синтез, обобщение, классификация и т.д), которые в процессе обучения математике выполняют различные функции и их можно рассматривать:

1.как способы организации учебной деятельности учащихся

2.как способы познания, которые становятся достояние ребенка, характеризуя его интеллектуальный потенциал и способности к усвоению знания

3.как способы включения в познание различных психических процессов: эмоции, воли, чувств и внимания.

В результате интеллектуальная деятельность ребенка входит в различные соотношения с другими сторонами его личности, прежде всего, с ее направленностью, мотивацией, интересами, уровнем притязаний, т.е. характеризуется возрастающей активностью личности в различных сферах ее деятельности.

Вопрос «Как учить?» является основным в концепции курса. Ответ на него требует прежде всего принятия определенной позиции в отношении процесса усвоения детьми знаний, формирования умений и навыков. В зависимости от ответа на этот вопрос, можно выделить 2 позиции:

В одном случае знания и способы действий предлагаются ученикам в виде известного учителю образца, который дети должны запомнить и воспроизвести. Затем путем тренировочных упражнений «отработать их».

В другом случае ученик сначала включается в деятельность, у него возникает потребность в усвоении новых знаний, ион сам добывает их под руководством учителя.

Вторая позиция, по мнению психологов, является более эффективной для развития мышления, но она требует внесения существенных изменений в организацию учебной деятельности школьников. Именно эти изменения и обусловили необходимость создания учебников, в которых нашли отражение:

1.новая логика построения содержания курса, в основе которой лежит тематический принцип, позволяющий сориентировать курс на усвоение систему понятий и общих способов действий.

2.новые методические подходы к усвоению школьниками математических понятий, в основе которых лежат установленные соответствия между предметными вербальными, графическими, схематическими и символическими моделями, а также формирование у них общих представлений об изменении правил и зависимости, что является основой не только для изучения математики, но для закономерности и зависимости окружающего мира.

3.Новая система учебных заданий, которая адекватна концепции курса логики построения его содержания и нацелена на осознание школьниками учебных задач, на овладение способами их решения и на формирование умения контролировать и оценивать свои действия.

4.Новый методический подход к обучению решению задач, который сориентирован на формирование обобщенных изменений: читать задачу, выделять условие и вопрос, устанавливать взаимосвязь между ними и, используя математические понятия, осуществлять переход вербальной модели в символическую.

5.Активное использование приемов умственной деятельности при формировании геометрических представлений, нацеленность на развитие пространственного мышления школьников и умение устанавливать соответствия между моделями геометрических фигур, их изображением и разверткой. Наряду с этим учащиеся овладевают навыком работы с линейкой, циркулем и угольником.

6.Методика использования калькулятора, который рассматривается, как средство обучения младших школьников математике, обладающими определенными методическими возможностями.

7.Организация дифференцируемого обучения.

8.Диалоги Маши и Миша, которые помогают научить младших школьников анализировать предложенную информацию, осуждать ее, высказывать и обосновывать свою точку зрения.

Тетрадь с печатной основой «Учимся решать задачи. 1 класс» содержит дополнительный материал к учебнику «Математика. 1 класс» для четырехлетней начальной школы (автор Н. Б. Истомина). В ней представлены задания, в процессе выполнения которых ученики овладевают навыками чтения и различными видами учебной деятельности, необходимыми для самостоятельного и осознанного решения арифметических задач. Задания направлены на формирование универсальных учебных действий, что соответствует требованиям Федерального государственного образовательного стандарта начального общего образования.

Фрагмент из книги:
Закрась у каждого ребёнка шарик в правой руке зелёным цветом, а в левой руке — красным.
Катя (К), Миша (М), Лена (Л) и Таня (Т) сидят за столом. Катя справа от Миши, а Лена — слева от Миши.

Скачать и читать Наглядная геометрия, Тетрадь по математике, 1 класс, Истомина Н.Б., Редько З.Б., 2016

10. Обведи линией пару фигур, у которых:
1) одинаковая форма;
2) разная форма.

Карточки с математическими заданиями составлены в дополнение к учебнику «Математика. 2 класс» (автор — профессор Н. Б. Истомина), но могут быть использованы и при работе по другим учебникам. Пособие включает задания по основным темам курса математики, изучаемым во втором классе: «Двузначные числа. Сложение и вычитание»; «Умножение». Разделы, посвященные проверке вычислительных навыков, включают в себя карточки-перфокарты. Для многоразового использования их целесообразно наклеить на плотную бумагу, а затем вырезать отмеченные прямоугольники. Накладывая карточку на клетчатый лист бумаги, ученик будет записывать в «окошки» только нужные числа или знаки, что очень удобно для проверки знаний.

Скачать и читать Дидактические карточки-задания по математике, 2 класс, Истомина Н.Б., Шмырева Г.Г., 2002

Тетрадь с печатной основой содержит дополнительный материал к учебникам «Математика. 1 класс» и «Математика. 2 класс» (автор профессор Н. Б. Истомина). Выполнение заданий, предложенных в тетради, способствует формированию у учащихся приёмов умственной деятельности (анализ, синтез, сравнение), развивает такие качества мышления, как гибкость и критичность, расширяет представление младших школьников о способах моделирования при решении текстовых задач.
Тетрадь можно использовать, работая с детьми и по другим учебникам математики для начальных классов, а также в прогимназиях и при подготовке детей к школе.

Развивающее обучение

Рекомендовано УМО по специальностям педагогического образования в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 031200(050708)- педагогика и методика начального образования.

1НИСЕЙСКОВ Педучилищ*1 Смоленск «Ассоциация XXI век»

Истомина Н. Б.

И89 Методика обучения математике в начальной школе:

Развивающее обучение. — Смоленск: Изд-во «Ассоциация XXI век», 2005. — 2 7 2 с.

Цель учебного пособия — формирование у будущего учителя методических знаний, умений и опыта творческой деятельности для реализации на практике идей развивающего обучения младших школьников математике.

Пособие будет полезно также учителям, работающим в начальных классах.

ISBN 5-89308-193-5 © Истомина Н. В., 2005 ISBN 5-89308-193-5 © Ассоциация XXI век, 2005

ВВЕДЕНИЕ

В соответствии с государственным стандартом начального общего образовая изучение математики на начальной ступени направлено на достижение следудих целей:

Развитие образного и логического мышления, воображения, формирование ~эедметных умений и навыков, необходимых для успешного решения учебных и ~Фактических задач, продолжения образования;

Освоение основ математических знаний, формирование первоначальных ~эедставлений о математике;

Воспитание интереса к математике, стремление использовать математические знания в повседневной жизни 1.

Задача практической реализации этих целей возлагается на учителя и во мноом зависит от его методической подготовки, которая должна интегрировать в себе:~ециальные (математические), психолого-педагогические и методические знания, умения и навыки.

Данное пособие предназначено для студентов дневного отделения факультета начальных классов и для учащихся педагогических училищ и колледжей, так как, «эиступая к изучению курса «Методика обучения математике», они находятся в равчых условиях с точки зрения опыта методической деятельности и в равной степени должны быть готовы к решению тех задач, которые у них возникнут в процессе практической работы.

Первая глава призвана сформировать у будущего учителя представления о методике обучения математике как педагогической науке (§1), о развитии начального математического образования (§2), о методической деятельности учителя в процессе обучения младших школьников математике (§3).

Во второй главе дается методическая интерпретация основных компонентов понятия «учебная деятельность» и способов ее организации. ).

Эти приемы в процессе усвоения знаний, умений и навыков выполняют различные функции. Их можно рассматривать:

1) как способы организации учебной деятельности школьников;

2) как способы познания, которые становятся достоянием ребенка, характеризуя его интеллектуальный потенциал и способности к усвоению знаний, умений и навыков;

«Федеральный компонент государственного стандарта общего образования. — М., 2004 — С.

3) как способы включения в процесс познания различных психических функций:

эмоций, воли, чувств, внимания, памяти. В результате интеллектуальная деятельность ребенка входит в различные соотношения с другими сторонами его личности, прежде всего с направленностью, мотивацией, интересами, уровнем притязаний, т.е. характеризуется возрастающей активностью личности.

В этой же главе описываются различные способы обоснования истинности суждений младшими школьниками (индуктивные и дедуктивные рассуждения, эксперимент, вычисления, измерения (§2), а также взаимосвязь логического и алгоритмического мышления (§3).

В процессе изучения методического курса будущему учителю необходимо овладеть умением ориентироваться в предметном содержании методической деятельности, т. е. научиться отвечать на вопросы:

Какие математические понятия, законы, свойства и способы действий нашли отражение в начальном курсе математики?

В каком виде они предлагаются младшим школьникам?

В какой последовательности они изучаются?

В какой последовательности могут изучаться?

Формирование этого умения осуществляется в процессе изучения главы 4 «Основные понятия начального курса математики и особенности их усвоения младшими школьниками». Ее содержание включает теоретические сведения о различных понятиях начального курса математики; виды учебных заданий, в процессе выполнения которых дети не только овладевают знаниями, умениями и навыками, но и продвигаются в своем развитии; методические рекомендации к организации учебной деятельности учащихся.

Установление соответствия между предметными, вербальными, схематическими и символическими моделями рассматривается как основной способ усвоения учащимися математических понятий. Он позволяет учитывать индивидуальные особенности ребенка, его жизненный опыт, предметно-действенное и нагляднообразное мышление и постепенно вводить его в мир математических понятий, терминов, символов, т.е. в мир математических знаний, способствуя тем самым развитию как эмпирического, так и теоретического мышления.

Глава 5 посвящена методике организации вычислительной деятельности младших школьников в развивающем курсе начальной математики.

В главе 6 дается краткая характеристика различных методических подходов к обучению младших школьников решению текстовых задач и подробно раскрывается методика формирования обобщенных умений решения задач, в основе которой лежат различные методические приемы: выбор схемы, выражений, условия, переформулировка вопроса задачи, постановка вопросов к данному условию и др.

В главе 7 дается характеристика различных подходов к построению урока математики в начальных классах и рекомендации к планированию и анализу развивающих уроков.

включить маленького школьника в активную познавательную деятельность, н^равленную на усвоение системы математических понятий и общих способов ействий;

Создать методические условия для формирования учебной деятельности, для азвития эмпирического и теоретического мышления, эмоций и чувств ребенка;

Сформировать умение общаться в процессе обсуждения способов решения гзличных задач, обосновывать свои действия и критически оценивать их;

Повысить качество усвоения математических знаний, умений и навыков;

Обеспечить преемственность между начальным и средним звеном обучения, эдготовив учащихся начальных классов к активной мыслительной деятельности;

Развить творческий методический потенциал учителя начальных классов, стиулируя его к самостоятельному составлению учебных заданий, выбору средств и орм организации деятельности школьников.

Начальная школа работает по учебникам Н.Б. Истоминой с 1993 года. Они вклюны в Федеральный Перечень учебников и имеют гриф «Рекомендовано Министергвом общего и профессионального образования Российской Федерации».

За создание учебно-методического комплекта по математике для четырехлетэй начальной школы доктор педагогических наук, профессор Истомина Наталия орисовна в 1999 году удостоена премии Правительства Российской Федерации.

МЕТОДИКА ОБУЧЕНИЯ МАТЕМАТИКЕ

В НАЧАЛЬНЫХ КЛАССАХ КАК ПЕДАГОГИЧЕСКАЯ НАУКА

И КАК УЧЕБНЫЙ ПРЕДМЕТ

§ 1. НАУКА ОБ ОБУЧЕНИИ МАТЕМАТИКЕ

Обучение — это целенаправленная, специально организованная и управляемая учителем деятельность учащихся, в ходе которой они усваивают знания, развиваются и воспитываются.

В обучении, как и в любом процессе, проявляются определенные закономерности, которые выражают существующие связи между педагогическими явлениями, при этом изменение одних явлений влечет за собой изменение других. Например, цели обучения, отражающие потребности общества, оказывают влияние на содержание и на способы организации деятельности учащихся, направленной на его усвоение. Результаты обучения зависят от характера деятельности, в которую на том или ином этапе развития включается ученик. Если приоритет отдается, например, репродуктивной деятельности, то остается невостребованным личностный потенциал школьников, их творческое отношение к учению, самостоятельность мышления.

Экспериментально доказано, что творчество детей находится в прямой зависимости от творчества педагогов, которые вовлекают учащихся в процесс совместного решения различных учебных задач.

Стратегию обучения определяют дидактические принципы. Но они носят общий характер и не учитывают специфики тех проблем, которые возникают при обучении математике. Взятые в абстрактном виде, в отрыве от математической сути, они не могут непосредственно служить теоретическими основами методики, так как остается неясным, как же, опираясь на них, выстраивать обучение конкретному содержанию.

Например, в дидактике разработана теория проблемного обучения: определена сущность ее основных понятий, обоснована необходимость и эффективность их применения в учебном процессе, раскрыт ряд способов организации и управления самостоятельной деятельностью учащихся, выявлены важнейшие дидактические условия реализации такого типа обучения. Однако решение вопроса о возможности создания проблемных ситуаций при обучении младших школьников математике остается за методикой. И пока он не будет представлен на методическом уровне, теория проблемного обучения, получившая разработку в дидактике, не станет достоянием практики работы учителей начальных классов.

Задачей методики обучения математике является не только разработка проблемных ситуаций, но и общих подходов к их использованию, в которых бы учитывалась специфика математического содержания и особенности его усвоения учащимися. Так, например, одним из средств создания проблемных ситуаций на определенном этапе обучения математике являются нестандартные задачи. Они представляют для ученика проблему, способ решения которой он должен найти самостоятельно, творчески применив имеющиеся у него знания. Но в то же время такого рода проблемные ситуации могут оказаться недоступными для большинства младших школьников, так как их решение требует высокого уровня абстракции и обобщения.

Учитывая этот факт, в начальном курсе математики для создания проблемных ситуаций целесообразно использовать задачи практического характера, при решении которых дети могут опираться на свой жизненный опыт и на практические действия.

Так, приступая к изучению темы «Длина предметов» (1-й класс) учитель предлагает классу две полоски (красную и синюю) и спрашивает: «Как можно определить, какая из них длиннее?» Для младшего школьника это проблемная ситуация, способ решения которой ему предложено найти самостоятельно.

Доступность в данном случае обеспечивается тем, что при нахождении способа сравнения длин полосок он может опираться только на свой жизненный опыт и на практические действия. Эту проблемную ситуацию можно усложнить, предложив вопрос: «Можно ли сравнить длины данных полосок с помощью третьей?» Ответ на него связан с нахождением нового способа действия, который лежит в основе измерения величин.

Аналогично можно проиллюстрировать и другие положения дидактики, которые становятся теоретическими основами методики обучения математике только после переработки их в связи с конкретным содержанием изучаемого математического материала.

Например, принцип доступности обучения в дидактике понимается как требование представить учащимся материал такой сложности, которую они могли бы самостоятельно или с помощью учителя преодолеть. Но как это сделать, допустим, при изучении деления многозначного числа на однозначное? Ответ может дать только методика обучения математике. Руководствуясь алгоритмом письменного деления и принципом построения десятичной системы счисления, а также учитывая психологические особенности восприятия и мышления младших школьников, методика начального обучения математике формулирует общие положения, которыми учитель может руководствоваться при формировании у детей навыков письменного деления. Например: знакомству учащихся с алгоритмом письменного деления должны предшествовать упражнения, которые подготовят их к восприятию и пониманию операций, входящих в данный алгоритм. Это и определение количества десятков, сотен, тысяч в многозначном числе, и выполнение деления с остатком, и проверка деления умножением и т.д. Руководство этим методическим положением обеспечивает доступность нового способа действия и дает простор большей самостоятельности учащихся в его усвоении.

При изучении алгоритма письменного деления следует иметь в виду и такое положение: при выполнении записи письменного деления необходимо подробно (развернуто) комментировать производимые операции, так как это позволит учителю не только контролировать правильность конечного результата, но и процесса его вычисления, и тем самым своевременно корректировать деятельность учащихся по использованию алгоритма.

В приведенной методической рекомендации учитывается одна из психологических закономерностей, состоящая в том, что внешняя деятельность не всегда совпадает с внутренней. Это означает, что внешне дети могут выполнять правильные действия, а в уме в это время рассуждать неверно. Таким образом, рекомендация об использовании приема комментирования является обобщенной (в данном случае по отношению к изучению определенного вопроса), теоретически обоснованной (психологическим положением), и может быть применена при изучении других вопросов содержания. Ее целесообразность подтверждается практикой обучения.

Нельзя не учитывать, что особенность использования теоретических положений дидактики при обучении конкретному предмету заключается в том, что они становятся действенными, только вступая во взаимосвязь с психологическими закономерностями, которые, так же как и дидактические, обычно высказываются обобщенно, в отрыве от конкретного содержания.

Итак, процесс усвоения детьми различного содержания, подчиняясь общим закономерностям, имеет свою специфику, которая должна найти выражение в теоретических положениях, отражающих особенности обучения конкретному предмету.

Разработка теории обучения с учетом специфики содержания и есть необходимое условие успешного развития определенного раздела методики преподавания конкретной учебной дисциплины.

Каким же требованиям должны отвечать теоретические основы методики обучения математике? Они должны: а) опираться на определенную теорию (психологическую, педагогическую, математическую), используя ее применительно к конкретному содержанию обучения; б) являться обобщенными положениями, отражающими не отдельный случай, а общие подходы к процессу обучения математике (в частности, в начальных классах), к решению некоторой совокупности вопросов в нем; в) отражать устойчивые особенности процесса обучения математике, т. е. закономерности этого процесса или важные факты о нем; г) подтверждаться на практике экспериментами или опытом работы учителей.

Следовательно, теоретические основы методики обучения математике — это система положений, лежащих в основе построения процесса обучения математике, которые теоретически обосновываются и характеризуют общие методические подходы к его организации.

Рассматривая методику обучения математике в начальных классах как науку, выделим круг проблем, которые она призвана решать, и определим объект и предмет ее исследования.

Все многообразие проблем частных методик, в том числе и методики обучения математике в начальных классах, можно сформулировать в виде вопросов:

Зачем обучать? То есть с какой целью обучать детей математике?

Чему обучать? То есть каким должно быть содержание математического образования в соответствии с поставленными целями?

Как обучать? То есть:

а) в какой последовательности расположить вопросы содержания, чтобы учащиеся могли сознательно усваивать их, эффективно продвигаясь в своем развитии;

б) какие способы организации деятельности учеников (методы, приемы, средва и формы обучения) следует применять для этого;

в) как обучать детей с учетом их психологических особенностей (как в процессе нения математике наиболее полно и правильно использовать закономерности z: зприятия, памяти, мышления, внимания младших школьников)?

Названные проблемы позволяют определить методику обучения математике ак науку, которая, с одной стороны, обращена к конкретному содержанию, отбои упорядочению его в соответствии с поставленными целями обучения, с другой — к человеческой деятельности (учителя и ученика), к процессу усвоения этого держания, управление которым осуществляет учитель.

Объект исследования методики обучения математике — процесс обучения математике, в котором можно выделить четыре основных компонента: цель, содержаj, деятельность учителя и деятельность учащихся. Перечисленные компоненты

2ХОДЯТСЯ во взаимосвязи и взаимообусловленности, т. е. образуют систему, в которой изменение одного из компонентов вызывает изменения других.

Предметом исследования может являться каждый из компонентов этой системы, а также те взаимосвязи и отношения, которые существуют между ними.

Методические проблемы решаются с помощью методов педагогических исследований, к которым относятся: наблюдение, беседа, анкетирование, обобщение передового опыта работы учителей, лабораторный и естественный эксперименты.

Различные тесты и психологические методики дают возможность выявить влияние эазных способов обучения на усвоение знаний, умений и навыков, на общее развитие детей. Все это позволяет установить определенные закономерности процесса обучения математике.

Задание 1. С какими концепциями обучения младших школьников вы знакомы? Раскройте содержание этих концепций.

§ 2. ОБЩАЯ ХАРАКТЕРИСТИКА РАЗВИТИЯ НАЧАЛЬНОГО

МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ

На каждом этапе развития начального образования методическая наука поразному отвечала на вопросы: «Зачем учить?», «Чему учить?», «Как учить?»

До 1949 г. приоритетом в начальном образовании были практические цели. Это обусловливалось тем, что до введения общего обязательного 7-летнего образования начальная школа представляла замкнутый этап. Основным содержанием начального курса математики являлось изучение четырех арифметических действий, решение задач арифметическим способом и знакомство с геометрическим материалом, который был подчинен решению практических задач (размечать земельные участки прямоугольной формы, измерять их длину, ширину, вычислять по формулам площадь и периметр прямоугольника и др.).

В основу построения содержания курса был положен концентрический принцип (5-6 концентров). В конце четвертого года обучения предполагалось обобщение изученного материала и ознакомление с отдельными элементами теории (связи между действиями, компонентами и результатами действий, некоторые свойства действий).

Методы обучения учитывали те особенности данного возраста, которые отмечала психологическая наука: образность, преобладание «механической» памяти над смысловой, легкость и прочность усвоения младшими школьниками многочисленных фактов.

В расчете на «механическую» память детям предписывалось запомнить 4 таблицы (2 таблицы умножения и 2 таблицы деления, каждая из которых включала по 100 примеров). Такой подход к обучению математике в начальных классах обосновывался данными возрастной психологии, которая учет реальных познавательных возможностей младших школьников трактовала как необходимость приспособления содержания и методов обучения к особенностям психического развития детей данного возраста.

Однако, в работах Л. С. Выготского, виднейшего отечественного психолога, еще в начале 30-х годов XX века отмечалась ошибочность этой позиции, даже по отношению к детям, которые отставали в умственном развитии. Он отмечал, что обучение, которое ориентируется на уже завершенные циклы развития, не ведет за собой процесс развития, а само плетется у него в хвосте; только то обучение является хорошим, которое забегает вперед развития.

Следует отметить, что 30-40 годы знаменуются совместными исследованиями психологов и методистов по вопросам методики преподавания отдельных предметов. По поводу направлений этих исследований психолог Н. А. Менчинская писала:

«Для того чтобы психология могла прямо ответить на запросы практики обучения, необходимо подвергать изучению конкретные виды учебной деятельности, причем исследовать различные формы этой деятельности как закономерный ответ на педагогические воздействия»1.

В русле этого направления изучались пути усвоения детьми понятия числа и арифметических действий, особенности овладения процессом счета и формирования вычислительных навыков, умение решать текстовые арифметические задачи.

При этом большое внимание уделялось изучению роли анализа и синтеза, конкретизации, абстрагирования и обобщений. Результаты этих исследований сыграли определенную роль в развитии методической науки.

Говоря о недостатках методики обучения математике, А. С. Пчелко (автор учебника арифметики для начальных классов) сетовал на то, что основное внимание методистов сосредоточено на учителе, на методах и приемах, которыми он обучает детей, и совсем не освещаются вопросы о том, как учащиеся воспринимают объяснения учителя, какие затруднения возникают у них при усвоении того или иного раздела арифметики, в чем причина этих затруднений и как их можно предупредить.

В 40-50 годы появляются методические работы, построенные на исследовательском, экспериментальном материале (Н. Н. Никитин, Г. Б. Поляк, М. Н. Скаткин,

Менчинская Н. А. Психология обучения арифметике. — М., 1947.

А. С. Пчелко) и возникает необходимость в пересмотре содержания обучения в начальных классах.

Однако изменения, внесенные в программу курса арифметики, которая была зведена в 1960 г., не коснулись ее сущности. Они сводились к незначительным поправкам, направленным в основном на дальнейшее упрощение курса. Новые веяния, вызванные к жизни исследованиями в области методики и психологии, нашли отражение только в объяснительной записке программы. В ней подчеркивалась необходимость обучения младших школьников общим приемам работы над задачей, важность формирования у детей правильных обобщений и организации различных зидов самостоятельной работы.

В 1965 г. выходит книга М. И. Моро и Н. А. Менчинской «Вопросы методики и психологии обучения арифметике…». Целый ряд положений, сформулированных в этой книге, остаются актуальными и сегодня, являясь основой для разработки новых методических подходов к усвоению младшими школьниками математического содержания. Приведем некоторые из них1.

«Для того чтобы младший школьник был активным в процессе обучения, необходимо: во-первых, обеспечить ему широкую возможность для проявления самостоятельности в учебной работе; во-вторых, научить его приемам и методам самостоятельной работы; в-третьих, пробудить в нем стремление к самостоятельности, создав у него соответствующую мотивацию, т. е. сделать для него самого жизненно важным его самостоятельный творческий подход к решению учебных задач».

«Широко известная старинная поговорка гласит: «Повторение — мать учения».

Теперь иногда ей противопоставляется другая: «Применение — мать учения». Вторая формулировка больше отвечает современным задачам, стоящим перед нашей школой, но надо иметь в виду, что применение знаний не исключает повторения, а включает его в себя, но при этом имеется в виду повторение не однообразное или монотонное, а такое, которое предполагает изменение как самих знаний, так и условий их использования».

«Умение решать задачи, хотя оно и носит общий характер, поддается развитию, как и все другие, но для этого нужна особая система упражнений, направленная на то, чтобы формировать у школьников потребность в творческом мышлении, интерес к самостоятельному решению задач-проблем, а следовательно, и к поиску наиболее рациональных приемов их решения».

«Полная сознательность усвоения может быть достигнута учеником только при условии, если он не пассивно воспринимает сообщаемый новый материал, а активно оперирует им».

«Следует избегать не только чрезвычайно трудного, но и чрезвычайно легкого для усвоения учеником материала, когда в процессе усвоения для него не возникает никаких проблем или задач, требующих умственных усилий».

Менчинская Н. А., Моро М. И. Вопросы методики и психологии обучения арифметике в начальных классах. — М., 1965.

В книге не только отмечена роль сравнений и противопоставлений как смешиваемых детьми понятий, но и предложены основные пути их применения в процессе обучения математике. Это одновременное противопоставление, когда оба понятия или правила вводятся на одном уроке, в сопоставлении друг с другом, и последовательное, когда сначала изучается одно из сравниваемых понятий, а второе вводится на основе противопоставления первому, только когда первое уже усвоено.

Большой вклад в развитие методики обучения математике внесли работы П. М. Эрдниева. Под его руководством было проведено экспериментальное исследование с целью обоснования идеи укрупнения дидактических единиц в процессе обучения детей математике (метод УДЕ).

Обучение, построенное в соответствии с этой идеей, оказывается эффективным для повышения качества знаний учащихся при значительной экономии времени, расходуемого на изучение курса математики.

а) одновременное изучение сходных понятий; б) одновременное изучение взаимно обратных действий; в) преобразование математических упражнений; г) составление задач школьниками; д) деформированные примеры.

В числе исследований, которые сыграли неоценимую роль в развитии методики начального обучения, следует назвать два: одно под руководством Л. В. Занкова (1957 г.), другое — под руководством Д. Б. Эльконина и В. В. Давыдова (1959 г.).

И хотя объектом экспериментального исследования Л. В. Занкова являлись не отдельные учебные предметы, а дидактическая система, охватывающая все начальное обучение, тем не менее разработанные в лаборатории дидактические принципы (обучение на высоком уровне трудности, изучение программного материала быстрым темпом; ведущая роль теоретических знаний; осознание школьниками процесса учения; целенаправленная и систематическая работа над развитием всех учащихся класса, в том числе и наиболее слабых) могли служить действенной основой для совершенствования методики обучения математике.

Широкомасштабный эксперимент, проведенный под руководством Л. В. Занкова, привел к теоретическому осмыслению типических свойств методической системы начального обучения. В качестве таких свойств ученый называл многогранность, коллизии, процессуальность. Разработку методической системы Л. В. Занков считал особенно актуальной.

В исследовании под руководством Д. Б. Эльконина и В. В. Давыдова были выделены те новообразования, формирование которых у учащихся начальных классов оказалось возможным при определенном построении процесса обучения. В качестве таких новообразований были названы: учебная деятельность, теоретическое мышление и произвольное управление поведением (рефлексия).

Параллельно с психолого-педагогическими проводились исследования методического характера, нацеленные на подготовку реформы начального образования. Разрабатывались варианты программ, создавались экспериментальные учебники.

Огромный вклад в подготовку реформы математического образования на этом этапе внесли ученые-методисты М. И. Моро, А. С. Пчелко, М. А. Бантова, Г. В. Бельтюкова, Н. В. Меленцова, Е. М. Семенов, П. М. Эрдниев, И. К. Андронов, Ю. М. Коляг ин. В подготовке реформы начального образования активно участвовали психологи (Н. А. Менчинская, А. А. Люблинская).

В результате проведенных исследований были сделаны выводы о необходимости обогащения содержания начального курса математики, усиления в нем роли теории и включения в содержание курса элементов алгебры и геометрии.

Модернизация предметного содержания начального математического образозания сопровождалась указаниями: «Одна из важных воспитательных задач, связанных с изучением курса математики, — развитие познавательных способностей учащихся»; «Занятия математикой должны способствовать воспитанию у детей самостоятельности, инициативы, творчества, культуры труда»; «Обучение и развитие при изучении математического материала должны осуществляться в неразрывной связи друг с другом»1.

Однако реализация этих указаний в школьной практике оказалась, пожалуй, еще более сложной задачей, нежели внедрение нового содержания единого наального курса математики. «Учителя получили новые программы и приступили к их:существлению, понятия не имея о новой методике», — пишет Ш. А. Амонашвили.

Задача развития ребенка в процессе обучения так и осталась нерешенной в стабильном курсе математики (М. И. Моро и др.)- Несмотря на его содержательное обобщение по сравнению с курсом арифметики и нацеленностью на повышение уровня теоретических знаний младших школьников, ведущим методом оставался показ обзазца и его закрепление. Учебные задания были однообразны, а задания, требующие активизации мыслительной деятельности школьников, классифицировались как материал «повышенной трудности» и «доставались» только способным к математике летям. Основной же задачей для всех учащихся по-прежнему оставалось формирозание вычислительных умений, навыков и умение решать определенные типы задач.

Между тем поиски способов организации учебной деятельности младших школьников продолжались как в теории, так и практике обучения.

В 70-80-е годы тысячи школьников работали по системе Л. В. Занкова, продолжался эксперимент по системе Д. Б. Эльконина, В. В. Давыдова, активно внедрялась в школьную практику система УДЕ, проводился эксперимент А. М. Пышкало и К. И. Нешкова, в котором проверялась возможность построения начального курса математики на теоретико-множественной основе.

Актуальные проблемы методики обучения математике в начальных классах/Под ред. М. И. Моро, А. М. Пышкало. — М., 1977.

Амонашвили Ш. А. в сб. статей «Новое время — новая дидактика»: Педагогические идеи Л. В. Занкова и школьная практика. — Москва — Самара, 2000.

Начало 90-х годов знаменуется внедрением в школьную практику различных инноваций, новых технологий обучения, вариативных авторских программ и учебников.

На волне этого инновационного движения «российское начальное образование приобретает развивающий характер»1.

На передний план выдвигаются задачи становления у ребенка интереса к учению, формирования учебной самостоятельности и необходимых для нее умений, связанных с осознанием учебной задачи, с поиском ее решения, с выполнением различных мыслительных операций (анализа, синтеза, сравнения, классификации, обобщения), с организацией контроля за своими действиями и их оценкой.

Осмысление этих направлений на методическом уровне — актуальная задача современной методической науки.

§ 3. ЗАДАЧИ МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ

КАК УЧЕБНОГО ПРЕДМЕТА

Основная задача курса «Методика обучения математике в начальных классах» в колледже и в вузе — подготовить студентов к профессиональной методической деятельности, направленной на воспитание личности ребенка, на развитие его мышления, на формирование у него умения и желания учиться, на приобретение опыта общения и сотрудничества в процессе усвоения математического содержания.

Определенный вклад в решение этой задачи вносят курсы математики, психологии, возрастной психологии, дидактики и др. В процессе изучения методического курса студенты учатся применять эти знания для решения методических задач. Следовательно, методическая деятельность учителя носит интегративный характер.

Сложный механизм такой интеграции обусловлен тем, что методические знания, представленные в виде идей, положений, описаний рекомендаций, приемов, видов учебных заданий, включают в себя:

Закономерности процессов обучения и воспитания;

Психологические особенности развития ребенка и усвоения им знаний, умений и навыков.

Чем лучше учитель осознает эту связь, тем выше уровень его методической подготовки, тем шире его возможности в осуществлении творческой методической деятельности.

Рассмотрим типичную ситуацию из практики начального обучения математике и проанализируем ее сточки зрения понятия «методическая задача».

Представьте, что вы предложили детям задание: «Сравни числа 6 и 8» или «Поставь между числами 6 и 8 знак, = так, чтобы получилась верная запись». Предположим, что ученик дал неверный ответ, т. е. выполнил запись 68. Как вы поступите? Обратитесь к другому ученику или попытаетесь разобраться в причинах допущенной ошибки? Другими словами, как вы решите эту методическую задачу?

«Давыдов В. В. Концепция гуманизации российского начального образования. — Сб. «Начальное образование в России». — М., 1994.

Выбор методических действий в этом случае может быть обусловлен целым ряZOM психолого-педагогических факторов: личностью ученика, уровнем его математиеской подготовки, целью, с которой предлагалось данное задание, и т. д. Допустим, в выбрали второй путь, т. е. решили попытаться разобраться в причинах ошибки. Но = в это сделать?

Если ученик читает ее как «шесть меньше восьми», значит, причина ошибки в «: и, что не усвоен математический символ. Дети одновременно знакомятся со знаи и, поэтому они могут путать их значения.

Установив таким образом причину, можно продолжить работу. Но при этом

Ркно учитывать особенности восприятия младшего школьника. Так как оно имеет

Аглядно-образный характер, то учитель использует прием сравнения знака с конэетным (для ребенка) образом, например, с клювиком, который раскрыт к больему числу и закрыт к меньшему (5 8, 8 5). Такое сравнение поможет ребенку запомнить математическую символику.

Но если ученик прочитал данную запись «6 8» как «шесть больше восьми», то зшибка обусловлена уже другой причиной. Как поступить в этом случае?

Здесь учителю не обойтись без знания таких математических понятий, как «количественное число», «установление взаимно-однозначного соответствия» и теореико-множественный подход к определению отношения «больше» («меньше»). Это позволит ему правильно выбрать способ организации деятельности учащихся, связанный с выполнением данного задания. Учитывая наглядно-действенный характер мышления младших школьников, учитель предлагает одному ученику выложить на парте 6 предметов, а другому — 8 и подумать, как можно расположить их, чтобы выяснить, у кого больше предметов, а у кого меньше.

Опираясь на свой жизненный опыт, ребенок может самостоятельно предложить способ действий или найти его с помощью учителя, т. е. установить взаимно-однозначное соответствие между элементами данных предметных множеств.

§ §§!§ till id Теперь представим, что ученик успешно справляется с выполнением задания на сравнение чисел. В этом случае важно установить, насколько осознанны его действия, т. е. может ли он обосновать их, высказав при этом необходимые рассуждения, которые связаны с ответом на вопрос: «Почему 6 меньше 8?»

Для решения этой задачи учителю понадобится знание таких математических понятий, как «счет» и «натуральный ряд чисел», т. к. именно они лежат в основе того обоснования, которое может привести учащийся: «Число, которое называется при счете раньше, всегда меньше любого числа, следующего за ним».

Чтобы это обоснование стало понятно всем детям, полезно обратиться к отрезку натурального ряда и предложить подчеркнуть в нем числа 6 и 8 (1, 2, 3, 4, 5, 6, 7, 8, 9) или обозначить данные числа на числовом луче.

Таким образом, процесс выполнения учеником довольно несложного задания потребовал от учителя решения четырех методических задач и применения математических, психологических и методических знаний.

Рассмотрим другую ситуацию, связанную с письменным делением на однозначное число. Например, 8463:7. Каждый из вас, конечно, легко справится с этим заданием.

Но предположим, что ученик получил в ответе не 1209, а 129, т. е. он пропустил в частном нуль (это типичная ошибка). Причиной такой ошибки может быть либо его невнимательность, либо отсутствие необходимых знаний и умений.

Как же это выяснить? Наверное, по аналогии с первой ситуацией вы уже сможете ответить на этот вопрос: «Нужно, чтобы ученик проговорил те действия, которые он выполнял». В методике этот прием носит название «комментирование».

Применение такого приема позволяет учителю проконтролировать правильность не только конечного результата, но и процесса его получения и тем самым скорректировать деятельность школьников по использованию алгоритма.

Но для того, чтобы научить детей осознанно комментировать последовательность операций, которые входят в алгоритм письменного деления, учитель должен сам владеть необходимыми математическими понятиями. При этом условии он сможет доступно разъяснить математическую суть выполняемых операций. Например, для случая 8463:7 появление нуля в частном обычно комментируется так: «6 на 7 не делится — ставим нуль». Это формальное объяснение может быть более обоснованным, если опираться на понятие деления с остатком.

Вспомните определение, которое вы рассматривали в курсе математики: «Разделить с остатком целое неотрицательное число а на натуральное число b значит найти такие целые неотрицательные числа q и г, чтобы a=bq +г\лО r b».

Понимание того, что данное определение является основой действий учащихся при выполнении деления с остатком, позволит учителю методически правильно организовать их деятельность по овладению этими способами. Например, выполняя деление для случая 29:4, ученики сначала находят самое большое число до 29, которое без остатка делится на 4 (эта операция требует прочного усвоения табличных случаев деления): 28:4=7. Остаток находится вычитанием 29-28=1. Конечный результат: 29:4 = 7 (ост. 1).

Перенесем теперь эти же рассуждения на случай 6:7. Самое большое число до 6, которое делится без остатка на 7, это 0. 0:7=0. Находим остаток вычитанием 6-0=6. Конечный результат: 6:7=0 (ост. 6). Так знание математических понятий помогает учителю найти обоснованные способы объяснения учащимся тех действий, которые они выполняют.

Математические знания необходимы учителю для того, чтобы правильно организовать знакомство младших школьников с новыми понятиями. Например, некоорые учителя пытаются объяснить случаи умножения на 1 так: «Число повторили один раз, поэтому оно и осталось». При изучении случая деления на 1 они обращаются к конкретному примеру: «Представьте, что у мальчика 5 яблок. Он оставил их все себе, т. е. разделил их на 1, поэтому и получил 5 яблок». Казалось бы, методические действия педагога учитывают психологические особенности детей, и он стремится обеспечить доступное им введение нового понятия. Тем не менее в его действиях отсутствует та математическая основа, без которой не могут быть сформированы правильные математические представления и понятия.

Ясно, что методические действия учителя при обучении младших школьников математике во многом зависят от уровня его математической подготовки. Помимо этого, математическая подготовка оказывает положительное влияние на четкость оечи учителя, на правильность использования терминологии и обоснованность подбора методических приемов, связанных с изучением математических понятий.

Задание 2. Подумайте, на какие математические знания должен опираться учитель при знакомстве учащихся со случаями умножения и деления на 1.

Деятельность, направленная на воспитание и развитие младшего школьника в процессе обучения математике, требует от педагога овладения не только частными, но и общими методическими умениями. Их можно назвать дидактическими, так как они могут быть использованы учителем не только при обучении математике, но и другим учебным предметам (русский язык, чтение, природоведение и т. д.).

Например, умение целенаправленно применять различные способы организации внимания детей также является компонентом методической деятельности учителя. Основу этих умений составляют его психолого-педагогические знания. Так, отсутствие у учителя психологических знаний об особенностях внимания младших школьников приводит к тому, что, организуя их внимание, он пользуется, как правило, только приемом установки, т. е. говорит: «будьте внимательны». Если же эта установка не действует, он прибегает к различным мерам наказания. Но достаточно разобраться в психологической сути его действий, чтобы понять их ошибочность. А именно: установка «будьте внимательны» рассчитана в основном на произвольное внимание детей. Этот вид внимания требует волевых усилий и быстро их утомляет. Поэтому действенность данной установки очень кратковременна. Пытаясь усилить ее, некоторые учителя, задавая вопрос всему классу, спрашивают именно того ученика, который в данный момент отвлекся. Естественно, он не может ответить. Учитель начинает стыдить его, читать нотацию, наказывать. Но это только увеличивает психическую нагрузку и вызывает у ребенка отрицательные эмоции:

чувство страха, неуверенности, тревожности. Как же избежать этого? Знание психологических закономерностей поможет педагогу найти верное решение.

В психологии, например, установлена такая закономерность: внимание учеников активизируется, если: а) мыслительная деятельность сопровождается моторной; б) объекты, которыми оперирует ученик, воспринимаются зрительно.

Помимо закономерностей, в психологической науке выделены условия, под влиянием которых поддерживается внимание. К ним относятся: а) интенсивность, ЕНИСЕЙСКОМ!

П«дучнляш«

Новизна, неожиданность появления раздражителей и контраст между ними; б) ожидание конкретного события; в) положительные эмоции. Здесь учителю помогут различные методические приемы, реализующие эти закономерности: дидактические игры, связанные с конкретным математическим содержанием, использование предметной наглядности, приемы наблюдения, сравнения, обращение к опыту ребенка, возможность выбора.

Применение различных методических приемов позволяет организовать деятельность учащихся на основе послепроизвольного внимания, т. е. в соответствии с поставленной целью, но без волевых усилий. Это играет большую роль в построении обучения, так как открывает перед учителем перспективу целенаправленного управления вниманием детей.

Но вполне возможно, что могут быть и такие ситуации, когда даже проверенные методические приемы оказываются недостаточными. В этом случае необходимы меры педагогического воздействия. Например, можно обратиться к невнимательному ученику с таким предложением: «А теперь задания для устного счета, которые выписаны на карточках, вам предложит Коля. Он будет контролировать и правильность их решения». В результате Коля включается в работу, испытывая положительные эмоции, вызванные тем доверием, которое оказал ему учитель.

В приведенных примерах учитель решает оперативные методические задачи, т. е. он должен быстро реагировать на те обстоятельства, которые возникают в процессе урока.

Помимо этого методическая деятельность учителя связана с решением проектировочных задач, которые он продумывает при подготовке к уроку, выбирая способ постановки учебной задачи, подбирая учебное задание для ее решения.

Как видите, методическая деятельность учителя связана с решением различных методических задач. Формирование умения выявлять, ставить и решать их — одна из важных задач методического курса.

Задание 3. Приведите примеры методических задач, решение которых вы наблюдали на педагогической практике.

Можете ли вы, используя свои психолого-педагогические и математические знания, предложить другие варианты действий на уроке?

УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ МЛАДШЕГО ШКОЛЬНИКА

В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ

§ 1.

ПОНЯТИЕ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ И ЕЕ СТРУКТУРА

Деятельность — это форма активного отношения человека к окружающей действительности. Она прежде всего характеризуется наличием цели и вызывается эазличными потребностями и интересами (мотивами).

Учебная деятельность направлена непосредственно на усвоение знаний, умений и навыков, ее содержанием являются научные понятия и общие способы решения практических задач. Будучи ведущей для учащихся начальных классов, она стимулирует появление центральных психических новообразований данного возраста, развитие психики и личности школьника. Под возрастными новообразованиями понимается «тот новый тип строения личности и ее деятельности, те психические и социальные изменения, которые впервые возникают на данной ступени и в самом главном и основном определяют сознание ребенка, его отношение к среде, его внутреннюю и внешнюю жизнь, весь ход его развития в данный период»1.

Структура учебной деятельности включает следующие компоненты: мотивы, учебные задачи, способы действий, а также самоконтроль и самооценку. Взаимосвязь этих компонентов обеспечивает целостность учебной деятельности.

Мотив — это побудительная сила деятельности, то, ради чего она осуществляется. Мотивы учебной деятельности динамичны и изменяются в зависимости от социальных установок личности. Вначале они формируются под влиянием внешних по отношению к учебной деятельности факторов, не связанных с ее содержанием.

С помощью мышления учащийся оценивает разные побуждения, сопоставляет их, соотносит с имеющимися у него убеждениями и стремлениями и после эмоциональной оценки этих побуждений приступает к учебным действиям, осознавая их необходимость. Поэтому процесс учения должен быть построен так, чтобы задачи, которые ставятся перед учащимся, были не только понятны, но и внутренне приняты им, чтобы они приобрели для него значимость. Другими словами, необходимо сформировать познавательную мотивацию, тесно связанную с содержанием и способами обучения.

Мотивация (т. е. направленность школьника на учебные действия) чаще всего возникает при постановке учебной задачи. Но в некоторых случаях она может появиться и в процессе самой деятельности, ее контроля и самооценки. Этому обычно способствует успешное выполнение школьником тех учебных заданий, которые учитель предлагает как в процессе решения учебной задачи, так и на этапе самоконтроля.

«Выготский Л. С. Педагогическая психология. — М., 1991.

§ 2. УЧЕБНАЯ ЗАДАЧА И ЕЕ ВИДЫ Учебная задача — ключевой компонент учебной деятельности.

С одной стороны, она уточняет общие цели обучения, конкретизирует познавательные мотивы, с другой — помогает сделать осмысленным сам процесс действий, направленных на ее решение.

В большинстве случаев средством решения учебных задач в математике являются математические задания (упражнения, задачи). Например, овладение алгоритмом письменного умножения составляет учебную задачу, которая решается в процессе выполнения определенной системы учебных заданий (упражнений). Очевидно, что для решения одной учебной задачи может быть использовано несколько, зачастую много математических заданий (упражнений). В то же время в процессе выполнения одного математического задания (упражнения) может решаться несколько учебных задач.

Например:

Даны числа: 18, 81, 881, 42, 442, 818. По какому признаку можно разбить эти числа на две группы?

Похожие работы:

« работников дошкольных учреждений, педагогов общих образовательных учреждений и систем дополнительного образования на основе серии книг «Путешествие на зеленый свет» Москва 2013 || Рабочая программа общего и дополнительного образования детей дошкольного и младшего школьного возраста «Школа юного пешехода» Методическое пособие для работников…»

«Негосударственное образовательное учреждение дополнительного профессионального образования «Экспертно-методический центр» Научно-издательский центр «Articulus-инфо» г. Чебоксары Кафедра литературы ФГБОУ ВПО «Чувашский государственный педагогический университет им. И.Я. Яковлева»НАУКА И ОБРАЗОВАНИЕ: ВЕКТОРЫ РАЗВИТИЯ Материалы I Международной научно-практической конференции 25 ноября 2013 г. Чебоксары УДК 08 ББК 72 + 74 Н 34 Нечаев Михаил Петрович, главный редактор, д.п.н., профессор, Главный…»

«Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уральский государственный педагогический университет» ИНСТИТУТ ИНОСТРАННЫХ ЯЗЫКОВ Ассоциация преподавателей английского языка Уральского региона «ELTA-URALS»ЯЗЫКОВОЕ ОБРАЗОВАНИЕ СЕГОДНЯ – ВЕКТОРЫ РАЗВИТИЯ Материалы III международной научно-практической конференции-форума 20 апреля 2012 года Екатеринбург, Россия Екатеринбург УДК 372.881.1 (063) ББК Ч 426.8 Я 41 к.п.н., доц. Казакова О.П.,…»

«Структура программы государственной итоговой аттестации 1. Место государственной итоговой аттестации в структуре ООП 2. Компетентностная характеристика выпускника аспирантуры 3. Программа государственного экзамена:3.1. Форма проведения государственного экзамена 3.2. Учебно-методическое и информационное обеспечение подготовки к государственному экзамену 3.3. Критерии оценивания ответа аспиранта в ходе Государственного экзамена 4. Методические рекомендации аспирантам по выполнению…»

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВПО «Благовещенский государственный педагогический университет» ОСНОВНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА Рабочая программа дисциплины УТВЕРЖДАЮ Декан естественно-географического факультета ФГБОУ ВПО «БГПУ» _ И.А. Трофимцова «4» июня 2015 г. Рабочая программа дисциплины Б3.Б.4 ОСНОВЫ МЕДИЦИНСКИХ ЗНАНИЙ (с изменениями и дополнениями 2013, 2014, 2015 гг.) Направление подготовки 44.03.05 ПЕДАГОГИЧЕСКОЕ ОБРАЗОВАНИЕ Профиль ГЕОГРАФИЯ Профиль ЭКОЛОГИЯ Квалификация…»

« ГОСУДАРСТВЕННОМ ПЕДАГОГИЧЕСКОМ УНИВЕРСИТЕТЕ им. И.Н.УЛЬЯНОВА ЛУКЬЯНОВА М.И. КАЛИНИНА Н.В.УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ ШКОЛЬНИКОВ: СУЩНОСТЬ И ВОЗМОЖНОСТИ ФОРМИРОВАНИЯ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ УЧИТЕЛЕЙ И ШКОЛЬНЫХ ПСИХОЛОГОВ Ульяновск ББК 88. Л 8 Лукьянова М.И., Калинина Н.В. УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ ШКОЛЬНИКОВ: СУЩНОСТЬ И ВОЗМОЖНОСТИ ФОРМИРОВАНИЯ. Методические…»

«Профилактика употребления курительных смесей детьми и подростками в образовательных учреждениях Методические рекомендации Пенза Авторы-составители: Л. Н. Разуваева, кандидат педагогических наук, доцент кафедры психологии и педагогики ГАОУ ДПО ПИРО; П.Д. Бочаров, кандидат педагогических наук, глава г. Каменка Пензенской области Данные методические рекомендации помогут организовать первичную профилактику употребления курительных смесей обучающимися в образовательных учреждениях, являющуюся частью…»

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тверской государственный университет» Педагогический факультет Кафедра педагогики и психологии начального образования УТВЕРЖДАЮ Декан педагогического факультета _ Т.В. Бабушкина «» 2011 г. УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДПП.Ф.09 МЕТОДИКА ПРЕПОДАВАНИЯ ТЕХНОЛОГИИ С ПРАКТИКУМОМ Для студентов 3,4 курса очной формы обучения 3 курса заочной формы…»

«Государственное образовательное учреждение дополнительного образования (повышения квалификации) специалистов Санкт-Петербургская академия постдипломного педагогического образования Институт общего образования Кафедра педагогики окружающей среды, безопасности и здоровья человека Методические рекомендации ПРОФЕССИОНАЛЬНАЯ ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ ФИЗИЧЕСКОЙ КУЛЬТУРЫ В УСЛОВИЯХ РЕАЛИЗАЦИИ ФГОС Е. В.ПОПОВА, О.В.СТАРОЛАВНИКОВА Санкт-Петербург 2014 г. СОДЕРЖАНИЕ 1.Современные требования к инновационному…»

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Алтайская государственная академия образования имени В.М. Шукшина» (ФГБОУ ВПО «АГАО») Утверждаю Утверждаю: Ректор Начальник МКУ о/: Администрац 220400| «» Согласовано (Протокол № ПредсадаТел Ю. Н. Фролов 2014 г..„S1J //fo ОСНОВНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА ЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Направление подготовки 050100 Педагогическое…»

« педагогический колледж Методические материалы и ФОС по МДК «Теоретические основы начального курса математики с методикой преподавания» Специальность Преподавание в начальных классах Методические материалы и ФОС утверждены на заседании ПЦК социально-гуманитарных дисциплин протокол № 16 от 10.06.2015 Составитель: преподаватель Широкова М.Н….»

«1. Общая характеристика программы подготовки научнопедагогических кадров в аспирантуре по направлению подготовки 09. 06.01 «Информатика и вычислительная техника», профиль подготовки – Математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей. Настоящая основная образовательная программа высшего образования (далее – образовательная программа аспирантуры) по направлению подготовки научно-педагогических кадров в аспирантуре 09.06.0 «Информатика и вычислительная…»

«УДК 373. ББК 74.1 К21 Карабанова О.А., Алиева Э.Ф., Радионова О.Р., Рабинович П.Д., Марич Е.М. Организация развивающей предметно-пространственной К21 среды в соответствии с федеральным государственным образовательным стандартом дошкольного образования. Методические рекомендации для педагогических работников дошкольных образовательных организаций и родителей детей дошкольного возраста / О.А. Карабанова, Э.Ф. Алиева, О.Р. Радионова, П.Д. Рабинович, Е.М. Марич. – М.: Федеральный институт развития…»

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования Ханты-Мансийского автономного округа – Югры «Сургутский государственный педагогический университет» КУРСОВОЕ ИССЛЕДОВАНИЕ Методические рекомендации Направление подготовки 43. 03.02 Туризм Квалификация (степень) бакалавр Сургут 2015 Методические рекомендации утверждены на заседании кафедры социально – гуманитарных дисциплин протокол №10 от 10 июня 2015 г….»

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» ПСИХОЛОГИЯ И ПЕДАГОГИКА Часть 2. Педагогика Методические рекомендации и контрольные работы по дисциплине «Психология и педагогика. Часть 2. Педагогика» для студентов заочного отделения фармацевтического факультета Составители: Е.В. Кривотулова, Н.Ю. Зыкова Издательско-полиграфический центр Воронежского государственного университета…»

«02-33 Муниципальное бюджетное общеобразовательное учреждение « Ведерниковская основная общеобразовательная школа» Обсуждена и принята УТВЕРЖДАЮ на педагогическом совете директор МБОУ « Ведерниковская ООШ» МБОУ «Ведерниковская ООШ» Т.А. Антоненко протокол №1 от 29.08.2012г. приказ №78 от 31. 08.2012 г. Образовательная программа на 2012-2013 год 2012 г. Содержание Введение.. 1. Анализ потенциала развития школы. 2. Анализ актуального уровня развития школы в динамике за три года. 3 3….»

«Муниципальное бюджетное общеобразовательное учреждение городского округа Тольятти «Школа №75 имени И.А. Красюка» Рассмотрено на заседании МО Согласовано на Утверждаю Протокол № 1 от 27.08.2015 г. Педагогическом совете Директор МБУ «Школа №75» Протокол № 1 от 28.08.2015 г. С.А.Гервасьева (Приказ № 597 от 01.09.2015г.) РАБОЧАЯ ПРОГРАММА ПО ГЕОГРАФИИ для 5-9 классов Составили: Юропова Л.В. Мораш О.И. Первая квалификационная категория Тольятти 2015-2016 уч. г. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая…»

«азастан Республикасы Білім жне ылым министрлігі Ы. Алтынсарин атындаы лтты білім академиясы Министерство образования и науки Республики Казахстан Национальная академия образования им. И. Алтынсарина ОКАЗАНИЕ МЕТОДИЧЕСКОЙ ПОМОЩИ ПРИ ПРОВЕДЕНИИ АТТЕСТАЦИИ ПЕДАГОГИЧЕСКИХ КАДРОВ Методическое пособие Астана Рекомендовано к изданию Ученым советом Национальной академии образования им. И. Алтынсарина (протокол № 6 от 20 июля 2015 года) Проведение аттестации педагогических кадров в условиях обновления…»

«Приложение 2 к письму министерства образования и науки Краснодарского края от 03.03.2015г. № 47-2556/15-14 Методические рекомендации по написанию работ на Всероссийский конкурс в области педагогики, работы с детьми и молодежью до 20 лет «За нравственный подвиг учителя» Москва 2015 г. Аннотация Данные методические рекомендации представляют собой специально структурированную информацию, определенный порядок и логику подготовки материала для участия во Всероссийском конкурсе в области педагогики,…»

«Государственное бюджетное образовательное учреждение высшего профессионального образования «Волгоградский государственный медицинский университет» Министерства здравоохранения Российской Федерации Кафедра социальной работы с курсом педагогики и образовательных технологий Социология учебно-методическое пособие для студентов, обучающихся по направлению подготовки 080200 «Менеджмент» Волгоград 2014 Составители: заведующий кафедрой социальной работы с курсом педагогики и образовательных технологий,. ..»

2016 www.сайт — «Бесплатная электронная библиотека — Методички, методические указания, пособия»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам , мы в течении 1-2 рабочих дней удалим его.

Белошистая А.В. Методика обучения математике в начальной школе

М.: Владос, 2007. — 456 с. — (Вузовское образование).

Общие вопросы методики преподавания математики.
Изучение чисел в начальной школе.
Изучение арифметических действий в начальной школе.
Изучение величин в начальной школе.
Геометрический материал в программе начальных классов.
Алгебраический материал в программе начальных классов.
Доли и дроби в курсе математики начальных классов.
Решение задач в начальной школе.
Методическая подготовка учителя к обучению математике в начальной школе.
Личностно-ориентированное обучение на уроках математики в начальной школе.

Истомина Н.Б. Методика обучения математике в начальных классах

Учебное пособие для студентов средних и высших педагогических учебных заведений. — М.: Академия, 2001. — 288 с. — (Педагогическое образование).

Б айрамукова П.У., Уртенова А.У. Методика обучения математике в начальных классах: курс лекций

Ростов-на-Дону: Феникс, 2009. — 299 с. — (Библиотека учителя).

Методика преподавания математики как учебный предмет.
Построение начального курса математики.
Характеристика основных понятий начального курса математики и последовательность его изучения.
Развитие младших школьников в процессе обучения математике.
Методика изучения нумерации целых неотрицательных чисел.
Методика изучения арифметических действий в концентре «десяток».
Методика изучения арифметических действий в концентре «сотня».
Методика изучения арифметических действий в концентре «тысяча».
Методика изучения арифметических действий в концентре «многозначные числа».
Текстовая задача и процесс ее решения.
Методика обучения решению составных задач.

Буквенная символика, равенства, неравенства, уравнения.

Методика изучения важнейших величин.
Методика изучения дробей.
Анализ альтернативных программ и учебников по математике для начальной школы. Различные концепции построения начального курса математики.

Виленкин Н.Я., Пышкало А.М. и др. Математика

Виленкин Н.Я., Пышкало А.М., Рождественская В.В., Стойлова Л.П.
Учебное пособие для студентов пед. институтов. — М.: Просвещение, 1977. — 352 с.

Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах

Учебное пособие для учащихся школьных отделений пед. училищ. (спец. № 2001)/Под ред. М.А. Бантовой. -3-е изд., испр. — М.: Просвещение, 1984. — 335 с.: ил.

Общие вопросы методики начального обучения математике.
Методика изучения нумерации целых неотрицательных чисел и арифметических действий над ними.
Обучение решению арифметических задач.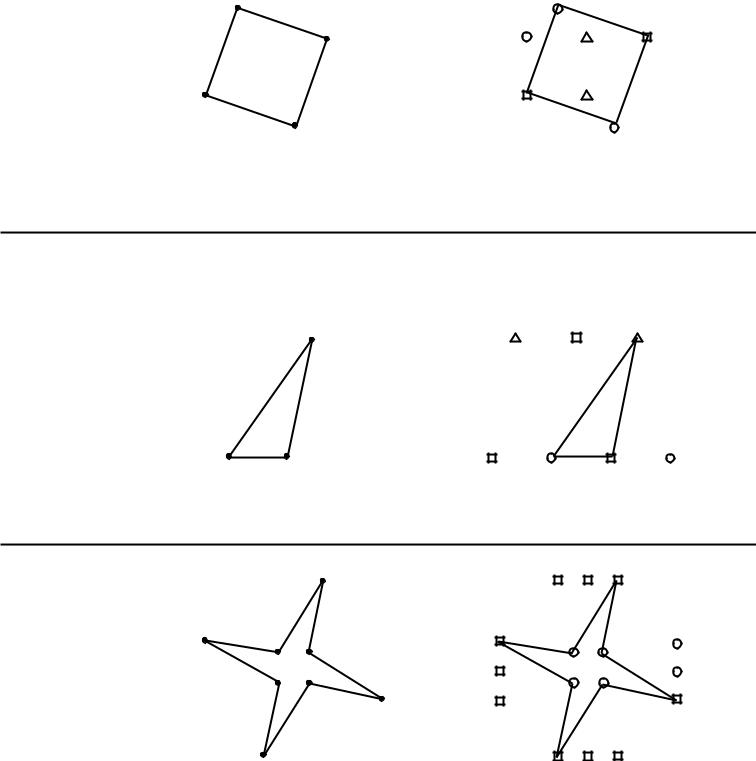
Методика изучения алгебраического материала.
Методика изучения геометрического материала.
Обучение измерению величин.
Методика изучения дробей.
Внеклассная работа по математике и методика ее проведении.

Цель учебного пособия — формирование у будущего учителя методических знаний, умений и опыта творческой деятельности для реализации НА практике идей развивающего обучения младших школьников математике. Пособие будет полезно также учителям, работающим в начальных классах.

Смысл действий сложения и вычитания.
В курсе математики начальных классов находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел (натуральных и нуля), в соответствии с которым сложение целых неотрицательных чисел связано с операцией объединения попарно непересекающихся конечных множеств, вычитание — с операцией дополнения выделенного подмножества. Этот подход легко интерпретируется на уровне предметных действий, позволяя тем самым учитывать психологические особенности младших школьников.

Однако методическая интерпретация данного подхода может быть различной. Например, в учебнике М1М в качестве основного средства формирования у детей представлений о смысле действий сложения и вычитания выступают простые текстовые задачи.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Методика обучения математике в начальных классах, Истомина Н.Б., 2001 — fileskachat.com, быстрое и бесплатное скачивание.

• Математика, 1 класс, Мои учебные достижения, Истомина Н.Б., Шмырёва Г.Г.

Следующие учебники и книги:

• Обучение в 4-м классе по учебнику «Математика», программа, методические рекомендации, тематическое планирование, контрольные работы, Башмаков М.И., Нефёдова М.Г., 2012
• Обучение в 1-м классе по учебнику «Математика» Башмакова М.И., Нефёдовой М.Г., программа, тематическое планирование, методические рекомендации, Башмаков М.И., Нефёдова М.Г., 2013

открытых учебников | Сиявула

Математика

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • класс 7А

      • Марка 7Б

      • Класс 7 (вместе A и B)

    • Африкаанс

      • Граад 7А

      • Граад 7Б

      • Граад 7 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • класс 8А

      • Марка 8Б

      • Оценка 8 (вместе A и B)

    • Африкаанс

      • Граад 8А

      • Граад 8Б

      • Граад 8 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 9А

      • Марка 9Б

      • Оценка 9 (комбинированные A и B)

    • Африкаанс

      • Граад 9А

      • Граад 9Б

      • Граад 9 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • класс 4A

      • класс 4Б

      • Класс 4 (вместе A и B)

    • Африкаанс

      • Граад 4А

      • Граад 4Б

      • Граад 4 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 5А

      • Марка 5Б

      • Оценка 5 (комбинированные A и B)

    • Африкаанс

      • Граад 5А

      • Граад 5Б

      • Граад 5 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • класс 6А

      • Марка 6Б

      • Класс 6 (вместе A и B)

    • Африкаанс

      • Граад 6А

      • Граад 6Б

      • Граад 6 (A en B saam)

  • Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими организациями, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без марочного знака)

Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — указать Сиявула надлежащим образом. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Введение в геометрию | SkillsYouNeed

Когда вы начинаете изучать геометрию, важно знать и понимать некоторые основные концепции.

Эта страница поможет вам понять концепцию размеров в геометрии и решить, работаете ли вы в одном, двух или трех измерениях.

Здесь также объясняется основная терминология и указывается на другие страницы для получения дополнительной информации.

На этой странице представлены точки, линии и плоскости.

На других страницах этой серии рассказывается об углах и формах, включая многоугольники, круги и другие изогнутые формы, а также трехмерные формы.

Что такое геометрия?

---

Геометрия , н.та часть математики, которая рассматривает свойства точек, линий, поверхностей и твердых тел…

---

Словарь английского языка Чемберса, издание 1989 года

Геометрия происходит от греческого слова «измерение земли» и представляет собой визуальное изучение форм, размеров и узоров, а также того, как они сочетаются друг с другом в пространстве. Вы обнаружите, что наши страницы геометрии содержат множество диаграмм, которые помогут вам понять предмет.

Когда вы столкнулись с проблемой, связанной с геометрией, может быть очень полезно нарисовать диаграмму самостоятельно.

---

Работа в разных размерах

Нет, не континуум пространства-времени! Мы говорим о формах в одном, двух и трех измерениях.

То есть объекты, которые имеют длину (одно измерение), длину и ширину (два измерения) и длину, ширину и глубину или высоту (три измерения).

Очки: особый случай: без размеров

A точка — это отдельная точка в пространстве. Он часто представлен точкой на странице, но на самом деле не имеет реального размера или формы.

Вы не можете описать точку с точки зрения длины, ширины или высоты, поэтому она является безразмерной . Однако точку можно описать координатами. Координаты ничего не определяют о точке, кроме ее положения в пространстве по отношению к контрольной точке с известными координатами. Вы встретите координаты точек во многих приложениях, например, когда вы будете рисовать графики или читать карты.

Практически все в геометрии начинается с точки, будь то линия или сложная трехмерная форма.

Линии: Одно измерение

Линия — кратчайшее расстояние между двумя точками. Он имеет длину, но не ширину, что делает его одномерным.

Везде, где встречаются или пересекаются две или более прямых, есть точка, и говорят, что эти две линии имеют общую точку:

---

Отрезки и лучи

Есть два типа линий: те, у которых есть определенная начальная и конечная точки, и те, которые продолжаются вечно.

Линии, которые перемещаются между двумя точками, называются отрезками .Они начинаются с определенной точки и переходят к другой, конечной точке. Как и следовало ожидать, они нарисованы как линия между двумя точками.

Второй тип линии называется луч , и они продолжаются вечно. Их часто проводят в виде линии, начинающейся от точки со стрелкой на другом конце:

---

Параллельные и перпендикулярные линии

Есть два типа линий, которые особенно интересны и / или полезны в математике. Параллельные линии никогда не пересекаются и не пересекаются.Они просто идут вечно бок о бок, как железнодорожные пути. Условием показа параллельности линий на диаграмме является добавление «перьев», которые выглядят как наконечники стрелок.

Перпендикулярные линии пересекаются под прямым углом, 90 °:

---

Плоскости и двумерные формы

Теперь, когда мы рассмотрели одно измерение, пора перейти к двум.

Плоскость — это плоская поверхность, также известная как двумерная. Технически он неограничен, что означает, что он продолжается вечно в любом заданном направлении, и поэтому его невозможно нарисовать на странице.

Один из ключевых элементов геометрии — это количество измерений, с которыми вы работаете в любой момент времени. Если вы работаете в одной плоскости, то это либо одна (длина), либо две (длина и ширина). При наличии более чем одной плоскости он должен быть трехмерным, потому что высота / глубина также учитываются.

Двумерные фигуры включают многоугольники, такие как квадраты, прямоугольники и треугольники, у которых есть прямые линии и точки в каждом углу.

Больше о полигонах можно узнать на нашей странице Полигоны .Другие двумерные формы включают круги и любую другую форму, которая включает кривую. Вы можете узнать больше об этом на нашей странице Curved Shapes .

Три измерения: многогранники и изогнутые формы

Наконец, есть еще трехмерных фигур , таких как кубы, сферы, пирамиды и цилиндры.

Чтобы узнать больше об этом, посетите нашу страницу Трехмерные формы .

---

Знаки, символы и терминология

Показанная здесь форма представляет собой неправильный пятиугольник, пятиугольный многоугольник с разными внутренними углами и длинами линий (подробнее об этих формах см. Нашу страницу о Многоугольники ).

Градусы ° — это мера поворота, определяющая размер угла между двумя сторонами.

Углы обычно обозначаются в геометрии с использованием сегмента окружности (дуги), если только они не являются прямым углом, когда они «возведены в квадрат». В данном примере угловые метки обозначены зеленым цветом. См. Нашу страницу на Уголки для получения дополнительной информации.

Отметки (показаны оранжевым цветом) обозначают стороны фигуры одинаковой длины (стороны фигуры совпадают с или совпадают).Одиночные линии показывают, что две вертикальные линии имеют одинаковую длину, а двойные линии показывают, что две диагональные линии имеют одинаковую длину. Нижняя горизонтальная линия в этом примере отличается по длине от остальных 4 линий и поэтому не отмечена. Отметки также могут называться « штриховок ».

Вершина — это точка пересечения линий (линии также называются лучами или ребрами). Множественное число вершин — это вершины. В этом примере пять вершин помечены как A, B, C, D и E.Называть вершины буквами — обычное дело в геометрии.

В замкнутой форме, такой как в нашем примере, математическое соглашение гласит, что буквы всегда должны располагаться в порядке по часовой стрелке или против часовой стрелки. Нашу форму можно описать как «ABCDE», но было бы неправильно обозначать вершины так, чтобы форма была, например, «ADBEC». Это может показаться несущественным, но в некоторых сложных ситуациях очень важно избежать путаницы.

Символ угла ‘’ используется как сокращенный символ в геометрии при описании угла.Выражение ∠ABC является сокращением для описания угла между точками A и C в точке B. Средняя буква в таких выражениях всегда является вершиной угла, который вы описываете — порядок сторон не важен. ABC совпадает с ∠CBA, , и оба описывают вершину B в этом примере.

Если вы хотите записать измеренный угол в точке B в сокращенном виде, вы должны использовать:

m∠ABC = 128 ° (m просто означает «мера»)

или

м∠CBA = 128 °

В нашем примере мы также можем сказать:

м∠EAB = 90 °

м∠BCD = 104 °

---

Почему эти концепции имеют значение?

Точки, линии и плоскости лежат в основе почти всех остальных геометрических концепций.Углы образуются между двумя линиями, начинающимися от общей точки. Фигуры, двухмерные или трехмерные, состоят из линий, соединяющих точки. Плоскости важны, потому что двумерные формы имеют только одну плоскость; трехмерные их два и более.

Другими словами, вам действительно нужно понять идеи на этой странице, прежде чем вы сможете перейти к любой другой области геометрии.

---

Дополнительные материалы по навыкам, которые вам нужны

---

Руководство по навыкам, которые вам нужны

Это руководство из четырех частей познакомит вас с основами математики, от арифметики до алгебры, с остановками между дробями, десятичными знаками, геометрией и статистикой.

Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.

---

9 самых распространенных форм и способы их определения

Вы, наверное, много узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.

В этой статье мы рассмотрим, что такое фигура, а также множество общих фигур, как они выглядят и основные формулы, связанные с ними.

Что такое форма?

Если вас спросят, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но «форма» тоже имеет особое значение — это не просто названия кругов, квадратов и треугольников.

Форма — это форма объекта, а не то, сколько места он занимает или где находится физически, а реальную форму, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.

Форма может иметь любой размер и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Трудно осознать это, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например подставку для книг в форме пирамиды, цилиндрическую банку с овсянкой или он может быть двухмерным и не занимать физического пространства , такого как треугольник, нарисованный на листе бумаги.

Тот факт, что он имеет форму, отличает форму от точки или линии.

Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни вообще никаких размеров.

Линия же одномерная. Он бесконечно тянется в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.

Хотя мы можем представлять точки или линии как фигуры, потому что нам действительно нужно их видеть, на самом деле они не имеют никакой формы. Вот что отличает форму от других геометрических фигур — она ​​двух- или трехмерная, потому что имеет форму.

Кубики, подобные тем, что здесь изображены, представляют собой трехмерные квадраты — обе формы!

Шесть основных типов двумерных геометрических форм

Трудно изобразить форму только на основе определения — что значит иметь форму , но не занимать место? Давайте взглянем на несколько различных форм, чтобы лучше понять, что именно значит быть формой!

Мы часто классифицируем формы по количеству сторон. «Сторона» — это линейный сегмент (часть линии), составляющий часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.

Тип 1: эллипсы

Эллипсы — это круглые, овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.

овал

Овал немного похож на размятый круг — он не совсем круглый, а в некотором роде вытянутый. Однако классификация неточная. Существует много-много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая имеет удлиненную форму, а не идеально круглую, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.

Поскольку овал не является идеально круглым, формулы, которые мы используем для его понимания, должны быть скорректированы.

Также важно отметить, что вычислить окружность овала довольно сложно , поэтому ниже нет уравнения окружности.Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией окружности, потому что даже лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.

Определения

• Большой радиус : расстояние от начала овала до самого дальнего края
• Малый радиус : расстояние от начала овала до ближайшего края

Формулы

• Площадь = $ \ Major \ Radius * \ Minor \ Radius * π $

Круг

Сколько сторон у круга? Хороший вопрос! К сожалению, нет хорошего ответа, потому что «сторон» больше связаны с многоугольниками — двумерной формой как минимум с тремя прямыми сторонами и обычно как минимум с пятью углами. Наиболее знакомые формы — это многоугольники, но у кругов нет прямых сторон и определенно нет пяти углов, поэтому они не являются многоугольниками.

Итак, сколько сторон у круга? Нуль? Один? На самом деле это неактуально — вопрос просто не относится к кругам.

Круг — это не многоугольник, но что это такое? Круг — это двумерная форма (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одинаковом расстоянии от точки в центре. У овала два фокуса в разных положениях, тогда как у круга фокусы всегда находятся в одном и том же положении.

Определения

• Начало: центр окружности
• Радиус: расстояние от начала координат до любой точки на окружности
• Окружность: расстояние по окружности
• Диаметр: длина от одного края круга до другого
• $ \ bo {π} $: (произносится как пирог) 3. 2 $

Тип 2: Треугольники

Треугольники — самые простые многоугольники. У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.

Поскольку существует много видов треугольников, есть лота важных формул треугольника , многие из которых более сложные, чем другие.Основы включены ниже, но даже основы полагаются на знание длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете рассчитать его различные аспекты, используя углы или только некоторые из сторон.

Определения

• Вершина : точка пересечения двух сторон треугольника
• Основание : любая из сторон треугольника, обычно та, что нарисована внизу.
• Высота : расстояние по вертикали от основания до вершины, с которой не связано

Формулы

• Площадь = $ {\ base * \ height} / 2 $
• Периметр = $ \ side a + \ side b + \ side c $

Тип 3: параллелограммы

Параллелограмм — это форма с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами равной длины. Вы могли заметить, что это определение применяется к квадратам и прямоугольникам — это потому, что квадратов и прямоугольников также являются параллелограммами ! Если вы можете рассчитать площадь квадрата, вы можете сделать это с любым параллелограммом.

Определения

• Длина : размер нижней или верхней стороны параллелограмма
• Ширина : размер левой или правой стороны параллелограмма

Формулы

• Площадь : $ \ длина * \ высота $
• Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 $
• Альтернативно, Периметр : $ \ Side * 4 $

Прямоугольник

Прямоугольник — это форма с параллельными противоположными сторонами в сочетании со всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны. В прямоугольнике один набор параллельных сторон длиннее другого, что делает его похожим на вытянутый квадрат.

Поскольку прямоугольник является параллелограммом, вы можете использовать те же формулы для вычисления их площади и периметров.

Квадрат

Квадрат во многом похож на прямоугольник, за одним заметным исключением: все его стороны равны по длине. Как и прямоугольники, квадратов имеют углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является разновидностью прямоугольника, который является разновидностью параллелограмма!

По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, как и для любого другого параллелограмма.

Ромб

Ромб — как вы догадались — разновидность параллелограмма. Разница между ромбом и прямоугольником или квадратом состоит в том, что его внутренние углы на равны только , как и их диагональные противоположности.

Из-за этого, ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр рассчитывается таким же образом, это влияет на способ вычисления площади, поскольку высота уже не такая, как в квадрате или прямоугольнике.

Определение

• Диагональ : расстояние между двумя противоположными вершинами

Формулы

• Площадь = $ {\ Диагональ 1 * \ Диагональ 2} / 2 $

Тип 4: трапеции

Трапеции — это четырехгранные фигуры с двумя противоположными параллельными сторонами.В отличие от параллелограмма трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.

Определения

• Основание : любая из параллельных сторон трапеции
• Ножки : одна из непараллельных сторон трапеции
• Высота : расстояние от одной базы до другой

Формулы

• Площадь : $ ({\ Base_1 \ length + \ Base_2 \ length} / 2) \ altitude $
• Периметр : $ \ Base + \ Base + \ Leg + \ Leg $

Тип 5: Пентагоны

Пятиугольник — это пятиугольник. Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленным внутрь, или вогнутым — с внутренним углом больше 180 градусов.

Поскольку форма более сложная, ее необходимо разделить на более мелкие формы, чтобы вычислить ее площадь.

Определения

• Апофема : линия, проведенная от центра пятиугольника к одной из сторон, ударяющая в сторону под прямым углом.

Формулы

• Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 $
• Площадь : $ {\ Perimeter * \ Apothem} / 2 $

Тип 6: шестиугольники

Шестиугольник — это шестигранная форма, очень похожая на пятиугольник. Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.

Также, как и пятиугольники, формула площади шестиугольника значительно сложнее, чем формула параллелограмма.

Формулы

• Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 + \ Сторона 6 $
• Площадь : $ {3√3 * \ Side * 2} / 2 $
• Альтернативно, Площадь : $ {\ Perimeter * \ Apothem} / 2 $

А как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, например сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение — объем занимаемого пространства, а не только форма, — которое необходимо учитывать при вычислении площади и периметра.

Математика

, включающая двумерные формы, такие как приведенные выше, называется плоской геометрией , потому что она имеет дело конкретно с плоскостями или плоскими формами . Математика, включающая трехмерные формы, такие как сферы и кубы, называется твердотельной геометрией , потому что она имеет дело с твердыми телами, другим словом для трехмерных фигур .

2D-формы составляют те 3D-фигуры, которые мы видим каждый день!

3 основных совета по работе с фигурами

Существует так много типов фигур, что бывает сложно вспомнить, что есть что и как рассчитать их площади и периметры. Вот несколько советов и приемов, которые помогут вам их запомнить!

# 1: Определить многоугольники

Некоторые формы являются многоугольниками, а некоторые нет. Один из самых простых способов сузить кругозор какой-либо формы — это выяснить, является ли это многоугольником.

Многоугольник состоит из прямых, не пересекающихся. Какие фигуры ниже являются многоугольниками, а какие нет?

Круг и овал не являются многоугольниками, поэтому их площадь и периметр рассчитываются по-разному. Узнайте больше о том, как вычислить их, используя $ π $ выше!

# 2: Проверить параллельность сторон

Если фигура, на которую вы смотрите, представляет собой параллелограмм, обычно легче вычислить ее площадь и периметр, чем если бы это не параллелограмм. Но как определить параллелограмм?

Это прямо в названии — параллель. Параллелограмм — это четырехсторонний многоугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы — это параллелограммы.

Квадраты и прямоугольники используют одни и те же основные формулы для вычисления площади длины, умноженной на высоту. Их также очень легко найти по периметру, поскольку вы просто складываете все стороны вместе.

С ромбами все усложняется, потому что вы умножаете диагонали и делите их на два.

Чтобы определить, на какой параллелограмм вы смотрите, спросите себя, все ли у него углы 90 градусов.

Если да, то это квадрат или прямоугольник . Прямоугольник имеет две стороны, которые немного длиннее других, тогда как у квадрата все стороны равны. В любом случае, вы вычисляете площадь, умножая длину на высоту и периметр, складывая все четыре стороны вместе.

Если нет, вероятно, это ромб, который выглядит так, как если бы вы взяли квадрат или прямоугольник и наклонили его в любом направлении. В этом случае вы найдете площадь, умножив две диагонали вместе и разделив на два. Периметр определяется так же, как периметр квадрата или прямоугольника.

# 3: Подсчитайте количество сторон

Формулы для фигур, у которых нет четырех сторон, могут быть довольно сложными, поэтому лучше всего их запомнить. Если у вас возникают проблемы с их правильностью, попробуйте запомнить греческие слова для чисел, , например:

Tri : три, как в triple, что означает три чего-то

Tetra : четыре, как количество квадратов в блоке Tetris

Penta : пять, как в Пентагоне в Вашингтоне Д.C., представляющий собой большое здание в форме Пентагона

Hexa : шесть, как в шестнадцатеричном формате, шестизначные коды, часто используемые для цвета в веб-дизайне и графическом дизайне

Септа : семь, как в Септе, женском духовенстве религии Игры престолов, имеющей семь богов

Octo : восемь, как в восьми лапах осьминога

Эннеа : девять, как в эннеаграмме, общая модель человеческих личностей

Дека : десять, как в десятиборье, в котором спортсмены завершают десять видов

Что дальше?

Если вы готовитесь к ACT и вам нужна дополнительная помощь по вашей геометрии, ознакомьтесь с этим руководством по координатной геометрии!

Если вы больше относитесь к типу SAT, это руководство по треугольникам в разделе геометрии SAT поможет вам подготовиться к тесту !

Не можете насытиться математикой ACT? Это руководство по полигонам на ACT поможет вам подготовиться с помощью полезных стратегий и практических задач!

Параллельные стороны: определение и концепция — видео и стенограмма урока

Свойства параллельных сторон

Когда фигура имеет пару параллельных сторон, это придает форме определенные уникальные свойства.

Трапеция с одной парой параллельных сторон.

Посмотрите на эту трапецию. Обычно, когда у фигуры есть пара параллельных сторон, они составляют основу фигуры. Эта трапеция имеет два основания, каждое из которых является одной из двух параллельных сторон.

Кроме того, когда у фигуры есть пара параллельных сторон, высота фигуры будет одинаковой независимо от того, на сколько вы ее растянете. Возьмем, к примеру, эту трапецию.Если бы я растянул фигуру, она все равно имела бы ту же высоту.

Трапеция имеет одинаковую высоту даже в растянутом состоянии из-за параллельности сторон.

Символ параллельности

Есть два способа математически обозначить, что две стороны параллельны друг другу. Один из способов — написать это математическим символом. Другой способ — отметить это прямо на фигуре, используя совпадающие стрелки на параллельных сторонах.

Параллельный символ.

Если бы у фигуры было более одной пары параллельных сторон, вы бы отметили разницу, добавив еще одну стрелку ко второй паре параллельных сторон.

Разметка двух пар параллельных сторон.

Обратите внимание, как у этого прямоугольника две пары параллельных сторон, и как я пометил каждую пару по-разному.У второй пары есть две совпадающие стрелки вместо одной. Это позволяет мне знать, что, хотя каждая пара параллельна, две пары не параллельны друг другу.

Фигуры с параллельными сторонами

Есть несколько форм, у которых параллельные стороны являются отличительной особенностью. Наиболее распространены параллелограмм, прямоугольник, квадрат и трапеция. Это те, о которых вы чаще всего слышите, как о параллельных сторонах.

Обычные формы с параллельными сторонами.

Трапеция имеет одну пару параллельных сторон. Параллелограмм, прямоугольник и квадрат имеют две пары параллельных сторон.

Другие менее распространенные формы с параллельными сторонами включают любые «-угольники» с четным числом сторон, например шестиугольник, восьмиугольник, десятиугольник и т. Д.

Шестиугольник и восьмиугольник с параллельными сторонами.

Пока эти «-угольники» имеют стороны одинаковой длины, у них будет по крайней мере одна пара параллельных сторон.Глядя на показанные здесь шестиугольник и восьмиугольник, вы видите, что у них есть несколько пар параллельных сторон?

Резюме урока

Параллельные стороны — уникальное свойство определенных форм. Это стороны, которые никогда не встретятся и всегда находятся на одинаковом расстоянии друг от друга. Некоторые формы с параллельными сторонами включают параллелограмм, прямоугольник, квадрат, трапецию, шестиугольник и восьмиугольник.

Краткий обзор урока

Фигуры параллельны, если у них есть линии, которые всегда находятся на одинаковом расстоянии друг от друга и никогда не будут пересекаться или касаться друг друга.Некоторые формы с параллельными сторонами включают параллелограмм, прямоугольник, квадрат, трапецию, шестиугольник и восьмиугольник.

У трапеции одна пара параллельных сторон.

Результаты обучения

После того, как вы усвоили урок, вы можете с уверенностью приступить к следующему:

• Иллюстрировать параллельные линии
• Распознавать свойства параллельных сторон
• Обозначьте фигуры с параллельными сторонами математическим символом
• Нарисуйте фигуры с параллельными сторонами

Видео: групповые фигуры или изображения

Группировка фигур позволяет вращать, переворачивать, изменять размер или располагать их вместе, как если бы они были одной фигурой или объектом.

Группирование фигур, изображений и других объектов

1. Нажмите и удерживайте Ctrl, щелкая фигуры, изображения или другие объекты для группировки.

2. Выполните одно из следующих действий:

   • Чтобы сгруппировать формы и другие объекты, на вкладке ИНСТРУМЕНТЫ ЧЕРТЕЖА ФОРМАТ щелкните Группа > Группа .

   • Чтобы сгруппировать изображения, на вкладке ИНСТРУМЕНТЫ ИЗОБРАЖЕНИЙ ФОРМАТ щелкните Группа > Группа .

     Примечания:

     • Вы можете вносить изменения во всю группу, например добавлять заливку формы или эффект, или эффект к изображению.

     • После создания группы вы все еще можете работать с отдельным элементом в группе. Выберите группу, а затем щелкните элемент, чтобы выбрать его.

     • Вы можете создавать группы внутри групп. Например, добавьте еще один элемент поверх существующего для создания сложных чертежей.

Сгруппируйте фигуры, если у вас есть несколько фигур, которые вы хотите рассматривать как единое целое.

Например, этот прямоугольник с текстом внутри выглядит как одно целое, но на самом деле это две формы.

Прямоугольник представляет собой одну фигуру — когда я щелкаю по ней, мы видим, что она выделена, а текст содержится во второй фигуре, текстовом поле.

Итак, если я перемещаю прямоугольник — я наведу и перетащу четырехконечный курсор, чтобы сделать это — текст в его текстовом поле останется позади.

Чтобы переместить две фигуры вместе, мне нужно сначала выделить их обе.

Нажмите, чтобы выбрать прямоугольник, затем нажмите и удерживайте Ctrl, пока я нажимаю, чтобы выделить текстовое поле.

Выбрав обе формы, я могу перемещать их как единое целое.

Но для этого мне всегда придется выбирать обе формы.

Чтобы этого избежать, я сгруппирую фигуры.

Выделив фигуры, я наведу на них указатель, щелкните правой кнопкой мыши четырехконечный курсор, наведите указатель на Group и щелкните Group . Это группирует их в единое целое.

Теперь у них есть только одно поле выбора, и они перемещаются вместе.

Я добавил еще два прямоугольника с текстом и сгруппировал каждый прямоугольник с его текстовым полем.

Итак, каждая фигура и ее текст перемещаются как единое целое.

Затем я хочу работать со всеми формами как единым целым.

Сначала я выберу их — на этот раз, чтобы выделить, я собираюсь обвести большую рамку вокруг фигур.

Затем я щелкну правой кнопкой мыши по одной из выбранных фигур, наведу указатель на Group и щелкните Group .

Фигуры сгруппированы. Поле выбора теперь охватывает их всех, и они движутся как одно целое.

Хорошим преимуществом группировки фигур является то, что я могу изменять их как единое целое.

Например, чтобы увеличить их, я указываю на угол и перетаскиваю двухконечный курсор вниз по диагонали.

Я тоже могу форматировать все фигуры сразу.

Выбрав группу, я нажимаю на вкладку ИНСТРУМЕНТЫ ДЛЯ ЧЕРТЕЖИ ФОРМАТ и нажимаю Эффекты формы .

Затем я укажу на Shadow и выберу эффект тени.

Относится к группе.

Grouping также позволяет мне размещать фигуры как единое целое.

Не снимая выделения с группы, нажимаю Align Objects на вкладке FORMAT .

Затем я нажимаю Align Center , чтобы центрировать группу по горизонтали на слайде.

Затем я снова нажимаю Align Objects и нажимаю Align Middle , чтобы центрировать группу по вертикали.

Наверх далее: Группирование и форматирование изображений .

Рисование основных фигур | Справка SketchUp

Многие модели начинаются с основных форм. В SketchUp инструменты фигур помогают рисовать прямоугольники, круги и многоугольники. Вы найдете эти инструменты на панели инструментов «Приступая к работе», на панели инструментов «Рисование» и на панели инструментов «Большой набор инструментов».

Рисование прямоугольника или квадрата

В SketchUp прямоугольники можно рисовать практически где угодно:

• На плоскости
• На вертикальной плоскости
• На существующих забоях
• Отдельно от существующей геометрии (выровнено по плоскости осей)
• На основе существующей геометрии

Чтобы нарисовать прямоугольник с помощью инструмента «Прямоугольник», выполните следующие действия:

1. Выберите инструмент Прямоугольник () на панели инструментов или нажмите клавишу R .Курсор изменится на карандаш с прямоугольником.

   Совет: Чтобы начать сначала в любой момент во время этих шагов, нажмите Esc .

2. Щелкните, чтобы установить первую угловую точку прямоугольника. .
3. Щелкните, чтобы установить первую угловую точку прямоугольника. Чтобы выровнять плоскость вашего прямоугольника с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию, как описано далее в этом разделе.
4. Щелкните, чтобы установить первую угловую точку прямоугольника.Чтобы выровнять плоскость вашего прямоугольника с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию, как описано далее в этом разделе. Если вы предпочитаете рисовать прямоугольник из центра, нажмите клавишу Ctrl (Windows) или клавишу Option (macOS).
5. Переместите курсор по диагонали, чтобы найти требуемый размер и форму прямоугольника. Чтобы нарисовать прямоугольник с точными размерами, используйте поле «Измерения», в котором при перемещении курсора отображаются размеры вашего прямоугольника.Чтобы помочь вам разместить прямоугольник относительно осей рисования или другой геометрии, механизм вывода SketchUp отображает на экране подсказки. Когда появится нужный вывод, переходите к шагу 4. Выводы в поле «Измерения» и в инструменте «Прямоугольник» объясняются немного позже в этом разделе.
6. Щелкните еще раз, чтобы задать вторую угловую точку прямоугольника. Ваша фигура отображается с лицом, как показано на следующем рисунке.
7. Щелкните еще раз, чтобы задать вторую угловую точку прямоугольника.Или, если вы рисуете прямоугольник из центра, щелкните еще раз, чтобы установить любую угловую точку. Ваша фигура отображается с лицом, как показано на следующем рисунке.

Когда вы рисуете прямоугольник, поле «Измерения» помогает вам моделировать точно следующим образом:

• Установите длину и ширину. Введите значение длины, запятую, значение ширины и нажмите Введите . Например, введите 8 ‘, 20’ и нажмите . Введите . Если вы вводите только число или числа, SketchUp использует текущую настройку единиц измерения документа.Вы также можете переопределить настройку единиц измерения документа, указав британские (например, 1’6 «) или метрические (например, 3,652 м ) единицы.
• Укажите только длину или ширину. Если ввести значение и запятую ( 3 ‘, ), новое значение будет применено к первому измерению, а второе измерение не изменится. Точно так же, если вы введете запятую, а затем значение (, 3 ’), изменится только второе измерение.
• Измените положение прямоугольника отрицательными числами. Если вы вводите отрицательное значение ( –24, –24 ), SketchUp применяет это значение в направлении, противоположном тому, которое вы указали при рисовании.

Совет: Нет необходимости щелкать поле «Измерения» перед вводом значения. Во время рисования поле «Измерения» ждет, когда вы введете точные измерения, если вы захотите это сделать. Кроме того, пока вы не выберете другой инструмент или не нарисуете другой прямоугольник, вы можете использовать поле «Измерения», чтобы изменять размеры прямоугольника сколько угодно раз.

Примечание: Если вы используете неанглийскую клавиатуру, используйте запятую для обозначения десятичного разряда и точку с запятой для разделения размеров. Например, вы можете ввести две стороны прямоугольника как: 7,6 м; 4,3 м

Когда вы перемещаете курсор с выбранным инструментом «Прямоугольник», механизм вывода SketchUp отображает следующие подсказки:

Необходимо выровнять плоскость прямоугольника с осью рисования или другой геометрией? Клавиши со стрелками могут помочь, как описано в следующей таблице.

Ключ-модификатор	: плоскость прямоугольника фиксируется так, чтобы она совпадала с…	Как это выглядит на экране
Стрелка влево	Зеленая ось
Стрелка вверх	Синяя ось
Стрелка вправо	Красная ось
Стрелка вниз	Предполагаемая геометрия

На видео вы можете увидеть эти функции инструмента «Прямоугольник» в действии.

Рисование повернутого прямоугольника

Инструмент «Повернутый прямоугольник» может пригодиться, когда вам нужно нарисовать прямоугольник, грань которого расположена под углом к ​​красной, зеленой или синей осям SketchUp по умолчанию или к другой геометрии.

Как и инструмент «Прямоугольник», инструмент «Прямоугольник с поворотом» позволяет создавать точные прямоугольники и квадраты и выводит на экран выводы, которые помогут вам при рисовании. Однако, когда вы создаете прямоугольник с помощью инструмента «Повернутый прямоугольник», вы также располагаете прямоугольник под углом.На следующем рисунке показан пример прямоугольника, созданного с помощью инструмента «Прямоугольник с поворотом».

Чтобы создать повернутый прямоугольник, выполните следующие действия:

1. На панели инструментов в меню «Инструменты для фигур» выберите инструмент «Прямоугольник с поворотом» (). Или выберите Рисование> Фигуры> Повернутый прямоугольник в строке меню.
2. (Необязательно) Нажмите клавишу со стрелкой, чтобы установить плоскость для повернутого прямоугольника в соответствии с таблицей, приведенной ранее в этой статье. Например, нажмите клавишу со стрелкой влево, чтобы ограничить плоскость повернутого прямоугольника зеленой плоскостью.
3. Щелкните один раз, чтобы задать первый угол прямоугольника.
4. Создайте первый край вашего повернутого прямоугольника. Сделать это можно двумя способами:
   • Введите точное измерение и нажмите Введите .
   • Или переместите курсор туда, где вы хотите разместить вторую конечную точку этого ребра, используя механизм вывода SketchUp, чтобы расположить конечную точку относительно осей или другой геометрии, как показано на следующем рисунке, а затем щелкните.

     Совет: По завершении этого шага вы можете использовать несколько клавиш-модификаторов. Удерживайте нажатой клавишу Shift , чтобы ограничить первый край его текущим направлением. Клавиша Alt (Windows) или Command (macOS) блокирует плоскость транспортира. Или клавиши со стрелками снова могут помочь вам выровнять первый край по оси. Просто нажмите кнопку со стрелкой, которая соответствует желаемому выравниванию, как объяснялось ранее в этом разделе. Например, нажмите клавишу со стрелкой вправо, чтобы ограничить первый край так, чтобы он был выровнен по красной оси.

5. На этом этапе вы устанавливаете ширину и угол вашего прямоугольника. Вы можете установить эти значения несколькими способами:
   • Введите угол и ширину в поле «Измерения», следуя подсказке.
   • Введите ширину и угол в поле «Измерения», следуя подсказке.
   • Переместите транспортир, чтобы установить угол, и переместите курсор от центра транспортира, чтобы установить ширину, как показано на следующем рисунке. Чтобы ограничить угол, удерживайте клавишу Shift . Щелкните, чтобы завершить создание повернутого прямоугольника.

Совет: Нажмите клавишу Alt (Windows) или Command (macOS), чтобы установить базовую линию транспортира в текущем положении курсора, а затем переместите курсор, чтобы измерить угол от установленной базовой линии. Этот метод полезен, если вы хотите измерить угол от точки, отличной от базовой линии, установленной на шаге 3. Появится пунктирная линия, чтобы вы могли увидеть новую базовую линию.

Примечание: , если вы используете неанглийскую клавиатуру, вы захотите использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения». Например, вы можете ввести угол и ширину второй кромки как 43,2; 8,2 м , чтобы получить угол 43,2 градуса и длину 8,2 метра.

Примечание: , если вы используете неанглийскую клавиатуру, вы захотите использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения». Например, вы можете ввести ширину и угол второй кромки как 8,2 м; 43,2 , чтобы получить ширину 8,2 метра и угол 43,2 градуса.

Рисование круга или эллипса

Прежде чем рисовать круг, полезно понять, как SketchUp создает объекты круга:

• Круговые объекты имеют радиус и соединяют несколько отрезков линии.
• Эти сегменты действуют как одна линия в том смысле, что они могут определять край грани и разделять грань.Кроме того, при выборе одного сегмента выделяется весь круговой объект.
Механизм вывода
• SketchUp по-прежнему видит сегменты в круге. Итак, если вы наведете указатель мыши на окружность объекта круга, вы увидите выводы конечной и средней точки.

Чтобы нарисовать круг, выполните следующие действия:

1. На панели инструментов выберите инструмент Окружность () в раскрывающемся меню рядом с инструментом Прямоугольник. Или нажмите клавишу C . Курсор изменится на карандаш с кружком, а в поле «Измерения» будет указано количество сторон по умолчанию: 24, как показано на рисунке. Чтобы изменить количество сторон, вы можете ввести значение сейчас или подождать, пока не закончите рисовать круг.
2. Щелкните, чтобы разместить центральную точку круга. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после рисования круга.
3. Щелкните, чтобы разместить центральную точку круга. Чтобы выровнять плоскость вашего круга с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию.Например, стрелка вверх выравнивает плоскость круга по синей оси. Подробную информацию см. В таблице в разделе Рисование прямоугольника или квадрата. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после рисования круга.
4. Переместите курсор из центральной точки, чтобы определить радиус круга. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Нажмите Esc в любой момент, чтобы начать все заново.
5. Щелкните, чтобы закончить круг. SketchUp создает лицо в форме круга, как показано на рисунке.
   
   
6. (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый круг, вы можете использовать поле «Измерения», чтобы изменить радиус круга или количество сторон следующим образом:
   
   • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
   • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . Кроме того, вы можете удерживать клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или —, чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете французско-канадскую клавиатуру, удерживайте клавиши Ctrl (Microsoft Windows) и + / = , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или –, чтобы уменьшить сегменты.
   • Чтобы изменить радиус: Введите число и единицу измерения (при желании), например, 6 дюймов , 8 ’, 34 см или 7 м . Затем нажмите Введите или Верните . Совет: Диалоговое окно Entity Info предлагает удобный способ редактировать значения сторон и радиуса в любое время. Дополнительные сведения см. В разделе «Редактирование фигур» далее в этой статье.

Чтобы нарисовать эллипс или овал, выполните следующие действия:

1. Нарисуйте окружность с помощью инструмента Окружность .
2. Выберите инструмент Масштаб ().
3. Щелкните кружок. Вокруг круга отображается ограничивающая рамка с восемью зелеными ручками.
4. Щелкните одну из средних ручек (не одну из угловых) и переместите мышь, чтобы превратить круг в эллипс, как показано здесь.
5. Нажмите еще раз, когда закончите масштабировать круг.

Рисование многоугольника

Вы можете создавать полигональные объекты с помощью инструмента «Многоугольник». (В этом нет ничего удивительного.) Однако вот несколько фактов, которые вы можете не знать о многоугольниках, но которые полезно знать при их рисовании:

• В SketchUp многоугольник имеет радиус и 3 или более сторон. Таким образом, размер вашего многоугольника измеряется от центральной точки, а количество сторон определяет тип рисованного многоугольника. Пятиугольник в виде 5 сторон; восьмиугольник имеет 8 сторон.
• Многоугольники действуют как одна линия, так как они могут определять край грани, а также разделять грань. При выборе одной стороны многоугольника выделяется весь многоугольник.
• Механизм вывода SketchUp интерпретирует каждую сторону многоугольника как сегмент. Когда вы наводите курсор на многоугольник, вы видите конечную точку, среднюю точку и исходные точки.
• Вы можете рисовать многоугольники на гранях или отдельно от существующей геометрии.

Чтобы нарисовать многоугольник, выполните следующие действия:

1. Выберите инструмент Многоугольник () на панели инструментов.Курсор изменится на карандаш с многоугольником. В поле «Измерения» указано текущее количество сторон. Чтобы изменить количество сторон многоугольника, вы можете ввести числовое значение сейчас или дождаться завершения рисования.
2. Щелкните, чтобы разместить центральную точку многоугольника. В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после рисования многоугольника.
3. Щелкните, чтобы разместить центральную точку многоугольника. Чтобы выровнять плоскость вашего многоугольника с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию.Например, стрелка вверх выровняет плоскость многоугольника по синей оси. Подробнее см. В предыдущей таблице в разделе «Рисование прямоугольника или квадрата». В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после рисования многоугольника.
4. Переместите курсор из центральной точки, чтобы определить радиус многоугольника. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Чтобы указать радиус, введите значение и нажмите Введите .Вы также можете нажать Esc , чтобы начать все заново.
5. Щелкните второй раз, чтобы закончить многоугольник. Здесь вы видите 5-сторонний многоугольник.
   
6. (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый многоугольник, вы можете использовать поле Измерения, чтобы изменить радиус или количество сторон следующим образом:
   • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите .
   • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . Кроме того, вы можете удерживать клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или —, чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете французско-канадскую клавиатуру, удерживайте клавиши Ctrl (Microsoft Windows) и + / = , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или –, чтобы уменьшить сегменты.
   • Чтобы изменить радиус: Введите число и единицу измерения (при желании), например, 6 дюймов , 8 ’, 34 см или 7 м . Затем нажмите Введите или Верните .

   Совет: Хотя инструмент «Многоугольник» работает аналогично инструменту «Круг», разница между инструментами становится очевидной, когда вы нажимаете / вытягиваете круг или многоугольник в трехмерную форму.Края круга выглядят гладкими, но края многоугольника имеют четкие стороны, как показано здесь.

   
   

В этом видеоролике вы можете увидеть, как инструменты «Круг» и «Многоугольник» демонстрируют все свои трюки.

Редактирование форм

Диалоговое окно «Информация об объекте» позволяет изменить радиус или стороны круга или многоугольника в любое время после создания формы. Вот как:

1. Щелкните правой кнопкой мыши край (не грань) круга или многоугольника, который вы хотите отредактировать.
2. Выберите Entity Info из появившегося контекстного меню, как показано здесь.
   
3. На панели «Информация об объекте» щелкните поле Radius или Segments , измените значение и нажмите , введите (Microsoft Windows) или , верните (Mac). После того, как вы нажмете Enter или Return, ваша форма немедленно отобразит ваши изменения.

SketchUp не позволяет изменять ширину или длину прямоугольника в любое время.Если вы уже выбрали другой инструмент или нарисовали дополнительные прямоугольники, вам нужно стереть прямоугольник, который вы хотите изменить, и перерисовать его. Подробнее см. Рисование прямоугольника. Или измените размер прямоугольника с помощью инструмента «Масштаб», если вам не нужно вводить точные размеры.

Конечно, вы можете сделать гораздо больше, чем просто изменить размер фигуры. Вы можете превратить 2D-форму в 3D-форму с помощью инструмента Push / Pull. Вы можете искажать формы с помощью инструмента «Перемещение» или масштабировать всю или часть модели.

форм молекул

В двухатомной молекуле (X ₂ или XY) существует только одна связь, и полярность этой связи определяет полярность молекулы: если связь полярна, молекула полярна, и если связь неполярная, молекула неполярна.

В молекулах с более чем одной связью обе формы и полярность связи определяют, является ли молекула полярной . А молекула должна содержать полярные связи, чтобы молекула была полярной, но если полярные связи выровнены точно напротив друг друга, или если они достаточно симметричны, полярности связей сокращаются, делая молекула неполярная. (Полярность — это векторная величина, поэтому как необходимо учитывать величину и направление .)

Например, рассмотрим точечную структуру Льюиса для углекислый газ. Это линейная молекула, содержащая два полярных углерод-кислородные двойные связи. Однако, поскольку полярные связи указывают ровно на 180 друг от друга, полярности связи сокращаются, и молекула неполярна. (В качестве аналогии вы можете подумать, что это как игра в перетягивание каната между двумя командами, которые тянут за веревку одинаково сложно.)

Молекула воды также содержит полярные связи, но поскольку это изогнутая молекула, связи расположены под углом друг к другу около 105.Они отменяют , а не , потому что не указывают точно по направлению друг к другу, и есть общий диполь, идущий от водородный конец молекулы по направлению к кислородному концу молекулы; вода, следовательно, является полярной молекулой:

Молекулы, в которых все атомы, окружающие центральный атом такие же, как правило, неполярный, если нет неподеленных пар на центральном атоме. Если некоторые из атомов, окружающих центральный атом различны, однако молекула может быть полярной. Например, углерод тетрахлорид, CCl ₄ , неполярный, но хлороформ, CHCl ₃ , и метилхлорид, CH ₃ Cl полярны:

Полярность молекулы сильно влияет на ее физические свойства. Более полярные молекулы имеют более сильную межмолекулярные силы между ними и, как правило, имеют более высокую температуру кипения точки (а также другие различные физические свойства).

В таблице ниже показано, соответствуют ли примеры в предыдущие разделы полярны или неполярны. Для видов, у которых есть общая сумма, вместо этого используется термин начисленная, поскольку термины полярные и неполярные на самом деле не применимы к заряженным видам; заряжен виды, по определению, по существу полярны. Одинокие пары на каком-то внешнем атомы опущены для ясности.

	Формула	Льюис Строение	3D-структура Форма Полярность	Пояснение
1.	CH 4		четырехгранный неполярный	Облигация CH неполярный, так как C и H различаются всего на 0,35 единицы электроотрицательности.
2.	NH 3		тригональная пирамидальный полярный	С этого момента молекула не плоская, связи NH не указывают непосредственно друг на друга, и их полярности не отменяют вне.Кроме того, есть небольшой диполь в направлении одинокой пары.
3.	H 2 O		гнутый полярный	С этого момента молекула изогнута, связи ОН не указывают прямо на друг друга, и их полярности не исключают друг друга.
4.	H 3 O +		тригональная пирамидальный заряжено	С этого момента вид заряжен, термины полярный и неполярный не имеющий отношения.
5.	HCN		линейный полярный	Линейные молекулы обычно неполярны, но в этом случае не все атомы связанные с центральным атомом такие же.Облигация CN полярный, и не компенсируется неполярной связью CH.
6.	CO 2		линейный неполярный	Полярный C = O облигации ориентированы на 180 ° друг от друга. Полярность этих связей аннулируется, делая молекулу неполярной.
7.	CCl 4		четырехгранный неполярный	Полярный CCl облигации ориентированы 109.5 друг от друга. Полярность этих связей аннулируется, делая молекулу неполярной.
8.	COCl 2		тригонально планарная полярный	Тригональный планарный молекулы обычно неполярны, но в этом случае не все атомы, связанные с центральным атомом, такие же.В полярности связи не отменяются полностью, и молекула полярна. (Если бы было три О или три Cl прикрепленный к центральной точке C, он будет неполярным.)
9.	О 3		гнутый полярный	Изогнутые молекулы всегда полярны.Хотя кислородно-кислородные связи неполярный, неподеленная пара на центральном O вносит некоторый полярность к молекуле.
10.	CO 3 2-		тригонально планарная заряжено	С этого момента вид заряжен, термины полярный и неполярный не имеющий отношения.
11.	С 2 В 6		четырехгранный неполярный	Оба атома углерода четырехгранные; так как облигации CH и облигации CC являются неполярная, молекула неполярная.
12.	С 2 В 4		тригонально планарная неполярный	Оба атома углерода тригонально плоские; так как облигации CH и облигации CC неполярны, молекула неполярна.
13.	Канал 3 Канал 2 ОН		C: четырехгранник O: изогнутый полярный	CC и CH связи не влияют на полярность молекулы, но связи CO и OH полярны, так как форма вокруг атом O изогнут, молекула должна быть полярной.
14.	BF 3		тригонально планарная неполярный	С этого момента молекула плоская, все три полярные связи BF находятся в одна и та же плоскость, ориентированная на 120 ° друг от друга, в результате чего молекула неполярная.
15.	НЕТ		линейный полярный	Поскольку есть только одна связь в этой молекуле, и связь полярная, молекула должна быть полярной.
16.	PCl 5		тригональная бипирамидальный неполярный	Связь PCl в экваториальные положения на этой молекуле ориентированы 120 друг от друга, и их полярности связи компенсируются.Связи PCl в осевых положениях отстоят на 180 от друг друга, и их полярности связи также компенсируются.
17.	SF 6		восьмигранный неполярный	Облигации SF в все эти молекулы удалены друг от друга на 90 °, и их полярности облигаций сокращаются.
18.	SF 4		качели полярный	Облигации SF в осевые позиции разнесены на 90, а их полярности связи отменяет.В экваториальных позициях, так как одна позиция поглощается одинокой парой, они не сокращаются, и молекула полярна.
19.	XeF 4		плоский квадрат неполярный	Облигации XeF все ориентированы на 90 градусов друг от друга, и их связь полярности компенсируются.Одинокие пары находятся на расстоянии 180 от друг друга, и их небольшая полярность также уравновешивается.
20.	H 2 SO 4		S: четырехгранный O: изогнутый полярный	Эта молекула полярный из-за изогнутых связей HOS, которые присутствуют в Это. Оставьте комментарий Отменить ответ Комментарий Имя Email Сайт Прокрутка вверх