Как отмерить 30 градусов без транспортира, как построить угол 30?
Ключом к подобным «клетчатым» построениям углов является волшебное число 11. Если по клеткам нарисовать прямоугольный треугольник с одним катетом, равным 11 клеток, то выбор другого катета будет для этого треугольника давать следующие острые углы:
- 1 клетка — 5° и 85°
- 2 клетки — 10° и 80°
- 3 клетки — 15° и 75°
- 4 клетки — 20° и 70°
- 5 клеток — 25° и 65°
Запомнить нетрудно: каждая клетка добавляет по пять градусов, и так до пяти клеток. Погрешность составит около половины градуса для катетов 5 и 11 клеток, в остальных случаях она значительно меньше.
Ещё полезно помнить, что прямоугольный треугольник с катетами 8 и 11 клеток имеет острый угол 36° (с очень хорошей точностью). Это позволяет строить правильные пятиугольники и десятиугольники.
Волшебные свойства числа 11 на этом не заканчиваются. Выпишем последовательно натуральные числа: 3,4,5,6,7,8. Будем выбирать из них «крайние» пары: 3 и 8, 4 и 7, 5 и 6. Как видно, в сумме они все дают опять-таки 11. Если брать эти пары в качестве катетов, то получающиеся прямоугольные треугольники будут иметь следующие углы:
- 3 и 8 клеток — 20° и 70° (менее точно, чем для катетов 4 и 11 клеток)
- 4 и 7 клеток — 30° и 60°
- 5 и 6 — 40° и 50°
Ошибка составит около половины градуса для катетов 3 и 8 клеток, а в двух других случаях будет значительно меньше.
Отсюда следует способ построения по клеткам равностороннего треугольника: если взять горизонтальный или вертикальный отрезок 8 клеток и от его середины отступить в перпендикулярном направлении на 7 клеток, то получившийся равнобедренный треугольник будет практически равносторонним.
отмерить угол без транспортира
Неплохо помнить ещё две пары катетов, дающих следующие острые углы:
- 2 и 9 клеток — 12° и 78°
- 1 и 10 клеток — 6° и 84°
Как видно, в сумме они составляют опять-таки 11. Наибольшая погрешность снова около половины градуса (у пары 2 и 9 клеток).
Эта клетчатая тригонометрия позволяет без проблем строить любые углы с шагом 5° без транспортира при неплохой точности.
Как построить угол в 30 градусов, без транспортира?
6. Как построить углы 30, 60, 90, 120, 150 градусов, циркулем?
Измерения и построение углов при проведении различных работ. Золотой египетский треугольник.
Как сложить бумагу для снежинки из 6 лучей (пошаговая инструкция)
Напротив угла в 30 градусов лежит катет равный половине гипотенузы
? АВС — равнодедренный, следовательно высота треугольника является и медианой и бессектриссой. Бессиктрисса ВД делит отрезок АС на 2 конгруэнтных отрезка. Расмотрим ? АВД. ? АВД прямоугольный , так как ВД перпендикулярно АС. Для то го чтобы найти 1 сторону прямоугольного треугольника.
Свойства прямоугольного треугольника
Прямоугольный треугольник — это геометрическая фигура, в которой один угол обязательно прямой. Треугольник с прямым углом имеет ряд свойств.
Основные свойства
Итак, свойства прямоугольного треугольника:
Первое и самое главное, прямой угол, благодаря которому он и получил свое название. Он, как известно, равен 90 градусам. Два остальных угла в сумме должны составлять также это значение. Таким образом, в обозначенной фигуре сумма всех углов должна составлять 180 градусов – это и есть свойства углов прямоугольного треугольника.
Второе, немаловажное свойство — это стороны прямоугольного треугольника: гипотенуза и два катета. Катет прямоугольного треугольника, что находится напротив угла в 30 градусов, равняется половине гипотенузы.
Теорема Пифагора
К свойствам прямоугольного треугольника относиться и теорема Пифагора: квадрат гипотенузы, равен суме квадратов катетов.
C 2 = a 2 + b 2 , где а и b – катеты, а с – гипотенуза.
Площадь прямоугольного треугольника равна половине произведения его катетов: S=1/2ab
Свойства медианы
Так же следует отметить и свойства медианы в прямоугольном треугольнике. Медианы, которые падают на гипотенузу, равны ее половине.
Если в прямоугольном треугольнике провести высоту с вершины, которая равна 90 о к гипотенузе, то треугольник делиться на два одинаковых прямоугольных треугольника. С этого можно сделать вывод, что высота в прямоугольном треугольнике, есть среднее геометрическое двух отрезков гипотенузы. Соответственно, каждый катет – среднее пропорциональное гипотенузы и смежных отрезков. Также нужно знать, что высота, которая опущена на гипотенузу, связана с катетами в соотношении: 1/а 2 + 1/b 2 = 1/f 2 , где а и b – катеты, а f –высота.
Напротив угла в 30 градусов лежит катет равный половине гипотенузы
Свойства прямоугольного треугольника
Прямоугольный треугольник — это геометрическая фигура, в которой один угол обязательно прямой. Треугольник с прямым углом имеет ряд свойств.
Основные свойства
Итак, свойства прямоугольного треугольника:
Первое и самое главное, прямой угол, благодаря которому он и получил свое название. Он, как известно, равен 90 градусам. Два остальных угла в сумме должны составлять также это значение. Таким образом, в обозначенной фигуре сумма всех углов должна составлять 180 градусов – это и есть свойства углов прямоугольного треугольника.
Второе, немаловажное свойство — это стороны прямоугольного треугольника: гипотенуза и два катета. Катет прямоугольного треугольника, что находится напротив угла в 30 градусов, равняется половине гипотенузы.
Теорема Пифагора
К свойствам прямоугольного треугольника относиться и теорема Пифагора: квадрат гипотенузы, равен суме квадратов катетов.
C 2 = a 2 + b 2 , где а и b – катеты, а с – гипотенуза.
Площадь прямоугольного треугольника равна половине произведения его катетов: S=1/2ab
Свойства медианы
Так же следует отметить и свойства медианы в прямоугольном треугольнике. Медианы, которые падают на гипотенузу, равны ее половине.
Если в прямоугольном треугольнике провести высоту с вершины, которая равна 90 о к гипотенузе, то треугольник делиться на два одинаковых прямоугольных треугольника. С этого можно сделать вывод, что высота в прямоугольном треугольнике, есть среднее геометрическое двух отрезков гипотенузы. Соответственно, каждый катет – среднее пропорциональное гипотенузы и смежных отрезков. Также нужно знать, что высота, которая опущена на гипотенузу, связана с катетами в соотношении: 1/а 2 + 1/b 2 = 1/f 2 , где а и b – катеты, а f –высота.
Напротив угла в 30 градусов лежит катет равный половине гипотенузы
Катет, лежащий против угла 30 градусов
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Проведем из вершины прямого угла медиану CF.
Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.
Следовательно, у него углы при основании равны:
Так как сумма углов треугольника равна 180º, то в треугольнике BFC
Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.
Значит, все его стороны равны и
Что и требовалось доказать.
Так как сумма острых углов прямоугольного треугольника равна 90º, то
Построим треугольник ADC, равный треугольнику ABC.
В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).
Следовательно, в треугольнике ABD все углы равны:
Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.

Похожие статьи
shtyknozh.ru
Построение углов на клетчатой бумаге — Математика, информатика, преподавание
Ключом к подобным «клетчатым» построениям углов является волшебное число 11. Если по клеткам нарисовать прямоугольный треугольник с одним катетом, равным 11 клеток, то выбор другого катета будет для этого треугольника давать следующие острые углы:
- 1 клетка — 5° и 85°
- 2 клетки — 10° и 80°
- 3 клетки — 15° и 75°
- 4 клетки — 20° и 70°
- 5 клеток — 25° и 65°
Запомнить нетрудно: каждая клетка добавляет по пять градусов, и так до пяти клеток. Погрешность составит около половины градуса для катетов 5 и 11 клеток, в остальных случаях она значительно меньше.
Ещё полезно помнить, что прямоугольный треугольник с катетами 8 и 11 клеток имеет острый угол 36° (с очень хорошей точностью). Это позволяет строить правильные пятиугольники и десятиугольники.
Волшебные свойства числа 11 на этом не заканчиваются. Выпишем последовательно натуральные числа: 3,4,5,6,7,8. Будем выбирать из них «крайние» пары: 3 и 8, 4 и 7, 5 и 6. Как видно, в сумме они все дают опять-таки 11. Если брать эти пары в качестве катетов, то получающиеся прямоугольные треугольники будут иметь следующие углы:
- 3 и 8 клеток — 20° и 70° (менее точно, чем для катетов 4 и 11 клеток)
- 4 и 7 клеток — 30° и 60°
- 5 и 6 — 40° и 50°
Ошибка составит около половины градуса для катетов 3 и 8 клеток, а в двух других случаях будет значительно меньше.
Отсюда следует способ построения по клеткам равностороннего треугольника: если взять горизонтальный или вертикальный отрезок 8 клеток и от его середины отступить в перпендикулярном направлении на 7 клеток, то получившийся равнобедренный треугольник будет практически равносторонним. Ошибка очень мала: для стандартной 5-мм клетки основание будет равно 4 сантиметра, а боковая сторона отличается от этой величины всего на 0.3 миллиметра. Это меньше, чем толщина карандашной линии.
Неплохо помнить ещё две пары катетов, дающих следующие острые углы:
- 2 и 9 клеток — 12° и 78°
- 1 и 10 клеток — 6° и 84°
Как видно, в сумме они составляют опять-таки 11. Наибольшая погрешность снова около половины градуса (у пары 2 и 9 клеток).
Эта клетчатая тригонометрия позволяет без проблем строить любые углы с шагом 5° без транспортира при неплохой точности.
blog.balandin.guru
Iteach
Материал из ИнтеВики — обучающей площадкой для проведения тренингов программы Intel
|
wiki.iteach.ru
Измерения и построение углов при проведении различных работ. Золотой египетский треугольник.
Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.
Угол 90 градусов.
Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол ( 90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.
А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.
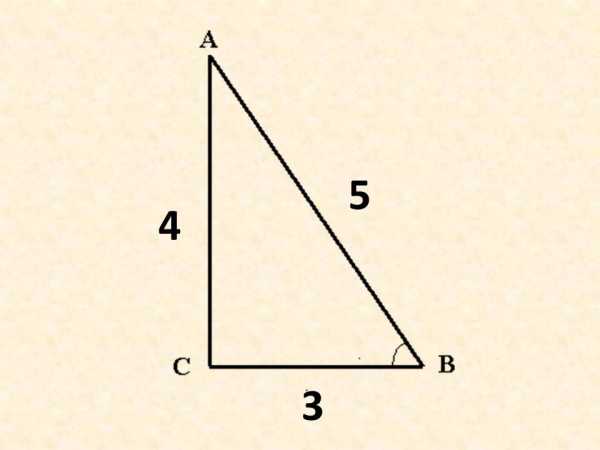
Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.
Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т.д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.
Угол 45 градусов.
Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.
Угол 30 и 60 градусов.
Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.
Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.
Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!
Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.
Прямоугольность заготовки.
При разметке заготовок или построений на деталях кроме самих углов весьма важно и их соотношение. Особенно это важно при изготовлении прямоугольных деталей или например при разметке фундамента, раскрое больших листов материала. Неправильное построение или разметка приносит впоследствии много лишней работы или к появлению большого числа отходов.
К сожалению, даже весьма точные разметочные инструменты, даже профессиональные, всегда имеют определенную погрешность.
Между тем, существует весьма простой метод определения прямоугольности детали или построения. В прямоугольнике диагонали абсолютно равны! Значит, после построения необходимо измерить длины диагоналей прямоугольника. Если они равны, все в порядке, это действительно прямоугольник. А если нет — вы построили параллелограмм или ромб. В этом случае следует немного «поиграть» смежными сторонами, что бы добиться точного (для данного случая) равенства диагоналей размечаемого прямоугольника.
К. Тимошенко
www.delaysam.ru
как построить угол без транспортира
Это ровно четвертинка от 90 градусов. Угол 90 град строится элементарно — как перпендикуляр к прямой. После чего остаётся дважды разделить его пополам. Для чего циркуль ставится в вершину угла, делаются засечки на двух сторонах угла, а потом тем же циркулем из этих засечек проводятся пересекающиеся дуги. Линия от точки их пересечения до вершину угла и есть биссектриса.
построй прямую, потом перпендикуляр к ней, потом подели угол в 90 на два, потом угол в 45 еще на два
циркулем поищи в нете как, а то много писать и надо рисовать. посмотри <a rel=»nofollow» href=»http://otvet.mail.ru/question/24858168/» target=»_blank» >здесь</a> как я понимаю тебе дали картинку? тогда тебе <a rel=»nofollow» href=»http://moodle.nci.kz/mod/resource/view.php?id=786″ target=»_blank» >сюда</a>
Нужно: Бумага, карандаш, линейка, циркуль, калькулятор Начертите одну из сторон угла. Для этого сначала поставьте точку, которая должна быть его вершиной, и обозначьте буквой А. Проведите начинающуюся от нее линию — сторону угла. 2 Постройте вспомогательный перпендикуляр к проведенной стороне. На бумаге в клеточку это сделать несложно, а для нелинованной бумаги и при отсутствии угольника можно воспользоваться циркулем. Этот метод удобен и для случаев, когда на бумаге в клеточку сторона угла расположена наклонно. Начертите два пересекающихся круга, центры которых лежат на стороне угла. Проведите прямую через точки пересечения окружностей — это и будет перпендикуляр. Точку его пересечения со стороной угла обозначьте буквой В. 3 Измерьте длину отрезка АВ. Полученное число будет участвовать в расчетах, поэтому желательно построить перпендикуляр на таком расстоянии от точки А, чтобы число было круглым — это упростит вычисления. 4 Отложите на перпендикуляре расстояние, которое равно произведению полученного на предыдущем шаге числа на тангенс нужного угла. Для вычисления тангенса воспользуйтесь таблицами тригонометрических функций или калькулятором — например, встроенным в операционную системы программным калькулятором. Скажем, если длина отрезка АВ равна 20 см, а начертить нужно угол в 55°, то на перпендикуляре надо отложить 20*tg(55°)≈20*tg(55°)≈20*1,428=28,56 см. 5 Вместо тангенса можно использовать другую тригонометрическую функцию — например, если вы выберете косинус, длину отрезка АВ надо делить на косинус нужного угла. Но в этом случае вы получите длину второй стороны угла, а точку ее примыкания к перпендикуляру надо будет определять с помощью циркуля. Для примера из предыдущего шага вычисления в этом случае будут выглядеть так: 20/cos(55°)≈20/0,576≈34,72 см. Полученную величину отложите на циркуле, установите его в вершину угла и отметьте на перпендикуляре точку его пересечения с воображаемой окружностью отложенного радиуса. 6 Отмерив на перпендикуляре одним из описанных способов отрезок нужной длины, поставьте точку и обозначьте ее буквой С. Затем начертите вторую сторону угла — соедините его вершину (точку А) с точкой С. На этом построение угла ВАС будет завершено.
touch.otvet.mail.ru
Построение острых углов на клетчатой бумаге
Геометрия – часть математики, изучающая пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре. Происхождение термина «геометрия» с греческого означает «землемерие» [гео– «земля» и метрео – «измеряю»].
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Углы измеряются в градусах и радианах. Угол, образованный продолжением сторон данного угла, называется вертикальным к данному. Угол, образованный одной из сторон данного угла и продолжением другой стороны, называется смежным с ним. Приспособление для построения углов на чертежах, называется транспортир.
Значение геометрии в развитии математике
Применение евклидовой геометрии представляет самое обычное явление всюду, где определяются площади, объемы и т. п. Геометрия изучает пространственную непрерывность. Общая роль геометрии в математике состоит также в том, что с нею связано идущее от пространственных представлений точное синтетическое мышление, часто позволяющее охватить в целом то, что достигается анализом и выкладками лишь через длинную цепь шагов. Геометрия характеризуется не только своим предметом, но и методом, идущим от наглядных представлений и оказывающимся плодотворным в решении многих проблем других областей математики. Геометрия имела решающее значение в возникновении и развитии анализа. Интегрирование происходит от нахождения площадей и объемов. Графическое представление функций сыграло важную роль в выработке понятий анализа и сохраняет свое значение. Геометрия оказывает влияние на алгебру, и даже на арифметику – теорию чисел, поэтому роль геометрии в развитии математике очень велика.
Цель работы: найти способ построения углов без транспортира.
Гипотеза: Любой острый угол можно построить без транспортира по узлам клетки.
Задачи:
• рассмотреть углы и найти их связь с узлами клеток.
Построим с помощью транспортира углы от 10° до 80° со стороной, идущей по горизонтальной линии сетки.
Отметим у каждого угла ближайший узел сетки, через который прошла другая сторона каждого угла.
Определим «путь» из вершины угла в отмеченную точку и занесем данные в таблицу:
Величина угла Клеток → Клеток ↑
10° 6 1
20° 8 3
30° 7 4
40° 6 5
50° 5 6
60° 4 7
70° 3 8
80° 1 6
Если сравнить данные таблицы для углов 10° и 80°, 20° и 70°, 30° и 60°, 40° и 50°, то можно заметить, что количество клеток вправо и количество клеток вверх меняются местами.
Используя данные таблицы, можно приближенно построить любой острый угол без транспортира.
Заключение
Таким образом, обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур. В 7 классе мы начинаем изучать геометрию и, полученными результатами, можно будет пользоваться при изучении курса планиметрии для построения схематических чертежей, точнее соответствующих условию задач.
Также, выполняя презентацию работы, я совершенствовала свои навыки работы на компьютере.
www.hintfox.com
Как сделать угол 75 градусов без транспортира?
Ширина 1 клеточки, высота — 4, вроде это соотношение правильное. А без клеточек ни как 😉
Чертежными угольниками: 45 + 30.
90 градусов — пополам, из второй половины добавить 2/3. все конечно приблизительно
по клеточкам. В прямоугольнике 5*3 проводишь диагональ — это составляет 30 градусов с большей стороной, и вниз проводишь по диагонали квадрата по клеточкам прямую — это 45. 30+45 = 75
Если надо построить угол на местности, то возьмите шнур, рулетку, и калькулятор с арктангенсами.
75 = 60+15 = 60+60/2/2 Угол в 60 градусов строятся циркулем и линейкой понятно как. Разделить угол пополам циркулем и линейкой тохе не штука. И потом не штука отложить угол, равный данному, от второй стороны угла в 60 градусов.
touch.otvet.mail.ru
